Java 基本数据类型

基本数据类型	字节数	位数	默认值	取值范围	描述
byte	1	8	0	[2^7-1, -2^7]	整型
short	2	16	0	[2^15-1, -2^15]	整型
int	4	32	0	[2^31-1, -2^31]	整型
long	8	64	0L	[2^63-1, -2^63]	长整型
float	4	32	0f	[2^31-1, -2^31]	单精度浮点型
double	8	64	0d	[2^63-1, -2^63]	双精度浮点型
char	2	16	‘u0000’	[0, 2^16]	字符型
boolean	1		false	-	布尔型

浮点型数据精度

• 计算精度针对的是浮点型数，整型数不存在计算精度的问题。

• 精算精度问题针对的是浮点型数据类型在计算时发生精度丢失的问题。

为什么会出现精度问题 ？

结论： 计算机 CPU 只认识二进制数 0 和 1，十进制与二进制转换时造成浮点数精度的根本原因。

先看一个例子🌰：

public static void main(String[] args) {
    float a = 1f;
    float b = 0.9f;
    float c = 0.1f;

    System.out.println(b + c);            // 1.0
    System.out.println((b + c) == a);     // true

    System.out.println(a - b);            // 0.100000024
    System.out.println((a -b) == c);      // false
}

浮点数十进制转二进制

浮点数十进制转二进制分为两部分，整数部分和小数部分。

整数部分：除二取余，倒叙排列的方式计算；

小数部分：乘二取整，顺序排列的方式计算；

举个例子🌰： 0.9f

正数：首位(从左向右-符号位)为 0

正数部分：0

小数部分：0.11100110011001100110011001100110011001100110011001101

我们发现0.9的小数部分是 1100 死循环的，但是寄存器存放数字的长度是有限的，超出的部分就会被计算器丢弃，这也就是精度丢失的根本原因。

浮点数在计算机中存储形式

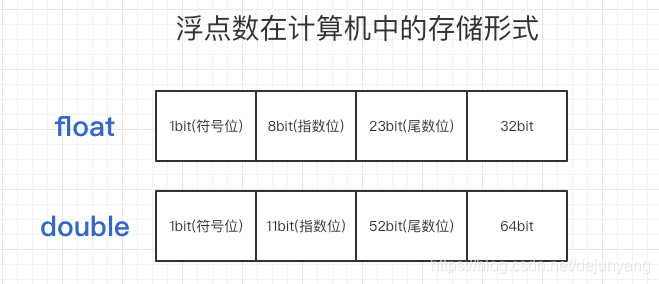
符号位：0为正，1为负；