代码随想录算法训练营第二十三天 | 39.组合总和 40.组合总和Ⅱ 131.分割回文串

最新推荐文章于 2025-11-25 11:31:36 发布

原创最新推荐文章于 2025-11-25 11:31:36 发布 · 988 阅读

14 ·

CC 4.0 BY-SA版权

文章标签：

#算法

小tips：

回溯的题目，先思考清晰对应二叉树的节点和孩子节点很有帮助

LeetCode 39.组合总和：

文章链接
题目链接：39.组合总和

思路：

分析题目：① 只要和为target，就可以，不限制组合中元素个数，因此树的深度不限
② 同一个元素可以被重复选取，因此递归到下一层可以选择之前层的元素。
如下图所示，红色部分是不符合条件的部分
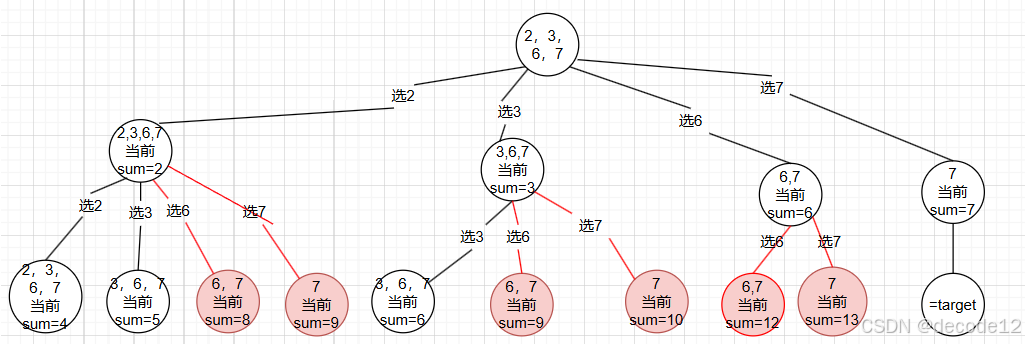
在这里插入图片描述
① 传入参数为candidates，startIndex(因为是在同一集合中求组合)，target记录目标数(为0表示达到目标)，path记录路径
② 边界条件：target <= 0。target=0表示找到了一个符合条件的组合；target < 0找到的组合超出了目标，不符合条件
③ 遍历：for循环的区间为[startIndex, len(candidates))，递归时传入的startIndex为for循环中的序号 i ，不是 i + 1(因为可重复)
可添加剪枝：对列表排序后进行剪枝，根据上图可知，只要candidates[i] > target(也可以是sum + candidates[i] > target)时，可以直接连同后面一起剪枝

class Solution:
    def combinationSum(self, candidates: List[int], target: int) -> List[List[int]]:
        candidates.sort()
        self.result = []
        self.backtracking(candidates, 0, target, [])
        return self.result

    def backtracking(self, candidates, startIndex, target, path):   
        if target <= 0:
            if target == 0:
                self.result.append(path[:])
            return
        for i in range(startIndex, len(candidates)):
            if candidates[i] > target:
                break
            path.append(candidates[i])
            self.backtracking(candidates, i, target - candidates[i], path)
            path.pop()

LeetCode 40.组合总和Ⅱ：

文章链接
题目链接

思路：

分析题目得到：1）list中的元素每个组合中只能使用一次 2）list中的元素可能重复，比如[1, 1, 2]这样
先对list排序，再进行回溯，目的是让相同的元素位于相邻的位置，且sum + candidates[a] > target时可以直接剪枝i >= a 的全部枝条
如果按照之前的遍历方式会得到如下树，因为list中的元素可能重复，所以遍历后会出现重复的组合，从而需要去重。
下图中紫色部分为重复部分，需要去重（算广义上的剪枝）；红色部分为sum + candidates[i] > target部分，需要剪枝。（一般剪枝默认为去掉不符合条件的组合，重复部分可能出现符合条件的组合，但是由于重复了，因此也需要剪枝）
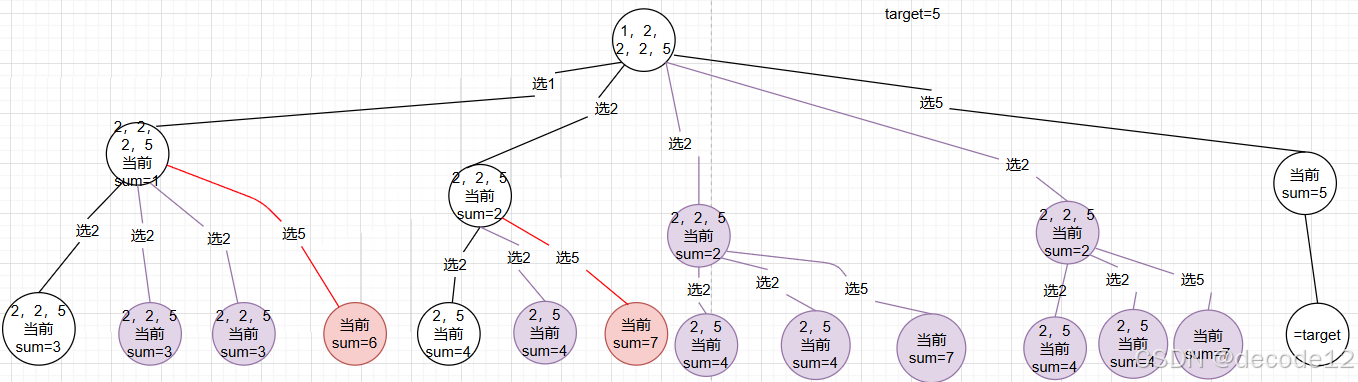
在这里插入图片描述

剪枝部分：
剪枝部分一般都是在递归的for循环中进行修剪:
1）去重：条件为 i > startIndex因为去重只在本循环中去（去重部分举例理解为，list中存在[1, 2, 2, 2, 5]，在树的第二层将第一个2的合法组合都得到之后，后面重复的2的合法组合实际上与第一个2重复了，因此剪去）。缺少该条件的话，就变成了采用 list 中不重复的元素进行组合，也就是剪去了下图中的蓝色合法部分。通俗理解就是剪去了[1,2,2]这一组合。

if i > startIndex and candidates[i] == candidates[i - 1]:
	continue

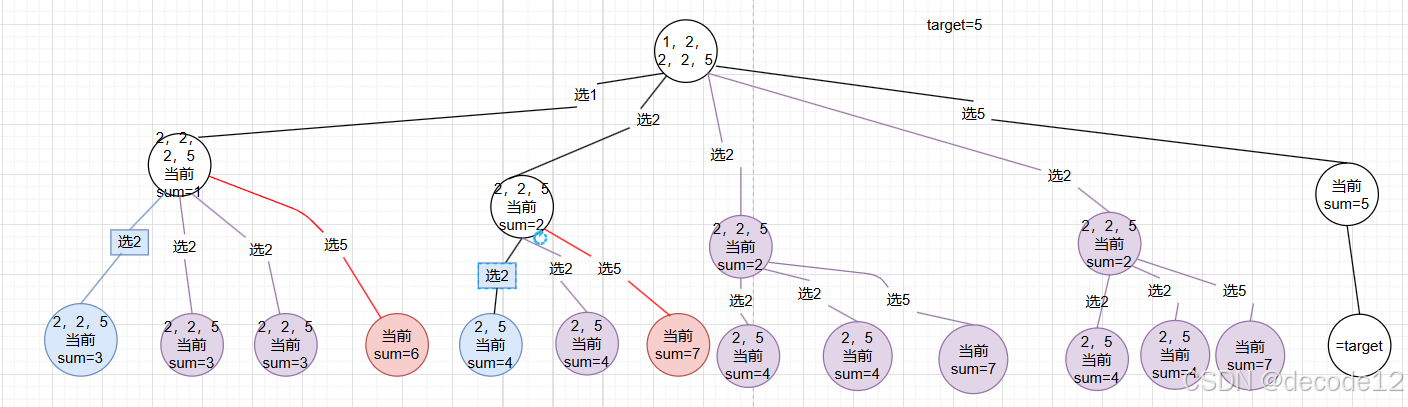
在这里插入图片描述
2）剪枝：

if candidates[i] > target：
	break

注意，两个剪枝剪的部分不同，去重是continue，只剪去自己这一支，第二个剪枝是break，剪去自己和之后的全部枝条

class Solution:
    def combinationSum2(self, candidates: List[int], target: int) -> List[List[int]]:
        candidates.sort()
        self.result = []
        self.backtracking(candidates, 0, target, [])
        return self.result

    def backtracking(self, candidates, startIndex, target, path):
        if target <= 0:
            if target == 0:
                self.result.append(path[:]) # 记得添加的是path的复制，如果append(path)添加的是path的引用
            return
        for i in range(startIndex, len(candidates)):
            if candidates[i] > target:  # 后面全部剪枝
                break
            # 去重，i > startIndex而不是 i > 0，因为只是在当前层的遍历中去重
            if i > startIndex and candidates[i] == candidates[i - 1]:   
                continue
            path.append(candidates[i])
            self.backtracking(candidates, i + 1, target - candidates[i], path) # 每个数字只能取一次
            path.pop()

感悟：

本道题需要注意的部分比较多：去重和剪枝，去重是在递归的for循环中去重。同时要注意细节：回溯前 list 需要排序，result添加的是path的复件而不是引用，两个剪枝剪去的部分不同，一个是continue只剪当前，一个是break剪去当前和之后。

LeetCode 131.分割回文串：

文章链接
题目链接：131.分割回文串

思路：

首先明确对应的二叉树如何构造，二叉树构造如下，其中红色部分是切割错误的部分。因此分割回文串实际上就是先确定第一个部分的结尾，然后递归切割后面的字符串，同时切割时要确定是否为回文串。
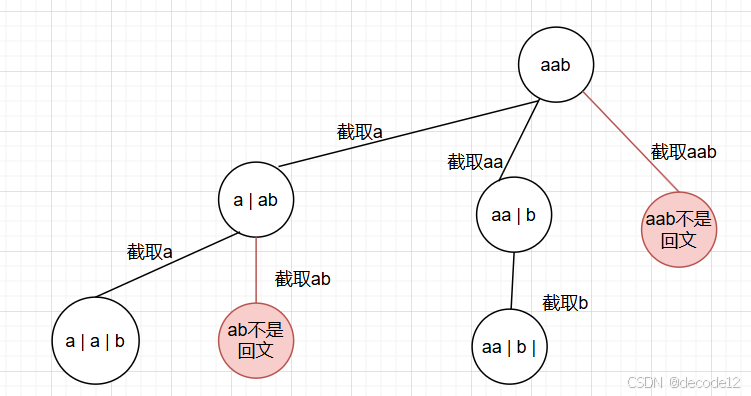
在这里插入图片描述

回溯：

① 参数：字符串s， left要切割部分开始，right要切割部分结束（实际上只在判断要切割字符串是否为空起作用，可以不用），path记录路径
② 边界条件：要切割的字符串为空。如果是判断要切割的字符串为一个字符也可以（需要在判断中增加path.append(s[left:right])且字符串是否为空也要判断）
③ 遍历：for循环遍历的是当前字符串第一个切割部分的尾部，区间为[left, right]，同时需要判断是否为回文串。

判断是否为回文串：

双指针
动态规划
$\begin{cases} & d[i+1][j-1] and \ s[i] == s[j] &,else \\ & s[i] == s[j] &, j - i = 1（只有两个字符） \\ & = True &, i = j（只有一个字符） \end{cases}$

"""
回溯 + 双指针判断回文
"""
class Solution:
    def partition(self, s: str) -> List[List[str]]:
        self.result = []
        self.backtracking(s, 0, len(s) - 1, [])
        return self.result

    def palindrome(self, s, left, right):
        i, j = left, right  # 双闭区间
        while i < j and s[i] == s[j]:
            i += 1
            j -= 1
        if i >= j:
            return True
        else:
            return False
    def backtracking(self, s, left, right, path):
        if left > right:    # 双闭区间
            self.result.append(path[:]) 
            return
        for j in range(left, right + 1):    # j为切分当前字符串第一个部分的尾部
            if self.palindrome(s, left, j):
                path.append(s[left: j + 1])
                self.backtracking(s, j + 1, right, path)
                path.pop()

"""
回溯 + 动态规划判断回文
"""
class Solution:
    def partition(self, s: str) -> List[List[str]]:
        self.result = []
        self.palindrome = self.computePalindrome(s)
        self.backtracking(s, 0, len(s) - 1, [])
        return self.result

    def computePalindrome(self, s):
        palindrome = [[False] * len(s) for _ in range(len(s))]
        for i in range(len(s) - 1, -1, -1):
            for j in range(i, len(s)):
                if i == j:  # 只有一个元素
                    palindrome[i][j] = True
                elif i == j - 1:    # 只有两个元素
                    palindrome[i][j] = (s[i] == s[j])
                else:
                    palindrome[i][j] = (palindrome[i + 1][j - 1] and (s[i] == s[j]))
        return palindrome

    def backtracking(self, s, left, right, path):
        if left > right:    # 双闭区间  实际上right只在这里用到了，可以换成left > len(s) - 1
            self.result.append(path[:]) 
        for j in range(left, right + 1):    # j为切分当前字符串第一个部分的尾部
            if self.palindrome[left][j]:
                path.append(s[left: j + 1])
                self.backtracking(s, j + 1, right, path)
                path.pop()

    
"""
边界条件为单个字符
"""   
class Solution:
    def partition(self, s: str) -> List[List[str]]:
        self.result = []
        self.palindrome = self.computePalindrome(s)
        self.backtracking(s, 0, len(s) - 1, [])
        return self.result

    def computePalindrome(self, s):
        palindrome = [[False] * len(s) for _ in range(len(s))]
        for i in range(len(s) - 1, -1, -1):
            for j in range(i, len(s)):
                if i == j:  # 只有一个元素
                    palindrome[i][j] = True
                elif i == j - 1:    # 只有两个元素
                    palindrome[i][j] = (s[i] == s[j])
                else:
                    palindrome[i][j] = (palindrome[i + 1][j - 1] and (s[i] == s[j]))
        return palindrome

    def backtracking(self, s, left, right, path):
        if left >= right:    # 单个字符和空都要判断
            if left == right:
                path.append(s[left:right + 1])
                self.result.append(path[:]) 
                path.pop()
            else:
                self.result.append(path[:])
            return
        for j in range(left, right + 1):    # j为切分当前字符串第一个部分的尾部
            if self.palindrome[left][j]:
                path.append(s[left: j + 1])
                self.backtracking(s, j + 1, right, path)
                path.pop()