攻防世界crypto部分Handicraft_RSA的writeup

有人正在他老房子的地下室里开发自己的RSA系统。 证明他这个RSA系统只在他的地下室有效！

1、下载文件丢到kali里看看是啥文件：

提示是XZ文件，解压得一个同名的文件，用editplus打开，发现是一个加密过程。里面有公钥和加密后的文本。

2、将公钥保存成pub.pem用rsactftool生成私钥：

python3 ~/RsaCtfTool/RsaCtfTool.py --publickey pub.pem --private

3、将私钥保存成private.pem，然后进行多次RSA解密，因为我也不知道加密了多少次，所以用了100次循环来解密，代码如下：

from Crypto.PublicKey import RSA
import base64
with open('private.pem') as f:
    p = f.read()
    rsakey = RSA.importKey(p)
    private_key = RSA.construct((int(rsakey.n), int(rsakey.e), int(rsakey.d)))

msg= base64.b64decode("eER0JNIcZYx/t+7lnRvv8s8zyMw8dYspZlne0MQUatQNcnDL/wnHtkAoNdCalQkpcbnZeAz4qeMX5GBmsO+BXyAKDueMA4uy3fw2k/dqFSsZFiB7I9M0oEkqUja52IMpkGDJ2eXGj9WHe4mqkniIayS42o4p9b0Qlz754qqRgkuaKzPWkZPKynULAtFXF39zm6dPI/jUA2BEo5WBoPzsCzwRmdr6QmJXTsau5BAQC5qdIkmCNq7+NLY1fjOmSEF/W+mdQvcwYPbe2zezroCiLiPNZnoABfmPbWAcASVU6M0YxvnXsh2YjkyLFf4cJSgroM3Aw4fVz3PPSsAQyCFKBA==")

with open('decode.txt', 'w+') as f:
    for s in range(1,100):
        msg = private_key.decrypt(msg)
        f.write(repr(msg) + '\n')

4、查看生成的decode.txt，即可看见flag：

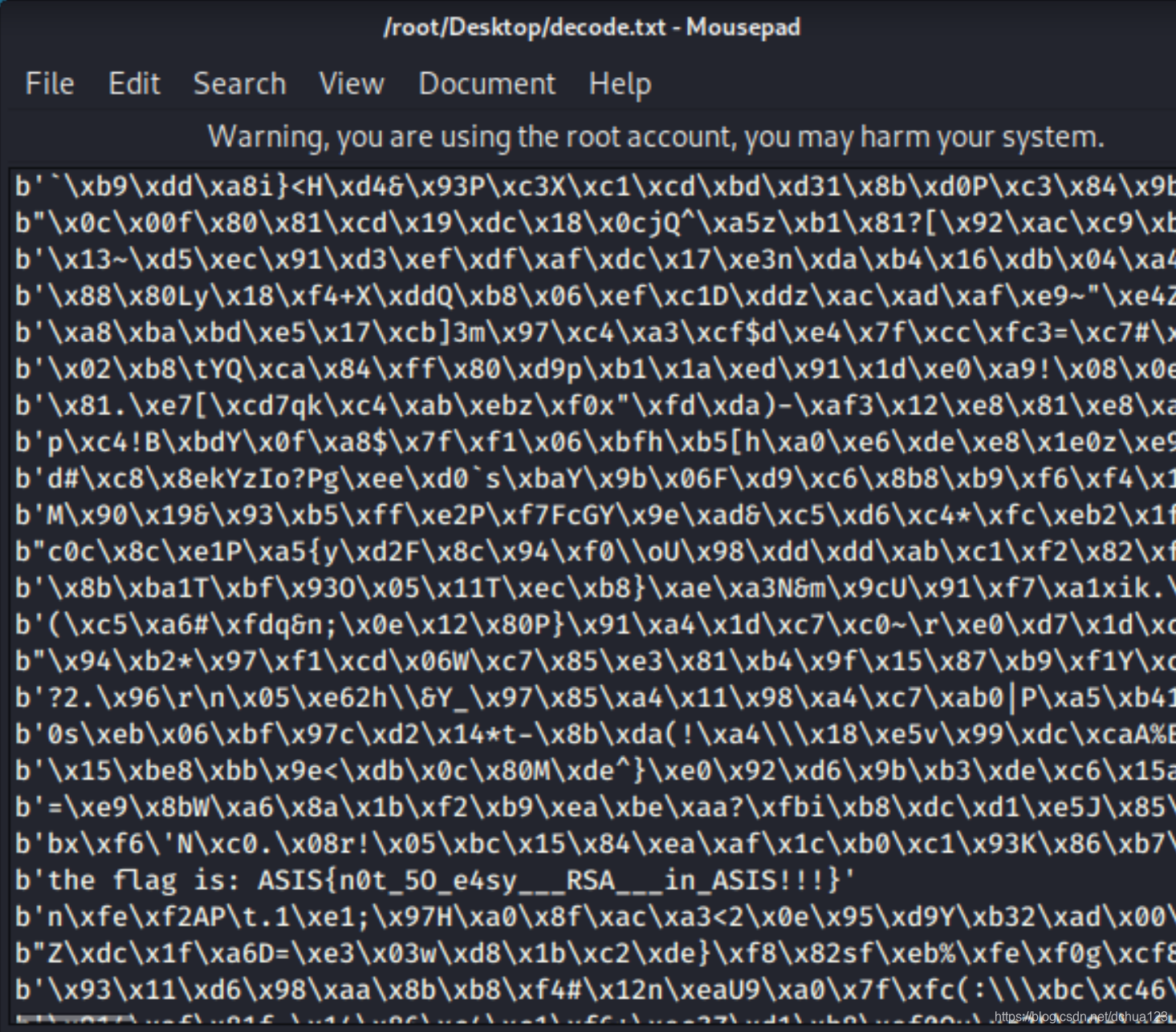
flag即是：

ASIS{n0t_5O_e4sy___RSA___in_ASIS!!!}