通俗解释:SGD 随机梯度下降优化器
SGD(Stochastic Gradient Descent) 就像一个“摸着石头过河”的探险家,每次只根据脚下的一小块石头(一个样本或小批量样本)调整方向,快速找到下山的最优路径(最小化损失函数)。
核心思想
-
传统梯度下降(BGD)的缺点
-
想象你站在山顶,想找到最快下山的路。
-
BGD 会先测量整座山所有点的坡度(计算全量梯度),再决定迈哪一步。优点是方向准,缺点是耗时(计算量大)。
-
-
SGD 的改进
-
SGD 每次只踩一块石头(随机选一个样本),根据这块石头的坡度(单样本梯度)迈步。
-
优点:计算快,适合大数据;缺点:可能被一块大石头误导(噪声大),走弯路。
-
SGD 的工作流程
-
随机选样本:从数据集中随机挑一个样本(或一小批样本)。
-
算梯度:根据这个样本计算当前参数的梯度(坡度)。
-
更新参数:沿着梯度的反方向(下山方向)调整参数。
-
重复:不断选新样本,直到参数稳定(损失函数不再明显下降)。
公式:
-
θ:模型参数(比如直线的斜率和截距)
-
η:学习率(步长,决定每次迈多大)
-
∇L(θt):当前样本的梯度(坡度)
举个实际例子
假设你训练一个模型预测房价(y=wx+b):
-
初始参数:随机猜 w=2, b=1(可能预测不准)。
-
随机选一个样本:比如房子面积 x=3,实际价格 y=7。
-
计算梯度:当前预测值 y^=2×3+1=7,误差为0,梯度为0 → 参数不变。
-
再选一个样本:x=4,实际 y=9。预测值 y^=2×4+1=9,误差仍为0 → 参数不变。
-
继续迭代:多次随机采样后,参数逐渐逼近真实值(比如 w=1.8, b=2.5)。
SGD 的优缺点
| 优点 | 缺点 |
|---|---|
| 计算快:单样本计算,适合大数据 | 噪声大:单样本梯度可能误导方向 |
| 跳出局部最优:随机性可能找到更好的全局最优 | 需调学习率:步长太大易震荡,太小收敛慢 |
| 内存友好:不需要存全量数据梯度 | 收敛慢:需更多迭代次数 |
SGD 的“智能升级版”
纯SGD太“莽撞”,实际中常结合其他技巧:
-
Mini-batch SGD:每次用一小批样本(如32个),平衡效率与稳定性。
-
动量法(Momentum):记住之前的移动方向,减少震荡。
-
自适应学习率:如Adam优化器,自动调整步长。
总结
SGD 是深度学习的“基石优化器”,通过随机采样+快速迭代,在大数据场景下高效训练模型。虽然它有点“近视”(只看局部),但通过技巧(如动量、学习率调整)可以变得聪明,最终找到最优解。




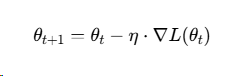

















 4061
4061

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










