剑指 Offer II 008. 和大于等于 target 的最短子数组

最新推荐文章于 2025-12-22 09:47:08 发布

原创最新推荐文章于 2025-12-22 09:47:08 发布 · 95 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #leetcode #数据结构

文章介绍了两种方法来解决寻找数组中满足特定条件的最小子串长度问题。第一种方法使用滑动窗口，时间复杂度为O(n)，空间复杂度为O(1)。第二种方法利用二分法和前缀和，时间复杂度为O(nlogn)，空间复杂度为O(n)。两种方法都在C++中实现，通过比较和调整左右指针或进行二分查找找到符合条件的子串。

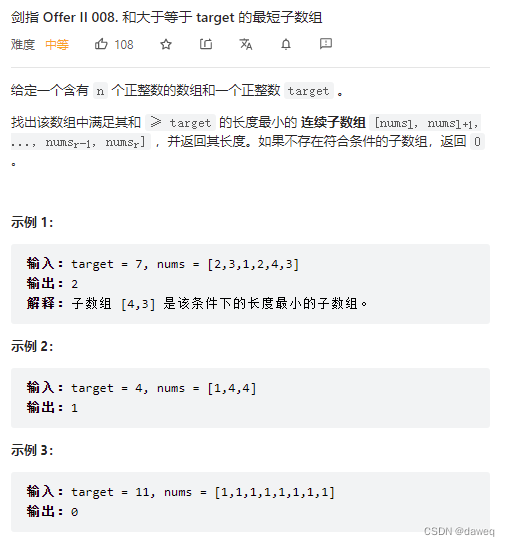
在这里插入图片描述
思路：
（1）因为这道题要遍历子串来获得对应得子串长度，所以考虑滑动窗口时最直接得思路
时间复杂度：O(n)，
空间复杂度：O(1)。

（2）因为没有负数，也可以采用二分法
时间复杂度：O(nlogn)，
空间复杂度：O(n)。

（1）滑动窗口
这里得主要代码思路就是右指针不停在走，一直到第一次满足条件。之后左指针走，并逐步删除左边的元素，知道不满足条件后，右指针向右走，这样就能达到遍历符合要求的子串的效果了。

class Solution {
public:
    int minSubArrayLen(int target, vector<int>& nums)
    {
        int low = 0;
        int high = 0;
        int res=INT_MAX;
        int sum = 0;
        int len = nums.size();
        for (high;high < len;high++)
        {
            sum += nums[high];
            while (low <= high && sum >= target)
            {res = min(res, high - low + 1);
            sum -= nums[low++];
        }
        }
        return res == INT_MAX ? 0 : res;
    }
};

（2）二分法
sums保存的是累计和，比如sums[2]表示nums前两个数据的和。lower_bound是现成的库和函数来为我们实现这里二分查找大于等于某个数的第一个位置的功能。

class Solution {
public:
    int minSubArrayLen(int s, vector<int>& nums) {
        int n = nums.size();
        if (n == 0) {
            return 0;
        }
        int ans = INT_MAX;
        vector<int> sums(n + 1, 0);
        // 为了方便计算，令 size = n + 1 
        // sums[0] = 0 意味着前 0 个元素的前缀和为 0
        // sums[1] = A[0] 前 1 个元素的前缀和为 A[0]
        // 以此类推
        for (int i = 1; i <= n; i++) {
            sums[i] = sums[i - 1] + nums[i - 1];
        }
        for (int i = 1; i <= n; i++) {
            int target = s + sums[i - 1];
            auto bound = lower_bound(sums.begin(), sums.end(), target);
            if (bound != sums.end()) {
                ans = min(ans, static_cast<int>((bound - sums.begin()) - (i - 1)));
            }
        }
        return ans == INT_MAX ? 0 : ans;
    }
};