CART决策树

CART简介

CART算法采用二分递归分割的技术将当前样本集分为两个子样本集，使得生成的每个非叶子节点都有两个分支。非叶子节点的特征取值为True和False，左分支取值为True，右分支取值为False，因此CART算法生成的决策树是结构简洁的二叉树。CART可以处理连续型变量和离散型变量，利用训练数据递归的划分特征空间进行建树，用验证数据进行剪枝。

• 如果待预测分类是离散型数据，则CART生成分类决策树。
• 如果待预测分类是连续性数据，则CART生成回归决策树。

CART分类树

描述不确定性可以使用熵也可以使用基尼指数。同熵，基尼指数越大，样本集合的不确定性越大。
假设有$K$个类，样本点属于第$k$个类的概率为$p_k$，则概率分布的基尼指数定义为
$$Gini(p)=\sum _{k=1}^K{p}_k(1-p_k)=1-\sum _{k=1}^K{p}_k^2$$
根据基尼指数定义，可以得到样本集合$D$的基尼指数，其中$C_k$表示数据集$D$中属于第$k$类的样本子集。
$$Gini(D)==1-\sum _{k=1}^K{\left(\frac{|C_k|}{|D|}\right)}^2$$
如果数据集$D$根据特征$A$在某一取值$a$上进行分割，得到$D1,D2$两部分后，那么在特征$A$下集合$D$的基尼系数如下所示。
$$Gini(D,A)=\frac{|D1|}{D}Gini(D1)+\frac{|D2|}{D}Gini(D2)$$
其中基尼系数$Gini(D)$表示集合$D$的不确定性，基尼系数$Gini(D,A)$表示$A=a$分割后集合$D$的不确定性。
依据信息增益，决策树构建应该是选择最大的信息增益，首先选择最优分割点，即
$$\underset{a\in A}{\max }(Gini(D)-Gini(D,A))$$
再然后，选择最优分割属性
$$\underset{A\in Attribute}{\max }(\underset{a\in A}{\max }(Gini(D)-Gini(D,A)))$$
由于针对当前步计算时Gini(D)为固定值，所以以上可以改写为
$$\begin{gathered} \underset{a\in A}{\min }Gini(D,A) \\ \underset{A\in Attribute}{\min }(\underset{a\in A}{\min }Gini(D,A)) \end{gathered}$$
实例参考：https://blog.youkuaiyun.com/ExtraMan/article/details/41744003

CART回归树

CART回归树预测回归连续型数据，假设$X$与$Y$分别是输入和输出变量，并且$Y$是连续变量。即
D = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , ⋯   , ( x n , y n ) } D = \{(x_1,y_1),(x_2,y_2),\cdots,(x_n,y_n)\} D={(x1​,y1​),(x2​,y2​),⋯,(xn​,yn​)}

• 在训练数据集所在的输入空间中，递归的将每个区域划分为两个子区域并决定每个子区域上的输出值，构建二叉决策树。
• 选择最优切分变量$j$(属性)与切分点$s$(值)：遍历变量$j$，对规定的切分变量$j$扫描切分点$s$，选择使下式得到最小值时的$(j,s)$对。其中$R$是被划分的输入空间，$c$是空间$R$对应的固定输出值。
  
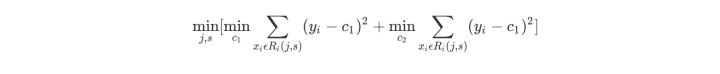
  对于$Gini(D,A)$当分布较均匀时（或数据稳定时），值会小，类比于上式的方差（方差也是描述数据的稳定性）
• 用选定的$(j,s)$对，划分区域并决定相应的输出值
  
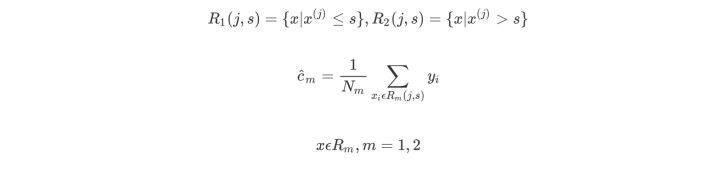
• 继续对两个子区域调用上述步骤，将输入空间划分为$M$（为树的叶子节点数）个区域$R_1,R_2,\cdots ,R_M$，生成决策树，$I$返回0或1。（某个输入只能对应到一个叶子节点，这个地方的理解可能有问题）
  
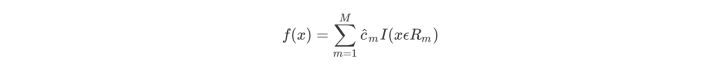
  实例参考：
  1.https://www.cnblogs.com/limingqi/p/12421960.html
  2.https://blog.youkuaiyun.com/huahuaxiaoshao/article/details/86183738