[剑指offer]面试题第[49]题[Leetcode][第264题][JAVA][丑数][动态规划][堆]

最新推荐文章于 2024-07-21 05:52:26 发布

CryptWinter

最新推荐文章于 2024-07-21 05:52:26 发布

阅读量234

点赞数

CC 4.0 BY-SA版权

分类专栏：非0即1 刷题文章标签： java 动态规划 leetcode 剑指offer

本文链接：https://blog.youkuaiyun.com/dadongwudi/article/details/107427104

刷题同时被 2 个专栏收录

249 篇文章

订阅专栏

非0即1

239 篇文章

订阅专栏

本文深入解析了求解第N个丑数的两种高效算法：动态规划和优先队列（堆）。动态规划方法通过状态转移方程递推计算，实现O(N)的时间复杂度和空间复杂度。而堆方法则利用优先队列和哈希集合进行去重，同样达到O(N)的时间复杂度，但空间复杂度更优。文章提供了清晰的代码示例和步骤解释。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

【问题描述】[中等]

【解答思路】

1. 动态规划

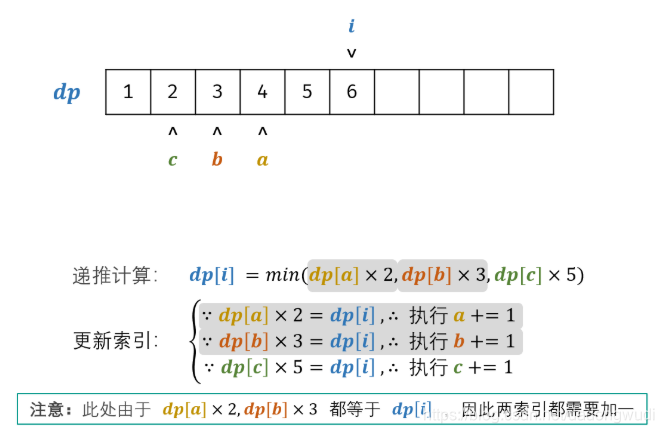
在这里插入图片描述

时间复杂度：O(N) 空间复杂度：O(N)
在这里插入图片描述

class Solution {
    public int nthUglyNumber(int n) {
        int a = 0, b = 0, c = 0;
        int[] dp = new int[n];
        dp[0] = 1;
        for(int i = 1; i < n; i++) {
            int n2 = dp[a] * 2, n3 = dp[b] * 3, n5 = dp[c] * 5;
            dp[i] = Math.min(Math.min(n2, n3), n5);
            if(dp[i] == n2) a++;
            if(dp[i] == n3) b++;
            if(dp[i] == n5) c++;
        }
        return dp[n - 1];
    }
}

作者：jyd
链接：https://leetcode-cn.com/problems/chou-shu-lcof/solution/mian-shi-ti-49-chou-shu-dong-tai-gui-hua-qing-xi-t/

2. 堆

在这里插入图片描述

时间复杂度：O(N) 空间复杂度：O(1)

class Solution {
    public int nthUglyNumber(int n) {
        PriorityQueue<Long> pq = new PriorityQueue<>();
        Set<Long> s = new HashSet<>();
        //初始化,放进堆和set，发现1要开Long数组才可以
        long[] primes = new long[]{2, 3, 5};
        for (long prime : primes) {
            pq.offer(prime);
            s.add(prime);
        }
        long num = 1;
        for (int i = 1; i < n; i++) {
            num = pq.poll();
            //遍历三个因子
            for (int j = 0; j < 3; j++) {
                if (!s.contains(num * primes[j])) {
                    pq.offer(num * primes[j]);
                    s.add(num * primes[j]);
                }
            }
        }
        return (int) num;
    }
}

作者：jerry_nju
链接：https://leetcode-cn.com/problems/chou-shu-lcof/solution/dui-he-dong-tai-gui-hua-si-lu-xiang-jie-by-jerry_n/

【总结】

1.动态规划流程

第 1 步：设计状态
第 2 步：状态转移方程
第 3 步：考虑初始化
第 4 步：考虑输出
第 5 步：考虑是否可以状态压缩

2.优先队列按大小弹出溢出问题long 去重set

参考链接：
https://leetcode-cn.com/problems/chou-shu-lcof/solution/dui-he-dong-tai-gui-hua-si-lu-xiang-jie-by-jerry_n/
参考链接：https://leetcode-cn.com/problems/chou-shu-lcof/solution/mian-shi-ti-49-chou-shu-dong-tai-gui-hua-qing-xi-t/