【数据结构】------回溯法实现迷宫问题

我们先来了解下回溯法，什么是回溯法？

回溯法：对于一个包括有很多个结点，每个结点有若干个搜索分支的问题，把原问题分解为若干子问题求解的算法；当搜索到某个结点发现无法再继续搜索下去，就让搜索过程（回溯）回退到该节点的前一个节点，继续搜索该节点外的其他尚未搜索的分支；如果发现该结点无法再继续进行搜索下去的时候，就让搜索过程回溯到这个结点的前一结点继续这样的搜索过程，这样的搜索过程一直进行到搜索到问题的解或者搜索完了全部可搜索的分支没有解存在为止。

简单迷宫
我们首先得创建出来的是一张地图，展示我们实现迷宫的过程。我们用0来标记此路不通，用1来标记此路可以走，我们用2来标记走过的路。我们默认的是出口点和入口点都是边界上的点，并且出口不可能和入口是同一点，那么我们的实现就没有意义了，其次要想将自己走过的路的坐标位置压入到栈中，如果这条路我们可以继续往下走，那么我们就一直入栈，直到我们走到出口，如果我们走的下一点不通，就将该点进行出栈操作，然后对该点的四面进行扫描。继续找可以通的点。依次进行循环，直到我们能找到适合自己的路。
我们今天来实现的方法主要是根据借助函数的递归调用时的栈帧结构来实现的，用地址空间中的栈结合起来来实现回溯法的。
首先我们先来用图来理解一下

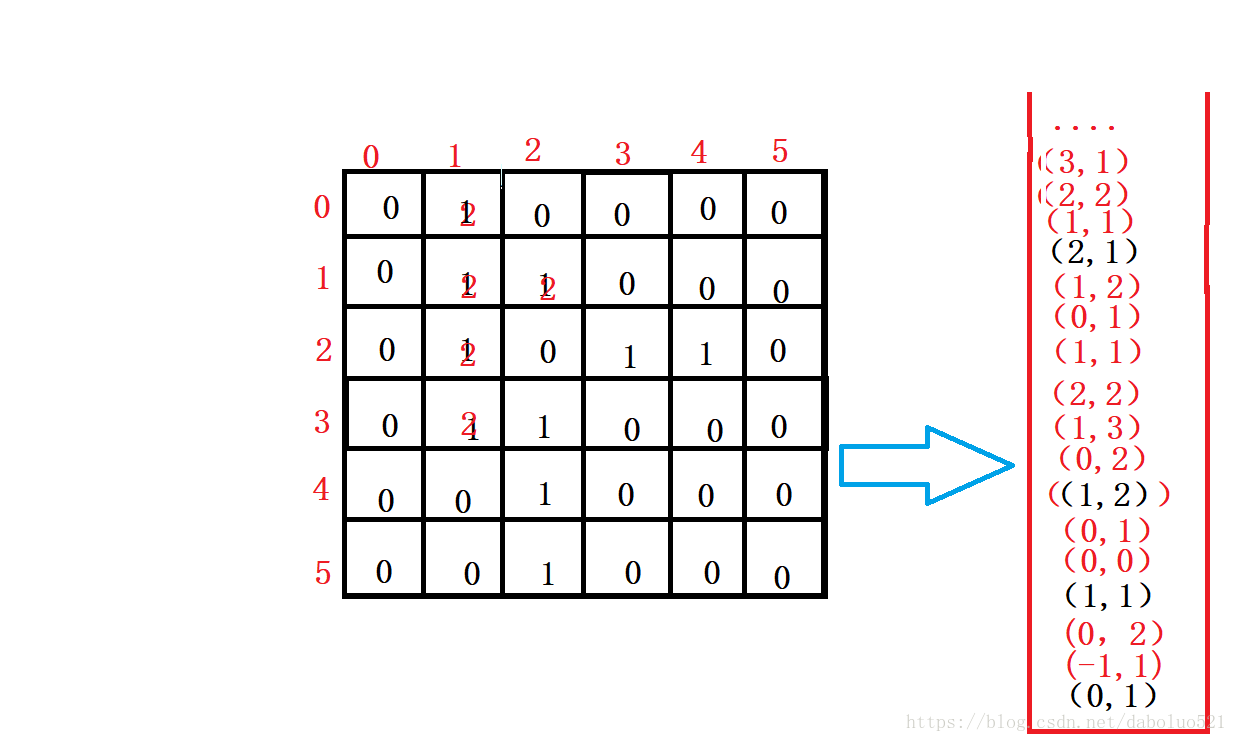
通过我们结合画图大致将出栈、入栈的结果画出来了，红色的坐标的含义就是我们被标记了的坐标，或者我们不能走过的路径。不符合的点就出栈。
代码实现：

#pragma once
#include <stdio.h>

#define ROW 6
#define COL 6

typedef struct Maze{
    int  map[ROW][COL];
}Maze;
typedef struct Point{
    int row;
    int col;
}Point;

void MazeInit(Maze* maze){
    int map[ROW][COL]={
    {0,1,0,0,0,0,},
    {0,1,1,0,0,0,},
    {0,1,0,1,1,0,},
    {0,1,1,0,0,0,},
    {0,0,1,0,0,0,},
    {0,0,1,0,0,0,},
    };
    int i=0;
    for(;i<ROW;i++){
    int  j=0;
    for(;j<COL;j++){
        maze->map[i][j]=map[i][j];
    }
    }
}
void MazePrint(Maze* maze){
    if(maze==NULL){
    return;
    }
    size_t i=0;
    for(;i<ROW;i++){
    size_t j=0;
    for(;j<COL;j++){
        printf("%2d",maze->map[i][j]);//2d表示的是我们打印的数前面空着，右对齐
        }
    printf("\n");
    }
    printf("\n");
}

int CanStay(Maze* maze,Point cur){
    //1、点在地图上
    //2、点对应的值为1
    if(maze==NULL){
    return 0;
    }
    if(cur.row<0 || cur.row>=ROW || cur.col<0 ||cur.col>=COL){
    return 0;
    }
    if(maze->map[cur.row][cur.col]==1){
    return 1;
    }
    return 0;
}
void Mark(Maze* maze,Point cur){
    if(maze==NULL){
    return;
    }
    maze->map[cur.row][cur.col]=2;
}
int  IsExit(Maze* maze,Point cur,Point entry){
    if(maze==NULL){
    return;
    }
  //  1、点在地图边缘上
  //  2、不是入口
  if(cur.row==0 || cur.col==0 || cur.row==ROW-1||cur.col==COL-1){
      if(cur.row==entry.row && cur.col==entry.col){
      //入口点返回0
     return 0;
      }
      return 1;

  }
  return 0;
}



void _HasPath(Maze *maze,Point cur,Point entry){
   printf("cur:%d,%d\n",cur.row,cur.col);
   if(maze==NULL){
    return;
    }
    //1、判断当前点是否能落脚（点在地图上，位置为1）
    if(!CanStay(maze,cur)){
    return;
    }
    //2、标记当前点是走过的点
    Mark(maze,cur);
    //3、判断当前点是否时出口（落在边缘上，并且不是入口）
    if(IsExit(maze,cur,entry)){
    printf("找到了路径\n");
    return;
    }
    //4、按照顺时针的顺序探测周围邻接的
    ////点（递归的调用HasPath）通过函数调用栈维护走过的路当函数返回时，就返回上一个位置
     Point up=cur;
     up.row-=1;
     _HasPath(maze,up,entry);

     Point right=cur;
     right.col+=1;
     _HasPath(maze,right,entry);

     Point down=cur;
     down.row+=1;
     _HasPath(maze,down,entry);

     Point left=cur;
     left.col-=1;
     _HasPath(maze,left,entry);

    //5、如果四个方向都探测过了，就直接进行返回
        return;
}
//使用递归的方法来查找迷宫上是否存在一条路经
void HasPath(Maze* maze,Point entry){
    if(maze==NULL){
    return;
    }
    _HasPath(maze,entry,entry);
}

代码执行过程如下：

 0 1 0 0 0 0
 0 1 1 0 0 0
 0 1 0 1 1 0
 0 1 1 0 0 0
 0 0 1 0 0 0
 0 0 1 0 0 0

cur:0,1
cur:-1,1
cur:0,2
cur:1,1
cur:0,1
cur:1,2
cur:0,2
cur:1,3
cur:2,2
cur:1,1
cur:2,1
cur:1,1
cur:2,2
cur:3,1
cur:2,1
cur:3,2
cur:2,2
cur:3,3
cur:4,2
cur:3,2
cur:4,3
cur:5,2
找到了路径
cur:4,1
cur:3,1
cur:4,1
cur:3,0
cur:2,0
cur:1,0
cur:0,0
 0 2 0 0 0 0
 0 2 2 0 0 0
 0 2 0 1 1 0
 0 2 2 0 0 0
 0 0 2 0 0 0
 0 0 2 0 0 0