K近邻法（KNN）

最新推荐文章于 2024-11-25 18:12:22 发布

原创最新推荐文章于 2024-11-25 18:12:22 发布 · 566 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#KNN

PR、ML、DL 专栏收录该内容

18 篇文章

订阅专栏

1、KNN算法简介

KNN（K-Nearest Neighbor）算法即K最邻近算法，是实现分类器中比较简单易懂的一种分类算法。K临近之所以简单是因为它比较符合人们直观感受，即人们在观察事物，对事物进行分类的时候，人们最容易想到的就是谁离那一类最近谁就属于哪一类，即俗话常说的“近朱者赤，近墨者黑”，人们自然而然地把这种观察方式延伸到数据分类处理领域。K-NN算法就是基于欧几里得距离推断事物类别的一种实现方法。

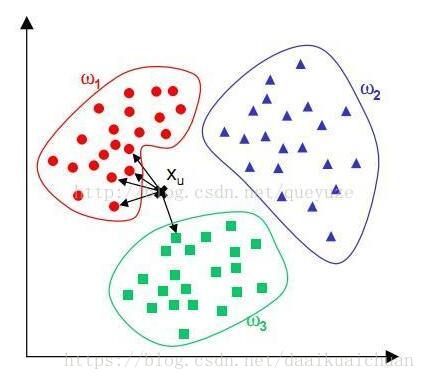
这里写图片描述

2、距离度量

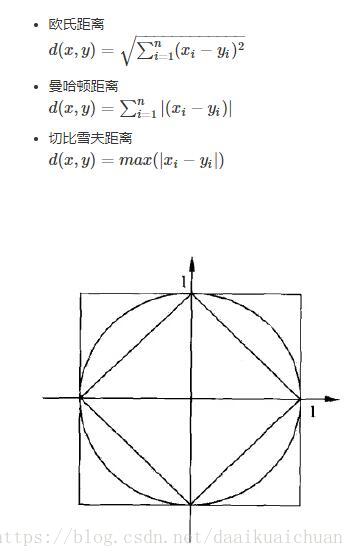
这里写图片描述

由图可知，p=1时与原点的Lp距离为1的点的图形是菱形，p=2是圆形。

3、KNN算法的思想

KNN算法假设给定的训练集中的实例都已经分好类了，对于新的实例，根据离它最近的k个训练实例的类别来预测它的类别。即这k个实例大多数属于某个类别则该实例就属于某个类别。比如k为5，离新实例a最近的5个样本的情况为，3个样本属于A类，1个样本属于B类，一个样本属于C类，那么新实例a属于A类。由此也说明了KNN算法的结果很大程度取决于K的选择。

这里写图片描述

4、KNN算法流程

（1）线性扫描

1. 计算测试数据与各个训练数据之间的距离；

2. 按照距离的递增关系进行排序；

3. 选取距离最小的K个点；

4. 确定前K个点所在类别的出现频率；

5. 返回前K个点中出现频率最高的类别作为测试数据的预测分类。

代码实现：

#include <iostream>
#include <vector>
#include <Eigen/Dense>
#include <cmath>
#include <algorithm>
#include <map>
#include <utility>

using namespace Eigen;
using namespace std;

const int n = 5;
const int N = 2;
const int k = 3;

int main()
{
    MatrixXd a(n, N + 1);
    a << 1, 2, 1,
        1.2, 0.1, 1,
        0.1, 1.4, 2,
        0.3, 3.5, 2,
        0.4, 2.0, 2;
    vector<pair<double, int>> dis;
    pair<double, int> pr;
    vector<double> test = { 0.5, 2.3 };
    for (int i = 0; i < n; ++i)
    {
        double d = 0.0;
        for (int j = 0; j < N; ++j)
        {
            d += pow((a(i, j) - test[j]), 2);
        }
        pr.first = sqrt(d);
        pr.second = a(i, 2);
        dis.push_back(pr);
    }
    cout << "计算测试数据与各个训练数据之间的距离：" << endl;
    for (auto d : dis)
        cout << d.first << " " << d.second << endl;
    cout << "按照距离的递增关系进行排序，选取距离最小的K个点：" << endl;
    partial_sort(dis.begin(), dis.begin() + k, dis.end());
    for (auto d : dis)
        cout << d.first << " " << d.second << endl;
    cout << "确定前K个点所在类别的出现频率：" << endl;
    map<double, int> mp;
    for (int i = 0; i < k; ++i)
        mp[dis[i].second]++;
    for (auto m : mp)
        cout << m.first << " " << m.second << endl;
    cout << "返回前K个点中出现频率最高的类别作为测试数据的预测分类：" << endl;
    vector<pair<int, int>> mp_test;
    for (auto it = mp.begin(); it != mp.end(); it++)
        mp_test.push_back(make_pair(it->first, it->second));
    sort(mp_test.begin(), mp_test.end(), [](pair<double, int> x, pair<double, int> y) -> bool {
        return x.second > y.second;
    });
    auto it = mp_test.begin();
    cout << it->first << endl;
    system("pause");
}

（2）kd树

线性扫描非常耗时，为了减少计算距离的次数提高效率，使用kd树方法，它能快速地找到查询点近邻。可以通过将搜索空间进行层次划分建立索引树以加快检索速度。对于二维空间，它最终要划分的空间类似如下，

这里写图片描述

决定在哪个维度上进行分割是由所有数据在各个维度的方差决定的，方差越大说明该维度上的数据波动越大，更应该再该维度上对点进行划分。例如x维度方差较大，所以以x维度方向划分。分割时一般取分割维度上的所有值的中值的点，比如下图，第一次计算方差较大的维度为x维度，中值点为A，以x=Ax分割，接着对分割后的点分别又继续分割，计算方差并寻找中值，以y=Cy、y=By分割，以此类推。

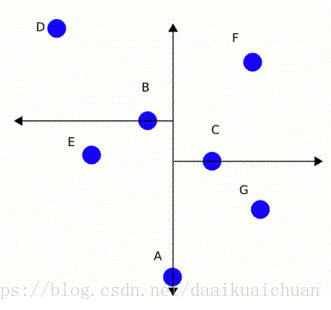
这里写图片描述

从根节点开始查找，直到叶子节点，整个过程将最短距离d和相应的点记录下来。回溯，通过计算待预测的点到分割平面的距离l与最短距离d比较，看是否要进入节点的相邻空间去查找。回溯的过程是为了确认是否有必要进入相邻子空间去搜索，当待预测点到最近点的距离d大于待预测点到分割面的距离l时，则需要到相邻子空间查找，否则则没必要，直接往上一层回溯。

5、KNN算法总结

（1）优点

1. 简单，易于理解，易于实现，无需估计参数，无需训练；

2. 适合对稀有事件进行分类（例如当流失率很低时，比如低于0.5%，构造流失预测模型）；

3. 特别适合于多分类问题(multi-modal,对象具有多个类别标签)，例如根据基因特征来判断其功能分类，kNN比SVM的表现要好。

（2）缺点

1. 懒惰算法，对测试样本分类时的计算量大，内存开销大，评分慢；

2. 可解释性较差，无法给出决策树那样的规则。

（3）常见问题

1. k值设定为多大？

k太小，分类结果易受噪声点影响；k太大，近邻中又可能包含太多的其它类别的点。（对距离加权，可以降低k值设定的影响）。k值通常是采用交叉检验来确定（以k=1为基准）。经验规则：k一般低于训练样本数的平方根。

2. 类别如何判定最合适？