聚合物心脏瓣膜材料选择新方法

聚合物假体心脏瓣膜设计的材料选择与性能指数

1 背景

由于瓣膜性心脏病需要更换心脏瓣膜的患者数量预计将从2003年的29万例增加到2050年的85万例。目前，这些患者的治疗主要依赖于外科植入的机械瓣膜或生物假体瓣膜。

然而，这些解决方案均不理想，它们只是将天然瓣膜疾病替换为“假体瓣膜疾病”——机械瓣膜需要终身抗凝，而生物假体的耐久性有限，约为15年。因此，自20世纪50年代以来，研究人员一直在寻求能够克服这些缺点的解决方案。

柔性瓣叶聚合物假体心脏瓣膜（PHV）已被提出作为一种潜在解决方案——有望在无需抗凝的情况下提供良好的长期耐久性和功能，但迄今为止尚无一种瓣膜在临床上取得成功，在过去40年的研发中，尚无任何瓣膜进入临床试验[1]。

因此，我们设计聚合物瓣膜的流程应被认真考虑。

聚合物瓣膜的设计可分为结构性瓣膜设计和材料选择问题。阿什比等人[2]，系统地提出了利用材料选择指数辅助工程部件定量设计的方法，本报告中，我们提出一种新的材料性能指数（PI）用于评估经导管心脏瓣膜（PHV）的潜在聚合物材料。我们将瓣叶确定为瓣膜的关键部件，因此本报告的重点是针对瓣叶的材料选择。

我们将材料“领域”的搜索范围限定在机械性能与生物组织相似的弹性体材料上。这使我们能够产生准生理流动。接下来，我们根据血液相容性（最小程度的炎症和血栓形成性）和生物稳定性（抗氧化和抗水解能力）筛选出一份候选材料清单。

多种弹性体和涂层满足这些标准。在经导管心脏瓣膜领域，已提出多种“生物相容性”和“生物稳定性”聚合物：多面体低聚倍半硅氧烷聚碳酸酯氨酯、聚苯乙烯（PS）‐嵌段‐聚异丁烯‐b‐PS（及交联型）、Elasteon、纤维素、PS‐b‐聚乙烯‐丙烯‐b‐PS 和聚乙烯‐透明质酸。在这一类材料中，我们旨在确定最适合用于经导管心脏瓣膜的聚合物。

耐久性和钙化是所有在体外或体内测试的柔性瓣叶聚合物瓣膜所面临的两种失效途径。耐久性取决于材料和瓣膜设计。尽管不同的瓣叶形态和尺寸可降低瓣叶应力，但决定应力的首要因素

瓣叶在舒张期受载时产生的应力是瓣叶厚度的函数；较厚的瓣叶应力较低。同时，我们必须关注瓣膜的血流动力学性能。通常，减小瓣叶厚度可降低平均压差[3]。

鉴于瓣叶厚度存在这些相互矛盾的标准，我们必须寻求一种折中方案，从而采用材料性能指标PI[2]。我们必须利用瓣叶厚度和适当的材料参数，建立血流动力学和耐久性之间的关系。

对于三叶瓣膜要成功发挥功能，每个瓣叶的曲率必须发生反转，理论上，TPGmax/Et³，其中TPGmax为最大跨瓣压差，E为杨氏模量（或弯曲模量），t为瓣叶厚度。

霍沃思[4]利用撕裂强度作为预测寿命的参数，基于该关系进行流体动力学分析。然而，使用撕裂强度在部分情况下失败了，因为它描述的是应力状态远高于生理条件下的失效情况。帕尔费耶夫等人[5]对此进行了改进，通过比较聚合物在22赫兹下经过10⁷循环次数后的磨损极限来进行评估。我们对候选聚合物进行了频率扫描动态机械分析，结果表明它们在15–20赫兹时发生转变，因此在此类高频率下进行测试无法准确预测低频行为。

自20世纪80年代以来，其他领域对橡胶部件失效的疲劳测试与预测开展了大量研究。特别是，在各种橡胶部件的循环应变中，利用裂纹扩展模型预测长期行为已成功应用[6]。

我们现在提出一种基于循环疲劳理论的新型材料性能指标，用于改进聚合物心脏瓣膜的设计。

2 方法

我们采用两种不饱和嵌段共聚物（BCPs）和三种饱和BCPs进行实验筛选：苯乙烯‐聚异戊二烯‐苯乙烯三嵌段共聚物，含18 wt% 苯乙烯（SIS18）和30%苯乙烯（SIS30）；以及三种饱和BCPs：苯乙烯‐聚乙烯‐聚丙烯‐苯乙烯三嵌段共聚物，含22%苯乙烯（SEPS22）；苯乙烯‐聚乙烯‐聚丁烯‐苯乙烯三嵌段共聚物，含20%苯乙烯（SEBS20）（均为Kraton公司产品）；苯乙烯‐聚异丁烯‐苯乙烯三嵌段共聚物，含30%苯乙烯（Inno‐via）。这些BCPs在纳米尺度发生相分离，形成在软嵌段连续相中分布的刚性PS圆柱结构。同时将上述材料与先前用于心血管应用的Pellethane 2363‐80AE进行对比。这些聚合物通过压缩成型制备成厚度为0.5毫米的样品，成型温度为 160 °C。所得聚合物具有力学各向异性，可沿刚性聚合物相取向方向平行（L）或垂直（R）拉伸。样品在单轴和平面拉伸模式下进行力学表征。所有测试均使用Stable Microsystems质地分析仪完成。

寿命预测方法由马尔斯和法特米[6]进行了详细描述。应变能释放率是描述材料吸收能量（可用于生成新表面）的最合适方式，并用于裂纹扩展预测。

简而言之，在平面拉伸试样中使用剃刀刀片切割出25毫米裂纹，随后在不同的最大应变下进行循环拉伸，并通过相机监测裂纹长度。对图像进行分析，测量得到稳定裂纹扩展速率。确定裂纹扩展速率与应变能释放率之间的幂律关系。

$$
\frac{dc}{dN} = B T^F
$$

其中c为裂纹长度，N为循环次数，T为能量释放率，在平面拉伸情况下，$ T = W h $，其中W为应变能密度，h为未拉伸试样长度，B和F为通过拟合确定的常数。该表达式可积分以估算材料中固有缺陷引起的裂纹成核寿命

$$
W_{\text{max}} = \left[ \frac{1}{F - 1} \cdot \frac{1}{B N_f} \left( \frac{1}{c_0^{F-1}} - \frac{1}{c_f^{F-1}} \right) \right]^{\frac{1}{F}} \cdot \frac{1}{2k}
$$

其中，$ N_f $为失效前的循环次数，$ c_0 $和$ c_f $分别为初始裂纹尺寸和失效时的裂纹尺寸，k为通过实验确定的与缺陷拉伸后长宽比相关的几何依赖因子。

通过薄的无裂纹拉伸试样进行循环应变实验来验证该模型，其中裂纹扩展会迅速导致试样失效。

阀门的开启需要瓣叶发生弯曲。因此，最相关的材料性能是弯曲模量。我们通过三点弯曲装置测量了该性能。

3 结果

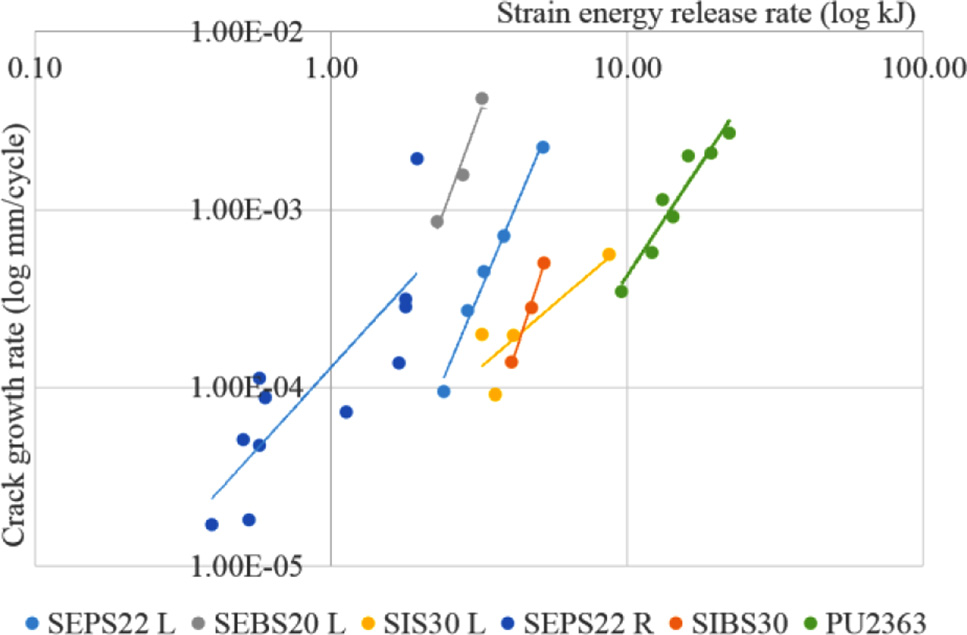
取向嵌段共聚物和各向同性聚氨酯材料的宏观裂纹扩展与应变能释放率的关系

表1 使用性能指数 $ E / W_{\text{max}}^3 $ 对材料进行排序，SIBS30-L是在心脏瓣膜中应用潜力最大的材料，SEPS22-R是最小

材料	方向	$ E_{\text{flex}} $ (MPa)	$ B $ (m⁻¹)	$ F $	$ W_{\text{max}} $ (MJ/m³)	PI = $ E_{\text{flex}} / W_{\text{max}}^3 $
SIS18	L	1.7	1.2×10⁻⁵	3.2	0.48	154
SIS30	L	3.1	2.1×10⁻⁵	3.0	0.52	220
SEBS20	R	2.5	1.8×10⁻⁵	3.1	0.50	200
SEPS22	R	2.0	1.5×10⁻⁵	3.3	0.55	119
SEPS22	L	3.8	2.5×10⁻⁵	2.9	0.45	420
Inno-via	—	2.8	2.0×10⁻⁵	3.1	0.51	213
Pellethane 2363-80AE	—	12.0	3.0×10⁻⁵	2.8	0.40	1875

图1显示了平面样品中每种材料的尖锐裂纹（具有自然尖端）在能量释放率作用下的裂纹扩展速率。对每个关系拟合了巴黎幂律模型，其参数列于表1中。随后计算了最大允许应变能密度 $ W_{\text{max}} $，以避免失效，其中循环次数 $ N_f = 10^9 $，裂纹长度 $ c_0 = 0.02 \,\text{mm} $，临界裂纹长度 $ c_f = 0.3 \,\text{mm} $（天然小叶厚度），以及 $ k = 2 $。

给定 $ W_{\text{max}} $ 和 $ E_{\text{flex}} $，每种材料的性能指标 PI 计算如下：

$$
\text{PI} = \frac{E_{\text{flex}}}{W_{\text{max}}^3}
$$

性能指标PI在应变能密度W与E的对数‐对数图中表现为斜率为1/3的直线。$ E_{\text{flex}} $ 与 $ W_{\text{max}} $ 的关系如表1所示。

参考聚氨酯材料比其他材料明显更硬，但疲劳强度并未显著更高，因此其性能指标相对较差。取向嵌段共聚物在受力方向为其软方向（垂直于圆柱体）时更具柔韧性，而在圆柱体方向上具有相对较高的疲劳应力极限，从而改善了其性能指标。

4 解释

通过最小化由 $ E $ 和 $ W_{\text{max}} $ 构建的PI，可从给定的候选材料中选择最优材料。尽管某些材料可能表现出良好的使用寿命特性，例如图1中的SIS30，但其刚度要求瓣叶较薄，因此不太适合用于经导管心脏瓣膜的瓣叶。

随后可以估算出瓣叶的最佳厚度。根据Bernacca等人[3]，对瓣叶模量和厚度变化所进行的研究，我们确定了 $ E t^3 $ 的最大值（注：此处为杨氏模量）。在他们的实验中，该值出现在 $ 1.8 \times 0.2 \times 10^4 \, \text{Nm} $。基于此信息，可根据材料的机械性能估算出最大瓣叶厚度。

性能指标（PI）还使我们能够定量地展示使用力学各向异性材料所带来的优势。一种各向异性材料（SEPS22）在垂直方向和平行方向均进行了测试。PI的显著提升表明，如果这些刚性圆柱体能够在瓣膜的瓣叶中实现定向排列，则可以在不损害血流动力学的前提下，增加瓣叶厚度，从而提高耐久性。

我们报道了一种基于机械性能选择聚合物心脏瓣膜材料的新方法，然而我们也承认，生物相容性和生物稳定性在材料选择中也起着至关重要的作用。在此情况下，取向良好且饱和的嵌段共聚物相较于参考的聚氨酯材料具有更优的性能指标。目前，一种苯乙烯类嵌段共聚物材料已被选用于聚合物心脏瓣膜中。