链式二叉树

原创已于 2025-06-27 11:50:59 修改 · 460 阅读

4 ·

CC 4.0 BY-SA版权

文章标签：

#数据结构 #算法 #c语言 #二叉树 #队列

于 2025-06-21 16:02:50 首次发布

初阶数据结构与算法专栏收录该内容

9 篇文章

订阅专栏

Tree.h文件

#pragma once
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<stdbool.h>

//定义链式结构的二叉树
typedef char BTDataType;
typedef struct BinaryTreeNode
{
	BTDataType data;
	struct BinaryTreeNode* left;
	struct BinaryTreeNode* right;
}BTNode;

//前序遍历——根左右
void preOrder(BTNode* root);

//中序遍历——左中右
void inOrder(BTNode* root);

//后序遍历——左右中
void postOrder(BTNode* root);

//二叉树结点个数
int BinaryTreeSize(BTNode* root);

//二叉树叶子结点个数
int BinaryTreeLeafSize(BTNode* root);

//二叉树第K层结点个数
int BinaryTreeLevelKSize(BTNode* root, int k);

//二叉树的深度/高度
int BinaryTreeDepth(BTNode* root);

//二叉树查找值为x的结点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x);

//二叉树的销毁
void BinaryTreeDestroy(BTNode** root);


//层序遍历
void leverOrder(BTNode* root);

//判断二叉树是否为完全二叉树
bool BinaryTreeComplete(BTNode* root);

Tree.c文件

#include"Tree.h"
#include"Queue.h"

//前序遍历——根左右
void preOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	printf("%c ", root->data);
	preOrder(root->left);
	preOrder(root->right);
}

//中序遍历——左根右
void inOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	inOrder(root->left);
	printf("%c ", root->data);
	inOrder(root->right);
}

//后序遍历——左右根
void postOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	postOrder(root->left);
	postOrder(root->right);
	printf("%c ", root->data);
}

//二叉树结点个数
int BinaryTreeSize(BTNode* root)
{
	if (root == NULL)
	{
		return 0;
	}
	return 1 + BinaryTreeSize(root->left)
		+ BinaryTreeSize(root->right);
}

//二叉树叶子结点个数
int BinaryTreeLeafSize(BTNode* root)
{
	if (root == NULL)
	{
		return 0;
	}
	if (root->left == NULL && root->right == NULL)
	{
		return 1;
	}
	return BinaryTreeLeafSize(root->left) 
		+ BinaryTreeLeafSize(root->right);
}


//二叉树第K层结点个数
int BinaryTreeLevelKSize(BTNode* root, int k)
{
	if (root == NULL)
	{
		return 0;
	}
	if (k == 1)
	{
		return 1;
	}
	return BinaryTreeLevelKSize(root->left, k - 1)
		+ BinaryTreeLevelKSize(root->right, k - 1);
}

//二叉树的深度/高度
int BinaryTreeDepth(BTNode* root)
{
	if (root == NULL)
	{
		return 0;
	}
	int leftDepth = BinaryTreeDepth(root->left);
	int rightDepth = BinaryTreeDepth(root->right);

	return 1 + (leftDepth > rightDepth ? leftDepth : rightDepth);
}

//二叉树查找值为x的结点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{
	//采取前序遍历
	if (root == NULL)
	{
		return NULL;
	}
	if (root->data == x)
	{
		return root;
	}
	BTNode* leftFind = BinaryTreeFind(root->left, x);
	if (leftFind)
	{
		//左子树找到了就无需遍历右子树了 直接返回
		return leftFind;
	}
	BTNode* rightFind = BinaryTreeFind(root->right, x);
	if (rightFind)
	{
		return rightFind;
	}
	return NULL;
}


//二叉树的销毁
void BinaryTreeDestroy(BTNode** root)
{
	//采取后序遍历
	if (*root == NULL)
	{
		return;
	}
	//由于left在前面结构体中创建的是一级指针
	//但销毁函数接收的是二级指针，因此传参要取地址
	//同时注意*的优先级小于->  因此*root加括号
	BinaryTreeDestroy(&((*root)->left));
	BinaryTreeDestroy(&((*root)->right));

	free(*root);
	*root = NULL;
}



//层序遍历（借助数据结构—队列）
void leverOrder(BTNode* root)
{
	Queue q;
	//初始化队列
	QueueInit(&q);
	//根结点入队
	QueuePush(&q, root);
	while (!QueueEmpty(&q))
	{
		//取队头  出队头
		BTNode* top = QueueFront(&q);
		QueuePop(&q);
		printf("%c ", top->data);

		//根结点的非空左右孩子入队列
		if (top->left)
			QueuePush(&q, top->left);
		if (top->right)
			QueuePush(&q, top->right);
	}

	//销毁队列
	QueueDestroy(&q);
}


//判断二叉树是否为完全二叉树（借助数据结构—队列）
bool BinaryTreeComplete(BTNode* root)
{
	Queue q;
	//初始化队列
	QueueInit(&q);
	//根结点入队
	QueuePush(&q, root);
	while (!QueueEmpty(&q))
	{
		//取队头  出队头
		BTNode* top = QueueFront(&q);
		QueuePop(&q);

		if (top == NULL)
		{
			break;
		}
		//如果根结点不为空，取其左右孩子放入队列
		QueuePush(&q, top->left);
		QueuePush(&q, top->right);
	}
	//跳出第一次循环，此时只是队头取到了NULL
	//但队列不一定为空，故第二次循环
	while (!QueueEmpty(&q))
	{
		//取队头  出队头
		BTNode* top = QueueFront(&q);
		QueuePop(&q);

		if (top != NULL)
		{
			QueueDestroy(&q);
			return false;
		}
	}
	//二次循环遍历结果均为NULL，则为完全二叉树
	//销毁队列
	QueueDestroy(&q);
	return true;
}

test.c文件

#include"Tree.h"

//创建新节点
BTNode* buyNode(char x)
{
	BTNode* newNode = (BTNode*)malloc(sizeof(BTNode));
	newNode->data = x;
	newNode->left = newNode->right = NULL;

	return newNode;
}

//构造链式二叉树
BTNode* CreateBinaryTree()
{
	BTNode* nodeA = buyNode('A');
	BTNode* nodeB = buyNode('B');
	BTNode* nodeC = buyNode('C');
	BTNode* nodeD = buyNode('D');
	BTNode* nodeE = buyNode('E');
	BTNode* nodeF = buyNode('F');

	nodeA->left = nodeB;
	nodeA->right = nodeC;
	nodeB->left = nodeD;
	nodeC->left = nodeE;
	nodeC->right = nodeF;

	//返回二叉树根结点
	return nodeA;
}

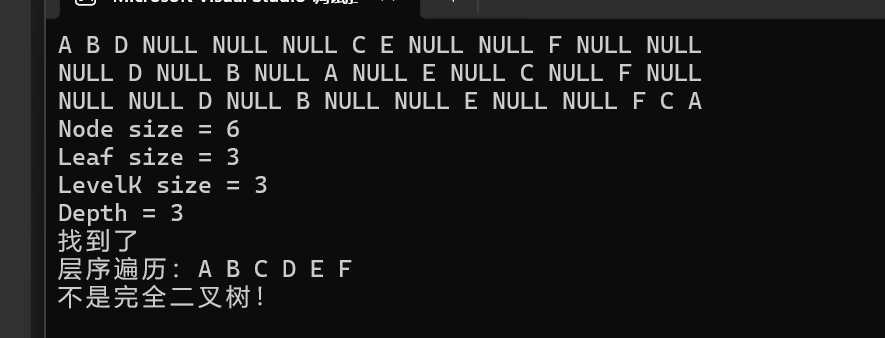
void test01()
{
	BTNode* root = CreateBinaryTree();
	preOrder(root);
	printf("\n");
	inOrder(root);
	printf("\n");
	postOrder(root);
	printf("\n");

	printf("Node size = %d\n", BinaryTreeSize(root));

	printf("Leaf size = %d\n", BinaryTreeLeafSize(root));

	printf("LevelK size = %d\n", BinaryTreeLevelKSize(root, 3));

	printf("Depth = %d\n", BinaryTreeDepth(root));

	if (BinaryTreeFind(root, 'E'))
	{
		printf("找到了\n");
	}
	else
	{
		printf("未找到\n");
	}

	printf("层序遍历：");
	leverOrder(root);

	bool ret = BinaryTreeComplete(root);
	if (ret)
	{
		printf("\n是完全二叉树！\n");
	}
	else {
		printf("\n不是完全二叉树！\n");
	}

	BinaryTreeDestroy(&root);
}

int main()
{
	CreateBinaryTree();
	test01();
	return 0;
}

测试运行结果如下

数据结构之队列功能的引用说明

实现二叉树最后的两个功能（1.层序遍历 2.判断二叉树是否为完全二叉树）需要借助数据结构队列来完成，需要注意的是，引用之前的队列实现的代码文件，记得更改队列结点数据类型QDataType为struct BinaryTreeNode*（原类型是int），并且需要记得在Tree.c文件中引用头文件"Queue.h"。从思路分别如下。

1.层序遍历

层序遍历不同于前中后序遍历，该遍历方法是从根结点自上而下、从左往右依次遍历。初始化队列后将根结点放入队列，只要队列不为空就开始循环，取队首结点并打印，然后结点出队，如果该根结点的左右孩子不为空，则将其孩子也放入队列中，重复以上操作，全部打印并出队后，完成遍历结束循环。

void leverOrder(BTNode* root)
{
	Queue q;
	//初始化队列
	QueueInit(&q);
	//根结点入队
	QueuePush(&q, root);
	while (!QueueEmpty(&q))
	{
		//取队头  出队头
		BTNode* top = QueueFront(&q);
		QueuePop(&q);
		printf("%c ", top->data);

		//根结点的非空左右孩子入队列
		if (top->left)
			QueuePush(&q, top->left);
		if (top->right)
			QueuePush(&q, top->right);
	}

	//销毁队列
	QueueDestroy(&q);
}

2.判断二叉树是否为完全二叉树

首先得了解完全二叉树的结构定义，一是除了最后一层之外，任意层的结点数量均达到最大；二是最后一层的结点从左往右顺序依次排列。依旧需要借助队列来实现，初始化队列后将根结点放入队列，只要队列不为空就开始循环，取队首结点，然后首结点出队，不同于层序遍历的是，无论根结点的左右孩子是否为空，都放入队列中。如果取队首结点取到了NULL，则结束循环，开始第二次循环，循环条件与第一次相同，如果二次循环取队首结点取到了非空结点，则可以判断不是完全二叉树，因为结点不是从左往右顺序分布的，如果取到NULL，则继续循环，直到队列为空都没有取到非空结点，则可以判断该二叉树是完全二叉树。

bool BinaryTreeComplete(BTNode* root)
{
	Queue q;
	//初始化队列
	QueueInit(&q);
	//根结点入队
	QueuePush(&q, root);
	while (!QueueEmpty(&q))
	{
		//取队头  出队头
		BTNode* top = QueueFront(&q);
		QueuePop(&q);

		if (top == NULL)
		{
			break;
		}
		//如果根结点不为空，取其左右孩子放入队列
		QueuePush(&q, top->left);
		QueuePush(&q, top->right);
	}
	//跳出第一次循环，此时只是队头取到了NULL
	//但队列不一定为空，故第二次循环
	while (!QueueEmpty(&q))
	{
		//取队头  出队头
		BTNode* top = QueueFront(&q);
		QueuePop(&q);

		if (top != NULL)
		{
			QueueDestroy(&q);
			return false;
		}
	}
	//二次循环遍历结果均为NULL，则为完全二叉树
	//销毁队列
	QueueDestroy(&q);
	return true;
}

附录：队列的功能代码实现

Queue.h文件

#pragma once
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<stdbool.h>

typedef struct BinaryTreeNode* QDataType;
//typedef struct BTNode* QDataType;

//队列结点的结构
typedef struct QueueNode
{
	QDataType data;
	struct QueueNode* next;
}QueueNode;

//队列的结构
typedef struct Queue
{
	QueueNode* phead;
	QueueNode* ptail;
}Queue;


//队列的初始化
void QueueInit(Queue* pq);

//入队——队尾
void QueuePush(Queue* pq, QDataType x);

//队列判空
bool QueueEmpty(Queue* pq);

//出队
void QueuePop(Queue* pq);

//取队头数据
QDataType QueueFront(Queue* pq);

//取队尾数据
QDataType QueueBack(Queue* pq);

//队列有效个数
int QueueSize(Queue* pq);

//销毁队列
void QueueDestroy(Queue* pq);

Queue.c文件

#include"Queue.h"

//队列初始化
void QueueInit(Queue* pq)
{
	assert(pq);
	pq->phead = pq->ptail = NULL;
}

//入队——队尾
void QueuePush(Queue* pq, QDataType x)
{
	assert(pq);
	//申请空间
	QueueNode* newnode = (QueueNode*)malloc(sizeof(QueueNode));
	if (newnode == NULL)
	{
		perror("malloc fail!");
		exit(1);
	}
	newnode->data = x;
	newnode->next = NULL;
	//队列为空
	if (pq->phead == NULL)
	{
		pq->phead = pq->ptail = newnode;
	}
	//非空
	else {
		pq->ptail->next = newnode;
		pq->ptail = pq->ptail->next;
	}
}

//队列判空
bool QueueEmpty(Queue* pq)
{
	assert(pq);
	return pq->phead == NULL;
}

//出队——队头
void QueuePop(Queue* pq)
{
	assert(!QueueEmpty(pq));
	//只有一个结点，phead和ptail都要置空，否则ptail变野指针
	if (pq->phead == pq->ptail)
	{
		free(pq->phead);
		pq->phead = pq->ptail = NULL;
	}
	else {
		QueueNode* next = pq->phead->next;
		free(pq->phead);
		pq->phead = next;
	}
}

//取队头数据
QDataType QueueFront(Queue* pq)
{
	assert(!QueueEmpty(pq));
	return pq->phead->data;
}

//取队尾数据
QDataType QueueBack(Queue* pq)
{
	assert(!QueueEmpty(pq));
	return pq->ptail->data;
}

//队列有效个数
int QueueSize(Queue* pq)
{
	QueueNode* pcur = pq->phead;
	int size = 0;
	while (pcur)
	{
		size++;
		pcur = pcur->next;
	}
	return size;
}

//销毁队列
void QueueDestroy(Queue* pq)
{
	assert(pq);
	QueueNode* pcur;
	pcur = pq->phead;
	while (pcur != NULL)
	{
		QueueNode* next = pcur->next;
		free(pcur);
		pcur = next;
	}
	pq->phead = pq->ptail = NULL;
}