《关于浅浅理解一下树这件事》

树与图

初次见面树可能会认为和无向图差不多，其实树就是不包含回路的连通无向图
因为树有着“不包含回路”的特点，故可以有以下几点

• 一颗树中的任意两个节点有且仅有唯一的一条路径连通。
• 一棵树如果有n个节点，那么它一定恰好有n-1条边。
• 在一棵树中加一条边将会构成一个回路。

树

为了讲解方便，这里浅对树进行一些定义。

1. 树是指任意两个节点间有且仅有一条路径的无向图。
   一种树可以有多种形态。
   
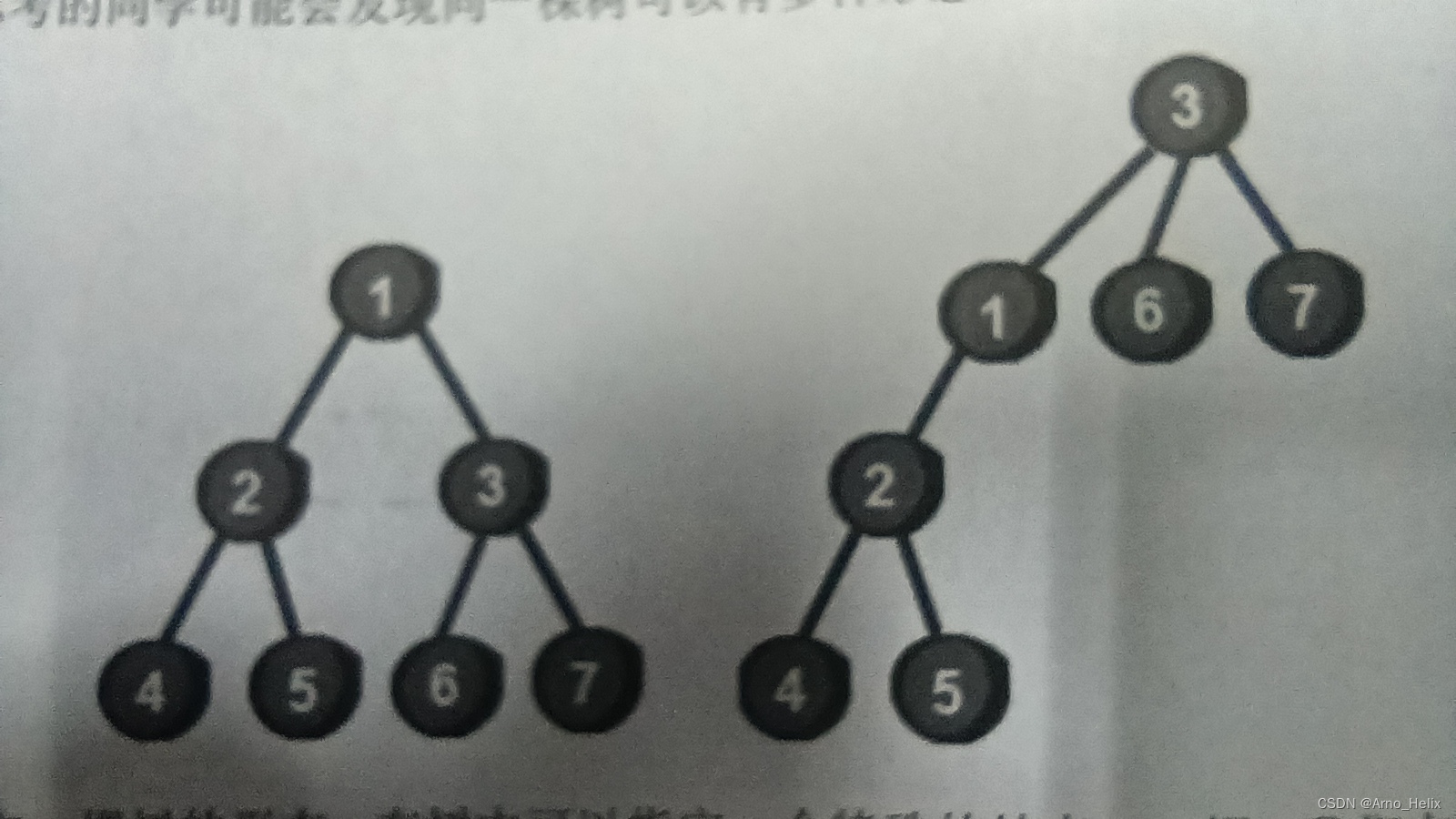
   为了确定一棵树的形态，在树中可以指定一个特殊的结点——根结点
   比如左边这棵树的根结点是1号结点，右边这棵树的结点是3号结点。
   一棵树有且仅有一个根结点
   除了根结点外每个结点都有父结点，有父结点就有子结点，当然最小的儿子就没有儿子了，没有儿子的结点我们称之为“叶结点”，来对应没有父亲的“根结点”
   看左边的树1号结点是根结点同时也是2，3号结点的父结点，2号结点又是4，5号结点的父结点，这关系显而易见。

二叉树

二叉树是一种特殊的树，二叉树的特点是每个结点最多有两个儿子，左边叫左儿子，右边叫右儿子
二叉树要么为空要么由左子树和右子树构成

• 二叉树的使用范围最广，一棵多叉树也可以转化为二叉树
  二叉树有两种特殊的二叉树，满二叉树，完全二叉树
  满二叉树：
  每个内部结点都有两个子结点（满二叉树的所有叶结点都有同样的深度）严格定义为：深度为h且有(2^h)-1个结点的二叉树
  完全二叉树：
  一棵二叉树除了最右边位置上有一个或者几个叶结点缺少外，其他是丰满的。严格定义为：若设二叉树的高度为h，除第h层外，其他各层1~h-1的结点数都达到最大数，第h层从右往左连续缺若干个结点。（一个结点如果有右结点，那么他必有左结点）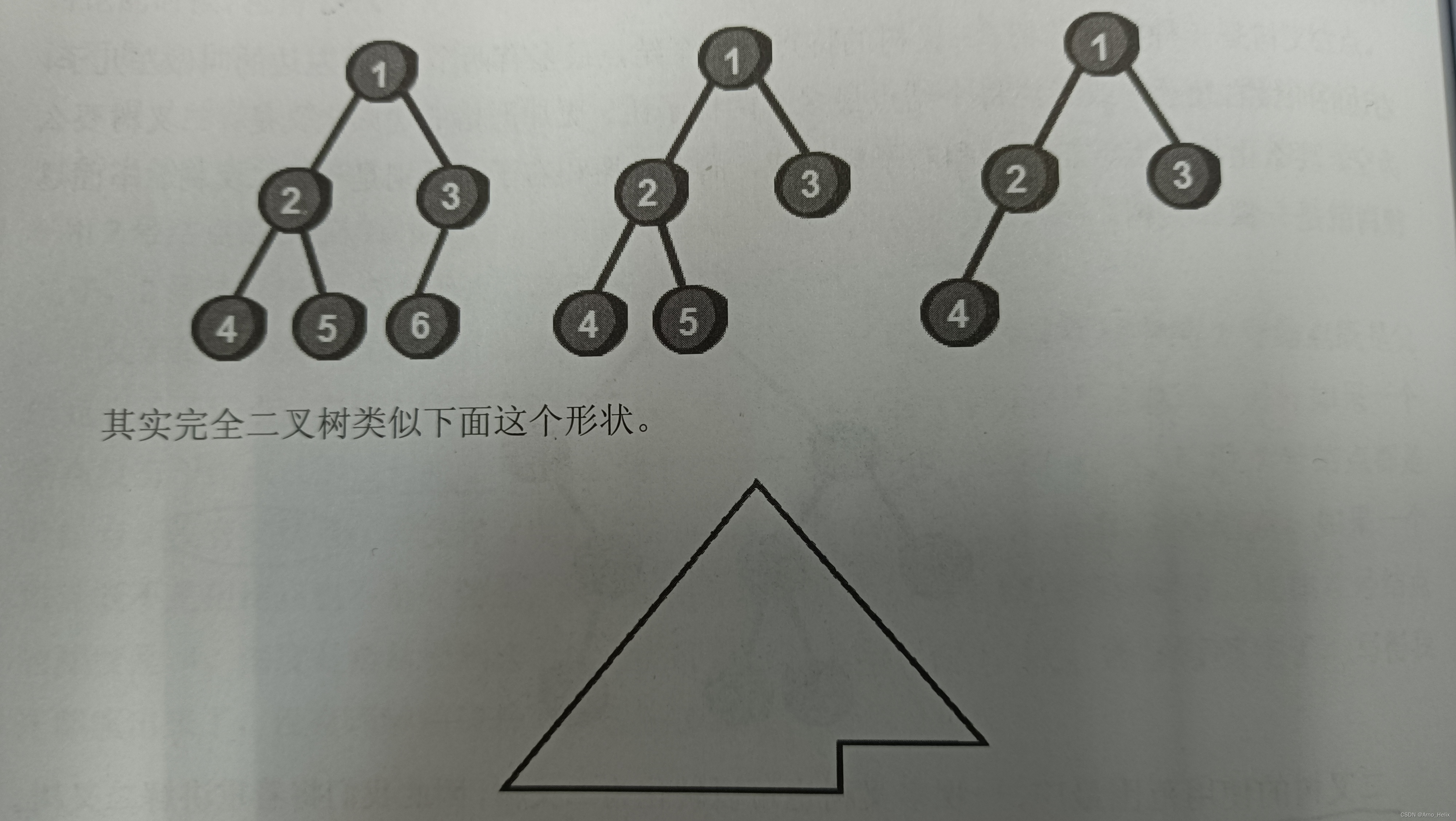

看看树的结构体

typedef struct BiTNode{
    TElemType data;//数据域
    struct BiTNode *lchild,*rchild;//左右孩子指针
    struct BiTNode *parent;//可以不要
}BiTNode;

采用链式存储二叉树时，其节点结构由 3 部分构成：
指向左孩子节点的指针（Lchild）；
节点存储的数据（data）；
指向右孩子节点的指针（Rchild）；
在后面加入父结点指针，我们可以很轻松地找到各节点的父节点，在解决实际问题时，用合适的链表结构存储二叉树，可以起到事半功倍的效果。
其实可以发现如果没有父结点的指针域的话，挺像链表的。
树里面其实有一种特殊的树：斜树

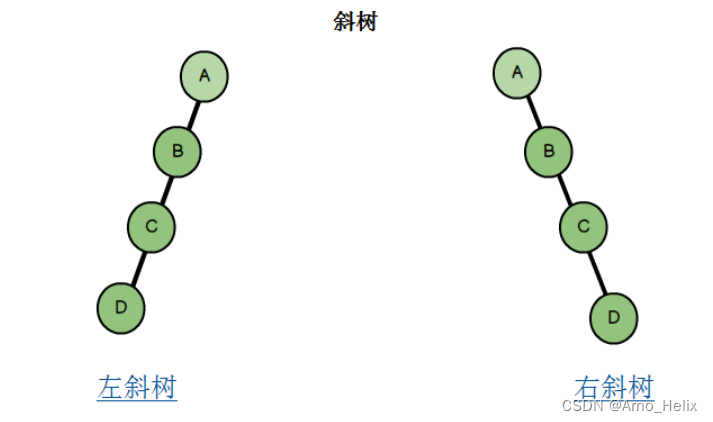
所有节点都只有左子树的二叉树叫做左斜树，所有节点都只有右子树的二叉树叫做右斜树。(本质就是链表)
看看就好。
在某些实际场景中，可能会做 “查找某节点的父节点” 的操作，这时可以在节点结构中再添加一个指针域，用于各个节点指向其父亲节点

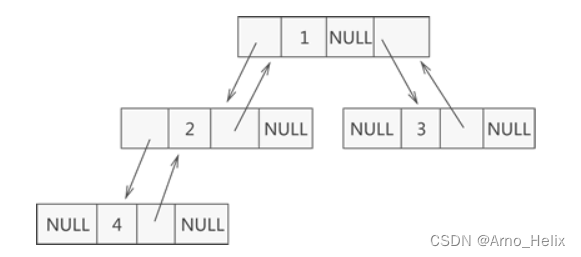
二叉树的实现方法一般有两种，分别为：

• 链式存储结构
• 数组

1. 先看看链式存储结构的双亲表示法
   这是表示方法

#include<stdio.h>
#include<stdlib.h>
#define MAX_SIZE 20
typedef char ElemType;//宏定义树结构中数据类型
typedef struct Snode  //结点结构
{
    ElemType data;
    int parent;
}PNode;

typedef struct  //树结构 
{
    PNode tnode[MAX_SIZE];
    int n;                 //结点个数
}PTree;

PTree InitPNode(PTree tree) {
    int i, j;
    char ch;
    printf("请输出节点个数:\n");
    scanf("%d", &(tree.n));

    printf("请输入结点的值其双亲位于数组中的位置下标:\n");
    for (i = 0; i < tree.n; i++) {
        getchar();
        scanf("%c %d", &ch, &j);
        tree.tnode[i].data = ch;
        tree.tnode[i].parent = j;
    }
    return tree;
}

void FindParent(PTree tree) {
    char a;
    int isfind = 0;
    printf("请输入要查询的结点值:\n");
    getchar();
    scanf("%c", &a);
    for (int i = 0; i < tree.n; i++) {
        if (tree.tnode[i].data == a) {
            isfind = 1;
            int ad = tree.tnode[i].parent;
            printf("%c的父节点为 %c,存储位置下标为 %d", a, tree.tnode[ad].data, ad);
            break;
        }
    }
    if (isfind == 0) {
        printf("树中无此节点");
    }
}

int main() {
    PTree tree;
    for (int i = 0; i < MAX_SIZE; i++) {
        tree.tnode[i].data = " ";
        tree.tnode[i].parent = 0;
    }
   
    tree = InitPNode(tree);
    FindParent(tree);
    return 0;
}

还有一种就是通过数组下标来表示树了，我们在之前的学习排序的时候，有一种排序方法叫做堆排序，他所采用的方法就是通过数组及其下标来表示树，然后利用树的特征来进行排序，这个有机会的话可以细讲一下。