数据统计分析解决方案_统计和解决方案

翻译 于 2020-06-29 15:43:58 发布 · 2.7k 阅读 · 0 ·
CC 4.0 BY-SA版权
原文链接：https://www.ibm.com/developerworks/java/library/j-benchmark2/index.html
文章标签：

#大数据 #编程语言 #python #机器学习 #人工智能

本文深入探讨了Java代码基准测试的复杂性，强调了统计在评估性能中的关键作用，介绍了用于进行基准测试的软件框架，并通过实例展示了如何解决常见的性能问题。

摘要生成于 C知道 ，由 DeepSeek-R1 满血版支持， 前往体验 >

这个由两部分组成的文章的第1部分将指导您解决与基准Java代码相关的许多陷阱。 第二部分涵盖两个不同的领域。 首先，它描述了一些基本统计数据，这些数据可用于应对基准测试中不可避免的测量变化。 其次，它介绍了用于进行基准测试的软件框架，并在一系列工作示例中使用它来说明要点。

统计

如果只需要执行一个执行时度量，并且可以使用一个度量来比较不同代码的性能，那将很方便。 令人遗憾的是，这种方法的普及并不能胜过其无效性-太多的变化来源无法让您信任一次测量。 在第1部分中 ，我提到了时钟分辨率，复杂的JVM行为和自动资源回收作为噪声源。 这些只是一些可能随机或系统地偏向基准的因素。 可以采取措施来减轻其中的一些负担。 如果您对它们足够了解，那么您甚至可以执行反卷积 （请参阅参考资料 ）。 但是这些补救措施从来都不是完美的，因此最终您必须应对这些变化。 唯一的方法就是进行大量测量并使用统计数据得出可靠的结论。 忽略此部分的后果自负，因为“拒绝进行算术的人注定要胡说八道”（请参阅参考资料 ）。

补充材料

本文的配套站点包括完整的示例代码包和一个详细探讨统计问题的补充。 请参阅相关信息的链接，同伴网站。

我将提供足够的统计数据来解决这些常见的性能问题：

  • 任务A比任务B执行得快吗？
  • 这个结论是可靠的，还是测量fl幸？

如果进行多次执行时测量，则可能要计算的第一个统计信息是一个总结其典型值的数字 （请参阅参考资料 ，获取Wikipedia本文中有关统计概念的定义的链接）。 最常见的度量是算术平均值 ，通常称为平均值或平均值 。 它是所有度量的总和除以度量的数量：

平均值x =求和i = 1，n （x i ）/ n

在随附的网站上可以找到本文的补充（请参阅参考资料 ），其中包括除均值之外的其他度量的讨论。 参见平均值部分的替代方法 。

使用几次测量的平均值来量化性能肯定比使用一次测量的精度更高，但是对于确定哪个任务执行得更快，可能不够。 例如，假设任务A的执行时间的平均值为1毫秒，任务B的平均值为1.1毫秒。 您是否应该自动得出结论，任务A比任务B快？ 如果您还知道任务A的测量值范围是0.9到1.5毫秒，而任务B的测量值范围是1.09到1.11毫秒，则可能不知道。 因此，您还需要解决测量范围 。

描述测量范围（或散布）的最常用统计量是标准偏差 ：

sd x = sqrt {和i = 1，n （[x i-平均值x ] 2 ）/ n}

标准偏差如何量化测量散点？ 好吧，这取决于您对测量的概率密度函数 （PDF）的了解。 您做出的假设越强，得出的结论就越好。 本文补编的``将标准偏差与测量散点相关''部分对此进行了更详细的探讨，并得出结论，在基准测试环境中，合理的经验法则是至少95％的测量值应在平均值的三个标准偏差之内 。

那么，如何使用平均值和标准偏差来确定两个任务中哪个更快？ 引用上述经验法则，最简单的情况是两个任务的均值之间相隔三个以上的标准差（选择两个较大的标准差）。 在这种情况下，平均值几乎较小的任务几乎在所有时间都明显更快，如图1所示：

图1.均值大于三个标准差意味着明显可区分的性能
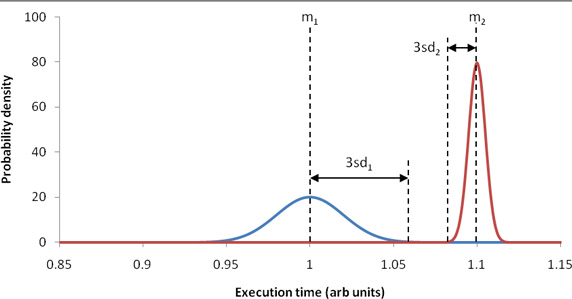
均值大于三个标准差意味着性能明显可区分

不幸的是，更多的两个任务重叠（例如，如果均值相差一个标准差），则确定变得棘手，如图2所示：

图2.均值小于三个标准差意味着性能重叠
平均值相差少于三个标准差意味着性能重叠

也许您所能做的就是按照其任务对两个任务进行排名，但要注意它们有多少重叠，并指出结论中相应的弱点。

可靠性

要解决的另一个问题是这些均值和标准差统计数据本身的可靠性如何。 显然，它们是根据测量结果计算得出的，因此一组新的测量结果可能会产生不同的值。 现在假设测量过程有效。 （注意：可能无法测量“真实的”标准偏差。请参阅文章补充中的“ 标准偏差测量问题”部分，其中探讨了此问题。）然后，如果重复执行该步骤，则平均值和标准偏差有何不同？ 一系列新的测量结果会产生明显不同的结果吗？

回答这些问题的最直观的方法是为统计数据构建置信区间 。 与该统计信息的单个计算值（ 点估计 ）相比，置信区间是估计范围。 称为置信度的概率p与此范围相关。 最常见的是，p被选择为95％，并在置信区间比较期间保持恒定。 置信区间很直观，因为它们的大小表示可靠性：短区间表示该统计信息是精确已知的，而宽区间表示不确定性。 例如，如果任务A的平均执行时间的置信区间为[1，1.1]毫秒，而任务B的平均时间的置信区间为[0.998，0.999]毫秒，则B的均值比A的确定度更高，并且也明显较小（在置信度上）。 有关更多讨论，请参见本文补充中的“ 置信区间”部分。

从历史上看，仅可以针对一些常见的PDF（例如高斯）和简单的统计信息（例如平均值）轻松计算置信区间。 但是，在1970年代后期，开发了一种称为引导的技术。 这是产生置信区间的最佳通用技术。 它适用于任何统计数据，而不仅仅是平均值等简单统计数据。 此外，引导的非参数形式不对基础PDF进行任何假设。 它永远不会产生非实际的结果（例如，置信区间下限的负执行时间），并且与错误地假设PDF（例如高斯）相比，它可以产生更窄和准确的置信区间。 关于引导的细节不在本文讨论范围之内，但是我下面讨论的框架包括一个名为Bootstrap的类，它可以执行计算。 有关更多信息，请参见其Javadocs和源代码（请参阅参考资料 ）。

总之，您必须：

  • 执行许多基准测试。
  • 根据测量结果，计算平均值和标准偏差。
  • 使用这些统计数据来确定两个任务在速度上有明显区别（均值大于三个标准差），或者它们是重叠的。
  • 计算平均值和标准偏差的置信区间，以表明它们的可靠性。
  • 依靠自举是计算置信区间的最佳方法。

框架介绍

到目前为止，我已经讨论了基准测试Java代码的一般原理。 现在，我介绍一个“运行就绪”的基准框架，该框架解决了许多这些问题。

项目

从本文的随附站点下载项目ZIP文件（请参阅参考资料 ）。 ZIP文件包含源文件和二进制文件，以及简单的构建环境。 将内容提取到任何目录中。 有关更多详细信息，请查阅顶级readMe.txt文件。

API

该框架的基本类称为Benchmark 。 这是大多数用户需要查看的唯一类； 其他一切都是辅助的。 大多数用途的API很简单：您将要基准化的代码提供给Benchmark构造函数。 然后，基准测试过程是全自动的。 通常，您唯一要做的后续步骤是生成结果报告 。

任务代码

显然，您必须具有一些要对其执行时间进行基准测试的代码。 唯一的限制是代码必须包含在Callable或Runnable 。 否则，目标代码可以是用Java语言表示的任何内容，从独立的微基准到调用完整应用程序的代码。

将您的任务编写为Callable通常更方便。 Callable.call使您可以抛出已检查的Exceptions ，而Runnable.run强制您实施Exception处理。 而且，正如我在第1部分的死代码消除（DCE）部分中所述，使用Callable防止DCE的运行比Runnable容易得多。 将您的任务编写为Runnable的一个好处是，它可以最大程度地减少对象创建和垃圾回收的开销。 有关详细信息，请参见本文补充中的任务代码：可调用与可运行 。

结果报告

获取基准结果报告的最简单方法是调用Benchmark.toString方法。 此方法仅产生最重要结果和警告的单行摘要报告。 您可以通过调用Benchmark.toStringFull方法获得详细的多行报告，其中包含所有结果和完整说明。 否则，您可以调用Benchmark各种访问器来生成自定义报告。

警告事项

Benchmark尝试诊断一些常见问题，并在检测到此类问题时在结果报告中警告用户。 警告包括：

  • 度量值太低 ：第1部分中的资源回收部分描述了Benchmark如何确定未完全考虑垃圾收集和对象完成成本的情况下发出警告。
  • 离群值和序列相关性 ：执行时间测量值经过离群值和序列相关性统计测试。 离群值表明发生了重大的测量误差。 例如，如果在测量过程中计算机上开始了其他活动，则会出现较大的异常值。 较小的异常值可能暗示发生了DCE。 串行相关性表明JVM尚未达到其稳态性能配置文件（应以具有很小随机变化的执行时间为特征）。 具体而言，正序列相关性指示趋势（向上或向下），负序列相关性指示均值回归（例如，振荡执行时间）； 都不是好看的。
  • 标准偏差不正确 ：有关详细信息，请参见文章补充中的“ 标准偏差警告”部分。

简单的例子

清单1中的代码片段说明了本节到目前为止我所讨论的要点：

清单1.第35个斐波那契数的基准计算 
public static void main(String[] args) throws Exception {
    Callable<Integer> task = 
        new Callable<Integer>() { public Integer call() { return fibonacci(35); } };
    System.out.println("fibonacci(35): " + new Benchmark(task));
}

protected static int fibonacci(int n) throws IllegalArgumentException {
    if (n < 0) throw new IllegalArgumentException("n = " + n + " < 0");
    if (n <= 1) return n;
    return fibonacci(n - 1) + fibonacci(n - 2);
}

在清单1中， main将要作为基准的代码定义为Callable ，并将其简单地提供给Benchmark构造函数。 这个Benchmark构造函数多次执行一个任务，首先确保代码预热 ，然后收集执行统计信息。 构造函数返回后，它所在的代码上下文（即在println ）导致对新Benchmark实例的toString方法的隐式调用，该方法报告基准的摘要统计信息。 使用Benchmark通常很简单。

在我的配置中，我得到以下结果： 

fibonacci(35): first = 106.857 ms, mean = 102.570 ms (CI deltas: -35.185 us, 
+47.076 us), sd = 645.586 us (CI deltas: -155.465 us, +355.098 us) 
WARNING: execution times have mild outliers, SD VALUES MAY BE INACCURATE

解释：

  • 第一次调用fibonacci(35)时，执行时间为106.857毫秒。
  • 执行时间平均值的点估计为102.570毫秒。 平均值的95％置信区间约为点估计值的-35 / + 47微秒，即[102.535，102.617]毫秒，相对较窄，因此可以放心地知道平均值。
  • 执行时间的标准偏差的点估计为645.586微秒。 标准偏差的95％置信区间大约是点估计值的-155 / + 355微秒，即[490.121，1000.684]μs，它相对较宽，因此已知的置信度要低得多。 实际上，最后的警告表明标准偏差未正确测量 。
  • 结果还警告离群值。 在这种情况下，它们是可忽略的，但是如果您担心，可以使用Benchmark的toStringFull方法重新运行代码，该方法将列出所有违规者的值，从而使您可以进行判断。

数据结构访问时间

Benchmark可以比较几种常见数据结构的访问时间，这些Benchmark可以更好地说明基准问题以及如何使用Benchmark来解决这些问题。

仅仅测量数据结构的访问时间是一个真正的微基准。 当然，许多注意事项也适用于微基准测试。 （例如，它们可能无法指示整个应用程序的运行情况。）但是这里的测量值可以自我补偿，因为它们很难准确地执行操作，并且因为出现了许多有趣的问题（例如缓存效果），使它们成为一个很好的例子。 。

考虑清单2中的代码，该代码对数组访问时间进行了基准测试（其他数据结构的代码看起来类似）：

清单2.数组访问基准测试代码 
protected static Integer[] integers;    // values are unique (integers[i] <--> i)

protected static class ArrayAccess implements Runnable {
    protected int state = 0;
    
    public void run() {
        for (int i = 0; i < integers.length; i++) {
            state ^= integers[i];
        }
    }
    
    public String toString() { return String.valueOf(state); }
}

理想情况下，代码除了访问integers数组之外什么都不做。 但是，为了方便地访问integers所有元素，我使用了一个循环，该循环在基准测试中引入了寄生循环开销。 请注意，我使用的是老式的显式int循环，而不是for循环增强的for (int i : integers)更为方便，因为它甚至对数组来说速度也更快（请参阅参考资料 ）。 我在这里使用的循环应该是次要的缺陷，因为任何不错的即时（JIT）编译器都会执行循环展开，从而减少了影响。

但是，更严重的是防止DCE所需的代码。 首先，为任务类选择了Runnable ，因为如前所述，它可以最大程度地减少对象创建和垃圾回收开销，这对于此类轻量级微基准测试至关重要。 其次，假定此任务类是Runnable ，则需要将数组访问的结果分配给state字段（并且state必须在覆盖的toString方法中使用）以防止DCE。 第三，我将数组访问与state的先前值按位进行XOR，以确保执行每个访问。 （仅执行state = integers[i]可能会触发智能编译器认识到可以跳过整个循环，而只需执行state = integers[integers.length - 1] 。）这四个附加操作（字段读取，自动拆箱将Integer转换为int ，按位XOR，字段写入）是不可避免的开销，这会破坏基准： 实际上，它所测量的不仅仅是数组访问时间 。 所有其他数据结构基准测试也都失去了光泽，尽管对于访问时间相对较长的数据结构而言，相对影响可以忽略不计。

图3和图4给出了我常用的台式机配置中两种不同大小的integers访问时间的结果：

图3.数据结构访问时间（案例：1024个元素）
图3.数据结构访问时间（案例：1024个元素）
图4.数据结构访问时间（案例：1024×1024元素）
图4.数据结构访问时间（案例：1024×1024元素）

对结果的评论：

  • 仅显示平均执行时间的点估计。 （均值的置信区间总是非常紧密-典型宽度是均值的〜1000倍-不会显示在这些图表上。）
  • 所有这些基准测试仅使用一个线程。 同步的类没有线程争用。
  • 清单2中已经介绍了数组元素访问（非同步）代码。
  • 数组元素访问（同步）代码是相同的，除了循环体是： synchronized (integers) { state ^= integers[i]; } synchronized (integers) { state ^= integers[i]; }
  • 图3和4中ConcurrentHashMap情况1与情况2之间的区别仅在于所使用的ConcurrentHashMap构造函数中：情况1指定concurrencyLevel = 1 ，情况2使用默认值（为16）。 因为所有这些基准测试仅使用一个线程，所以情况1应该稍微快一些。
  • 每个基准都有一个或多个警告：
    • 几乎所有的数据都有异常值，但是似乎没有一个异常值如此之大，以至于它们的存在会极大地影响结果。
    • 所有1024×1024元素结果都具有序列相关性。 目前尚不清楚这是一个多大的问题。 1024个元素的结果中没有一个具有序列相关性。
    • 标准偏差始终无法测量（典型的微基准）。

这些结果可能就是您所期望的：不同步的数组访问是最快的数据结构。 ArrayList位居第二，几乎与原始数组一样快。 （大概服务器JVM在内联直接访问其底层数组方面做得非常出色。）它比同步但在其他方面相似的Vector快得多。 第二快的数据结构是HashMap ，其后是ThreadLocal （本质上是专门的哈希表，其中当前线程是键）。 确实，在这些测试中， HashMap速度几乎与Vector一样快，直到您考虑将Integers用作键，并且它们具有特别快的hashCode实现（它只是返回int值）之后， HashMap才令人印象深刻。 接下来是ConcurrentHashMap案例，其次是所有结构中最慢的TreeMap 。

尽管此处未显示结果，但我在完全不同的机器上进行了相同的基准测试（使用SunOS asm03 5.10在1.167GHz上运行32GB RAM的SPARC-Enterprise-T5220；与台式机相同的JVM版本和设置使用，但是我现在配置了Benchmark来测量CPU时间，而不是经过的时间，因为测试都是单线程的，Solaris很好地支持了这一点。 相对结果与上述相同。

我上面介绍的结果中唯一的主要异常是同步数组访问时间：我本以为它们可以与Vector相提并论，但是它们的速度始终慢三倍以上。 最好的猜测是：一些与锁相关的优化（例如锁省略或锁偏置）无法启动（请参阅参考资料 ）。 这种猜测似乎已被以下事实证实了：使用自定义锁定优化的Azul JVM中不存在此异常。

一个较小的异常情况是，在使用1024×1024元素时， ConcurrentHashMap情况1仅比情况2快，而在使用1024个元素时，实际上稍慢一些。 此异常可能是由于不同数量的表段的较小的内存放置效果所致。 这种效果在T5220盒子上不存在（情况1总是比情况2快一点，而不管元素的数量如何）。

HashMap性能相对于ConcurrentHashMap更快，这并非异常。 两种情况下的代码都类似于清单2 ，只是state ^= integers[i]被state ^= map.get(integers[i])代替。 integers的元素按顺序出现（ integers[i].intValue() == i ），并以相同的顺序作为键提供。 事实证明，与ConcurrentHashMap相比， HashMap中的哈希预处理功能具有更好的顺序缓存局部性（因为ConcurrentHashMap需要更好的高位扩展）。

这就引出了一个有趣的观点：上面给出的结果在多大程度上取决于integers按顺序迭代的事实？ 可能存在某些数据结构比其他数据结构受益更多的内存局部性影响吗？ 为了回答这些问题，我重新运行了这些基准测试，但选择了随机的integers元素而不是顺序的元素。 （我通过使用软件线性反馈移位寄存器来生成伪随机值来完成此操作；请参阅参考资料 。它为每个数据结构访问增加了大约3纳秒的开销。）图5显示了1024×1024个integers元素的结果。 ：

图5.数据结构访问时间（大小：1024×1024元素，随机访问）
图3.数据结构访问时间（案例：1024个元素）

您可以看到，与图4相比， HashMap现在具有与ConcurrentHashMap相同的性能（正如我认为的那样）。 TreeMap具有令人震惊的随机访问。 array和ArrayList数据结构仍然是最好的，但是它们的相对性能已经下降（它们各自的随机访问性能大约差10倍，而ConcurrentHashMap随机访问性能大约只有差两倍）。

还有一点：图3、4和5绘制了各个访问时间。 例如，从图3中可以看到，从TreeMap访问单个元素的时间TreeMap 80纳秒。 但是这些任务看起来都像清单2所示 ； 也就是说，每个任务在内部执行多个数据访问（也就是说，它们遍历每个integers元素）。 如何从包含多个相同动作的任务中提取单个动作统计信息？

我在清单2中遗漏的是父代码，它显示了如何处理此类任务。 您可以使用清单3所示的代码：

清单3.具有多个动作的任务的代码 
public static void main(String[] args) throws Exception {
    int m = Integer.parseInt(args[0]);

    integers = new Integer[m];
    for (int i = 0; i < integers.length; i++) integers[i] = new Integer(i);
    
    System.out.println(
        "array element access (unsynchronized): " + new Benchmark(new ArrayAccess(), m));
    // plus similar lines for the other data structures...
}

在清单3中，我使用Benchmark构造函数的两个参数版本。 清单3中以粗体显示的第二个参数指定任务组成的相同动作的数量，在这种情况下，为m = integers.length 。 有关更多详细信息，请参见文章补充中的阻止统计与操作统计部分。

最优投资组合计算

到目前为止，在本文中，我仅考虑了微基准测试。 尽管它们可能很有趣，但是衡量真实应用程序的性能才是基准测试的真正用途所在。

Markowitz平均方差投资组合优化是您中很多投资者可能感兴趣的一个示例，这是财务顾问用来构建具有较高风险/回报特征的投资组合的标准技术（请参阅参考资料 ）。

一个公司，提供一个Java库做这些计算是WebCab组件（见相关主题 ）。 清单4中的代码对它的Portfolio v5.0（J2SE版）库在解决有效边界方面的性能进行了基准测试（请参阅参考资料 ）：

清单4.投资组合优化基准测试代码 
protected static void benchmark_efficientFrontier(
    double[][] rets, boolean useCons, double Rf, double scale
) throws Exception {
    Benchmark.Params params = new Benchmark.Params(false);    // false to meas only first
    params.setMeasureCpuTime(true);
    
    for (int i = 0; i < 10; i++) {
        double[][] returnsAssetsRandomSubset = pickRandomAssets(rets, 30);
        Callable<Double. task = new EfTask(returnsAssetsRandomSubset, useCons, Rf, scale);
        System.out.println(
            "Warmup benchmark; can ignore this: " + new Benchmark(task, params) );
    }
    
    System.out.println();
    System.out.println("n" + "\t" + "first" + "\t" + "sharpeRatioMax");
    for (int n = 2; n <= rets.length; n++) {
        for (int j = 0; j < 20; j++) {    // do 20 runs so that can plot scatter
        double[][] returnsAssetsRandomSubset = pickRandomAssets(rets, n);
        Callable<Double> task = new EfTask(returnsAssetsRandomSubset, useCons, Rf, scale);
        Benchmark benchmark = new Benchmark(task, params);
        System.out.println(
            n + "\t" + benchmark.getFirst() + "\t" + benchmark.getCallResult());
        }
    }
}

因为这是一篇有关基准测试的文章，而不是有关投资组合理论的文章，​​所以清单4省略了EfTask内部类的代码。 （换句话说： EfTask获取资产历史收益数据，从中计算出预期收益和协方差，沿着有效边界求解50个点，然后返回具有最大Sharpe比率的点；请参阅参考资料 。最佳Sharpe比率是1测量特定资产组的最佳投资组合的质量，并在经过风险调整的基础上确定最佳回报。有关详细信息，请参见本文代码下载中的相关源文件。）

该代码的目的是根据资产数量同时确定执行时间和投资组合质量，这对于进行投资组合优化的人可能是有用的信息。 清单4中的n循环进行了此确定。

该基准测试提出了一些挑战。 首先，计算可能需要很长时间，尤其是在考虑大量资产时。 因此，我避免使用像new Benchmark(task)这样的简单代码，该代码可以执行60次测量（默认情况下）。 相反，我选择创建一个自定义Benchmark.Params实例，该实例指定仅应执行一次测量。 （它还指定应该进行CPU时间测量，而不是默认的经过时间，只是为了说明如何实现。这里可以这样做，因为WebCab组件库不会在这种情况下创建线程。） ，在执行这些单个测量基准中的任何一个基准之前， i循环会执行几个一次性基准，以让JVM首先完全优化代码。

其次，通常的结果报告不足以满足该基准测试的需求，因此我生成了一个定制的报告 ，该报告应仅提供制表符分隔的数字，以便可以轻松地将其复制并粘贴到电子表格中以进行后续图形显示。 因为只进行一次测量，所以使用Benchmark的getFirst访问器方法来检索执行时间。 给定资产集的最大Sharpe比率是Callable任务的返回值。 它是通过Benchmark的getCallResult访问器方法获取的。

此外，我想对结果中的分散情况进行可视化表示，因此对于给定数量的资产，内部j循环执行每个基准测试20次。 这就是导致下图中的每资产数量20个点的原因。 （在某些情况下，这些点重叠得太多，以致看起来只有几个点存在。）

关于结果。 我使用的资产是当前OEX（S＆P 100）指数中的股票。 我将过去三年（2005年1月1日至2007年12月31日）的每周资本收益用作历史收益。 股息被忽略（如果包括在内，它们会略微提高夏普比率）。

图6是执行时间与资产数量的关系图：

图6.投资组合优化执行时间
图6.投资组合优化执行时间

因此，执行时间随着资产数量的增加而呈三次方增长。 这些度量中的分散是真实的，并非基准错误：投资组合优化的执行时间取决于所考虑资产的类型。 特别是，某些类型的协方差可能需要非常仔细的（小步长）数值计算，这会影响执行时间。

图7是投资组合质量（最大夏普比率）与资产数量的关系图：

图7.投资组合质量
图7.投资组合质量

夏普比率的最大值最初有所提高，但很快就停止增加，大约为15到20。 此后，唯一的效果是，随着资产数量的增加，价值范围会缩小到最大。 这种影响也是真实的：之所以发生，是因为随着所考虑的资产数量的增加，您拥有所有“热门”资产（将主导最优投资组合）的几率稳定在100％。 请参阅本文补充中的“ 投资组合优化”部分，以获取更多本文范围之外的想法。

最后警告

微基准测试应反映实际用例。 例如，我选择衡量数据结构的访问时间是因为JDK集合的设计预期是典型的应用程序会混合执行约85％的读取/遍历，14％的添加/更新和1％的删除。 但是，请注意，更改这些混合物可能导致相对性能几乎任意不同。 另一个潜在的危险是类层次结构的复杂性：微基准通常使用简单的类层次结构，但是方法调用开销在复杂的类层次结构中可能变得很重要（请参阅参考资料 ），因此准确的微基准必须反映现实。

确保基准测试结果相关。 提示：将StringBuffer与StringBuilder可能不会告诉您Web服务器的性能。 更高级别的架构选择（不适合进行微基准测试）可能更为重要。 （尽管您无论如何应该在几乎所有代码中自动使用ArrayList/HashMap/StringBuilder ，而不是较早的Vector/Hashtable/StringBuffer 。）

注意仅依靠微基准测试。 例如，如果要确定一种新算法的效果，则不仅要在基准环境中进行测量，还要在实际应用场景中对其进行测量，以查看它是否真正起到了很大作用。

显然，只有在测试了合理的计算机和配置示例后，您才能得出一般的性能结论。 不幸的是，一个典型的错误是仅在开发计算机上进行基准测试，并假定对运行代码的所有计算机都具有相同的结论。 如果您想更全面，则需要多个硬件，甚至需要不同的JVM（请参阅参考资料 ）。

不要忽略分析。 使用各种性能分析工具来运行基准测试，以确认其行为符合预期（例如，大部分时间都花在了您认为应该是关键方法上的时间）。 这也可以确认DCE不会使您的结果无效。

归根结底，没有什么可替代的是真正了解事物的低水平运行以得出合理的结论。 例如，如果您想查看Java语言的正弦实现（ Math.sin ）是否比C更快，您可能会发现在x86硬件上Java的正弦要慢得多。 这是因为Java正确地避免了快速但不准确的x86硬件帮助程序指令。 无视此基准的人得出的结论是，当C真正确定的是专用（但不准确）的硬件指令比精确的软件计算要快时，C的速度比Java语言要快得多。

结论

基准测试通常需要执行许多测量并使用统计数据来解释结果。 本文介绍的基准测试框架支持这些功能并解决了许多其他问题。 无论您使用此框架，还是按照本系列两部分所介绍的材料进行指导，创建自己的框架，您现在都可以更好地帮助确保Java代码高效地执行。

翻译自: https://www.ibm.com/developerworks/java/library/j-benchmark2/index.html

cusi77914
关注
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值