哈萨克斯坦公司股价的VaR和ConVaR估计

The last decades the world economy regularly falls into this vortex of financial crises that have affected each country. It almost led to the collapse of the existing financial system, due to this fact, experts in mathematical and economic modelling have become to use methods for controlling the losses of the asset and portfolio in the financial world (Lechner, L. A., and Ovaert, T. C. (2010). There is an increasing trend towards mathematical modelling of an economic process to predict the market behaviour and an assessment of its sustainability (ibid). Having without necessary attention to control and assess properly threats, everybody understands that it is able to trigger tremendous cost in the development of the organisation or even go bankrupt.

在过去的几十年中，世界经济经常陷入影响每个国家的金融危机漩涡。 由于这个事实，这几乎导致了现有金融体系的崩溃，数学和经济建模方面的专家已开始使用控制金融世界中资产和投资组合损失的方法(洛杉矶的Lechner和TC的Ovaert (2010)。对经济过程进行数学建模以预测市场行为并对其可持续性进行评估的趋势正在增加(同上)。由于无需对控制和正确评估威胁进行必要的关注，每个人都知道它能够触发组织发展的巨大成本，甚至破产。

Value at Risk (VaR) has eventually been a regular approach to catch the risk among institutions in the finance sector and its regulator (Engle, R., and Manganelli S., 2004). The model is originally applied to estimate the loss value in the investment portfolio within a given period of time as well as at a given probability of occurrence. Besides the fact of using VaR in the financial sector, there are a lot of examples of estimation of value at risk in different area such as anticipating the medical staff to develop the healthcare resource management Zinouri, N. (2016). Despite its applied primitiveness in a real experiment, the model consists of drawbacks in evaluation, (ibid).

风险价值(VaR)最终已成为在金融部门的机构及其监管机构中捕捉风险的常规方法(Engle，R。和Manganelli S.，2004)。 该模型最初用于估计给定时间段内和给定出现概率下投资组合中的损失值。 除了在金融部门使用VaR的事实外，还有许多在不同领域评估风险价值的例子，例如期望医护人员发展医疗资源管理Zinouri，N.(2016)。 尽管在实际实验中应用了原始性，但该模型仍存在评估缺陷(同上)。

The goal of the report is a description of the existing VaR model including one of its upgrade versions, namely, Conditional Value at Risk (CVaR). In the next section and section 3, the evaluation algorithm and testing of the model are explained. For a vivid illustration, the expected loss is estimated on the asset of one of the Kazakhstani company trading in the financial stock exchange market in a long time period. The final sections 4 and 5 discuss and demonstrate the findings of the research work.

该报告的目的是描述现有VaR模型，包括其升级版本之一，即条件风险值(CVaR)。 在下一部分和第3部分中，将说明模型的评估算法和测试。 为了生动地说明这一点，预期损失是根据哈萨克斯坦一家公司在很长时间内在金融证券交易所市场上交易的资产估算的。 最后的第4和第5节讨论并演示了研究工作的结果。

背景 (Background)

It is believed that the first usage of the VaR by the giant financial organisations up to 40 years ago and in consequence VaR has become popular among other trading firms, even financial regulators have had attention to the model (Linsmeier, T. J., and Pearson, N. D. 2000). For instance, the U.S. Securities and Exchange Commission inscribed VaR on a list of quantitative methods for calculating the market risk and property in 1997 (ibid).

据信，直到40年前，大型金融机构才首次使用VaR，因此VaR在其他贸易公司中也很流行，甚至金融监管机构也对该模型有所关注(Linsmeier，TJ和Pearson，ND 2000)。 例如，美国证券交易委员会在1997年用VaR列出了用于计算市场风险和财产的定量方法清单(同上)。

Actually, according to articles of Lechner, L. A., and Ovaert, T. C. (2010) as well as Linsmeier, T. J., and Pearson, N. D. (2000), VaR is an estimating equation expressed in monetary units which do not exceed the loss in magnitude range during a given time period and given confidence level. Typically, the confidence level of the model estimation (99%, 97.5%, 95%) or in other words the probability that some unfavourable case will have happened and influence on the market are equal to 1, 2.5 and 5 percent (ibid).

实际上，根据路易斯安那州Lechner和TC的Ovaert(2010)以及Ts的Linsmeier和ND的Pearson(2000)的文章，VaR是一个以货币单位表示的估计方程，不会超过损失幅度范围在给定的时间段和给定的置信度下。 通常，模型估计的置信度(99％，97.5％，95％)，或者换句话说，发生某些不利情况并对市场产生影响的概率等于1、2.5和5％(同上)。

The well-known equation of the VaR is able to be described (Phelps S, 2018):

可以描述著名的VaR方程(Phelps S，2018)：

Where X is a random variable that performs the amount of the portfolio’s value, and is a cumulative distribution function (ibid).

其中X是执行投资组合价值总额的随机变量，并且是累积分布函数(同上)。

On the other hand, Hooper G.P. (1996, cited in Lechner, L. A., and Ovaert, T. C. 2010) denotes VaR with confidence alpha defines in a quite elementary way:

另一方面，Hooper GP(1996年，引用于洛杉矶Lechner和Ovaert，TC 2010年引用)用非常基本的方式表示了具有置信度alpha定义的VaR：

Where is the standard deviation of selected stock returns, is the square root of the fixed time period and is the cumulative distribution function (CDF) for a normal distribution (Lechner, L. A., and Ovaert, T. C. 2010).

哪里 是选定股票收益的标准差， 是固定时间段的平方根，并且 是正态分布的累积分布函数(CDF)(Lechner，LA和Ovaert，TC 2010)。

Although VaR is a well-known and handled method to estimate decided portfolio risk, there are shortcomings in a case when measuring vulnerability to ultimate market issues, namely, the example is related to the probability of extreme market events is not adequately caught in the tail of the normal distribution (Capiński, M. J. 2015). To solve this issue, the Conditional Value at Risk (CVaR) was created which consider the expected value of loss instead of VaR (ibid). CVaR defines as:

尽管VaR是估算已确定的投资组合风险的众所周知且易于处理的方法，但在衡量对最终市场问题的脆弱性的情况下仍存在缺陷，即该示例与极端市场事件未充分抓住尾巴的可能性有关正态分布(Capiński，MJ 2015)。 为了解决此问题，创建了“条件风险值”(CVaR)，其中考虑了预期的损失损失值而不是VaR(同上)。 CVaR定义为：

Where Ahn D.-H. et.al (1999, cited in Capiński, M. J. 2015) interpret as VaR of X random variable (return of a stock price) with probability and defines as the upper quantile of X.

哪里安D.-H. et.al(1999，Capiński，MJ 2015引用)解释 X概率的X变量的VaR 并定义为X的上分位数。

Moreover, Acerbi C. and Tasche D. (2002, cited in Capiński, M. J. 2015) confirm, “The CVaR is a coherent risk measure”. Rockafellar, R. T., and Uryasev, S. (2000) notice that CVaR has extra features: transition-equivariant, positively homogeneous, convex and etc.

此外，Acerbi C.和Tasche D.(2002年，Mapi，Capiński引用，2002年)确认：“ CVaR是一种连贯的风险衡量”。 Rockafellar，RT和Uryasev，S.(2000)注意到CVaR具有额外的功能：等价跃迁，正均匀，凸等。

The following chapter of the article demonstrates the implementation of wellknown Value at Risk (VaR) and Conditional Value at Risk (CVaR) also announced as Expected shortfall (ES) noticed in the work of Rockafellar, R. T., and Uryasev, S. (2000) by using information technology on real data.

本文的下一章演示了Rockafellar，RT和Uryasev，S.(2000)的工作中还宣布的众所周知的风险价值(VaR)和条件风险价值(CVaR)的实现，它们也被宣布为“预期缺口(ES)”。通过对真实数据使用信息技术。

方法 (Methodology)

Let consider the most commonly used methods for calculating VaR, as well as its advantages and disadvantages.

让我们考虑最常用的计算VaR的方法，以及它的优缺点。

According to the report of Lechner, L. A., and Ovaert, T. C. (2010), the historical simulation is a widespread approach to evaluate VaR and its modification. In historical modelling of the data, we take the values of financial fluctuations for the portfolio which are already known from past measurements. It is therefore only logical sequence that the disadvantage of this method is the impossibility of building predictions for portfolios without a piece of information about it. The Monte Carlo method is in many ways identical to the method of historical modelling that used for high-accurate technique, the main clear difference that the calculation of Monte Carlo simulation is not based on real data, but realized on randomly generated values. The advantage of this method is the possibility of considering as a large number of situations, and emulating market behaviour in extreme conditions as well as there is no need an approximation between risk factors and changes in a portfolio (Glasserman, P., Heidelberger, P. and Shahabuddin, P., 2002). The obvious drawback is the large computational resources required to implement this approach (ibid).

根据Lechner，LA和Ovaert，TC(2010)的报告，历史模拟是评估VaR及其修改的广泛方法。 在数据的历史建模中，我们采用了从过去的测量中已经知道的投资组合的财务波动值。 因此，只有逻辑上的顺序是该方法的缺点是不可能在没有任何信息的情况下为投资组合建立预测。 蒙特卡洛方法在许多方面与用于高精度技术的历史建模方法相同，主要的明显区别在于蒙特卡洛模拟的计算不是基于真实数据，而是基于随机生成的值。 这种方法的优点是可以考虑多种情​​况，并在极端条件下模拟市场行为，并且无需在风险因素和投资组合变化之间进行近似估算(Glasserman，P.，Heidelberger，P和Shahabuddin，P.，2002年)。 明显的缺点是实现此方法所需的大量计算资源(同上)。

Naturally, these are not the only these methods for calculating VaR models. In addition, there are both simple linear and quadratic models of price prediction, and a rather complicated method of variations, which were not covered in the essay.

当然，这些并不是计算VaR模型的唯一方法。 此外，价格预测有简单的线性模型和二次模型，还有相当复杂的价格变动方法，本文中并未介绍。

数据分析 (Data analysis)

As secondary data for testing the accurate estimation, the stock of KAZ Minerals is taken. To be clarified the work, the Adjusted closed price is taken for simulation in a model. The shares of KAZ Minerals company (KAZ.L) is one the successfully trading securities among Kazakhstani firms on the London Stock Exchange (LSE) as well as categorized in Premium Equity Commercial Companies list (London Stock Exchange, 2019). The entity presents itself as the massive copper mining company in Kazakhstan (Kazminerals.com. 2019).

作为检验准确估计的辅助数据，将使用KAZ Minerals的库存。 为了澄清工作，在模型中采用调整后的收盘价进行模拟。 KAZ Minerals公司(KAZ.L)的股票是哈萨克斯坦公司在伦敦证券交易所(LSE)上成功交易的证券之一，并且归类于高级股权商业公司名单(London Stock Exchange，2019)。 该实体表示自己是哈萨克斯坦的大型铜矿开采公司(Kazminerals.com.2019)。

The historical data of the share price is downloaded from Yahoo Finance web site (Finance.yahoo.com, 2019). To ensure the validity of the work, the period of one year from 22 March 2018 to 22 March 2019 is observed. Furthermore, to avoid the information disruption, in the analysis, the historical data of the KAZ.L share price is downloaded in Comma-Separated Values (CSV) format due to the fact that the CSV format is compatible by Microsoft Excel program (Excel). The chosen data of the project is presented as a line graph by using Excel in Figure 1.

股价的历史数据可从Yahoo Finance网站(Finance.yahoo.com，2019)下载。 为确保工作的有效性，遵守了从2018年3月22日至2019年3月22日的一年期限。 此外，为避免信息中断，在分析中，由于Microsoft Excel程序(Excel)兼容CSV格式，因此以逗号分隔值(CSV)格式下载了KAZ.L股价的历史数据。 。 使用图1中的Excel，将项目的所选数据显示为折线图。

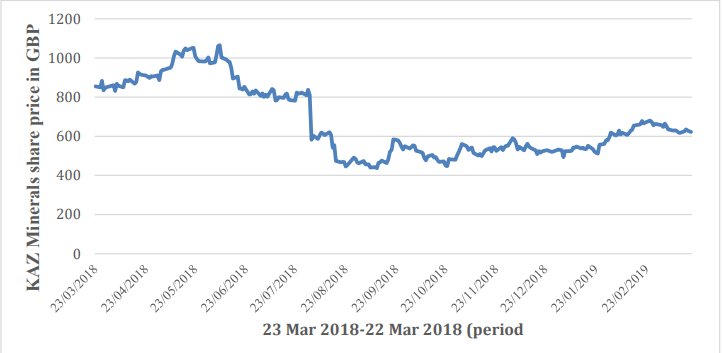
Figure 1. The dynamic of change KAZ Minerals stock price for one year

图1.一年中KAZ Minerals股票价格变化的动态

Owing to the limitation of the report timeline, instead of using a programming language like Python for implementation of assessment models, the data is analysed completely in Excel.

由于报告时间轴的局限性，没有使用像Python这样的编程语言来实现评估模型，而是在Excel中完全分析了数据。

发现 (Findings)

In the previous section, the models to forecast the potential losses in a portfolio based on VaR and CVaR equation and used changes in KAZ Minerals share price from 23 March 2018 to 23 March 2019, downloaded from official web source Yahoo Finance (Finance.yahoo.com, 2019). Both equations executed for each date from the chosen period.

在上一节中，从官方网站Yahoo Finance(Finance.yahoo)下载的模型基于VaR和CVaR方程预测了投资组合的潜在损失，并使用了2018年3月23日至2019年3月23日KAZ Minerals股价的变​​化。 com，2019年)。 这两个方程式针对所选期间的每个日期执行。

Table 1 demonstrates the mean business daily return, a standard deviation of returns, a minimum value of returns and a maximum value of returns for this example.

表1展示了此示例的平均每日业务收益，收益的标准差，收益的最小值和收益的最大值。

Table 1. Share mean return and standard deviation of returns

表1.份额平均收益率和收益率标准差

The corresponding mean is -0.0006 and standard deviation 0.0355 of the returns for the selected unique security KAZ Minerals. What is more that the variance of the returns is 0.0013. Additionally, that should certainly be underlined that in the research work of Vee, D. N. C., and Gonpot, P. N (2014) the Kazakhstani stock returns showed considerable value in volatility however the estimation was related to the index of Kazakhstan Stock Exchange in pre and post period 2008. Also, it should be mentioned that the maximum value among returns is 0.0998, as well as the minimum value among returns is -0.2829 in loss distribution. Table 2 presents the maximum and minimum values among Adjusted close stock price(KAZ.L) in Pound Sterling (GBP) trading in London Stock Exchange from 23 March 2018 to 22 March 2019.

所选的唯一安全性KAZ Minerals的相应平均值为-0.0006，收益率的标准偏差为0.0355，标准偏差为0.0355。 而且收益的方差是0.0013。 此外，应该特别强调的是，在Vee，DNC和Gonpot，P. N(2014)的研究工作中，哈萨克斯坦的股票收益率显示出相当大的波动性，但是估计值与哈萨克斯坦证券交易所早前和之后的指数有关。应当注意，在损失分配中，收益之间的最大值为0.0998，收益之间的最小值为-0.2829。 表2列出了2018年3月23日至2019年3月22日在伦敦证券交易所英镑(GBP)交易中调整后的收盘价(KAZ.L)中的最大值和最小值。

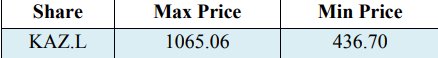
Table 2. The maximum and minimum KAZ Minerals stock price in GBP

表2. KAZ Minerals的最大和最小股价(英镑)

The following step is evaluation Value at Risk (VaR) and Conditional Value at Risk (CVaR) for the confidence level — 0.99, 0.972 and 0.95. The values are revealed in Table 3.

下一步是对置信度0.99、0.972和0.95的评估风险价值(VaR)和条件风险价值(CVaR)。 这些值在表3中显示。

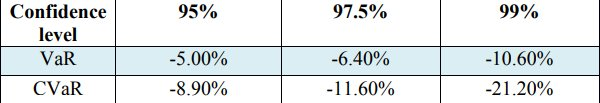
Table 3. VaR and CVaR values of the returns

表3.收益的VaR和CVaR值

The sample size of the simulation is taken 252 units from 23 March 2018 to 22 March 2019 during one year.

在2018年3月23日至2019年3月22日的一年中，抽取了252个模拟样本。

讨论区 (Discussion)

In the report, VaR and CVaR equations demonstrate the credible value in case of the estimation models for a share price of Kazakhstani company in the short-term period. With these values at one hand, both methods present adequate results to assess the value of the threats for investment portfolio (Linsmeier, T. J., and Pearson, N. D. 2000; Lechner, L. A., and Ovaert, T. C. 2010).

在报告中，VaR和CVaR方程在短期模型中证明了哈萨克斯坦公司股价的估计模型的可信值。 一方面，使用这些值，两种方法都可以提供足够的结果来评估投资组合的威胁的价值(Linsmeier，TJ和Pearson，ND 2000； Lechner，LA，Ovaert，TC 2010)。

Moreover, according to findings from Table 2, the next notice is straightforward that the values for CVaR are more massive in comparison with the VaR values by all confidence level measures. It can be given an explanation by the fact the CVaR takes chosen portfolio average risk consequently it is more sensitive on the tail of the loss distribution than VaR. This proves once again that CVaR is a coherent risk (Acerbi C. and Tasche D., 2002, cited in Capiński, M. J. 2015; Rockafellar, R. T., and Uryasev, S. 2000). For example, with regard to the adequacy of both estimation models, with confidence level 99% VaR and CVaR illustrate the significant per cent of loss from returns of the stock. To be precise, it might be detected VaR is -10.60% and CVaR is -21.20%. It is pretty clear the reason of the colossal measures of CVaR with a given confidence level 99% due to the fact the range of stock price during the period, the maximum price is 1065.06 GBP minimum stock price is 436.70 GBP, respectively.

而且，根据表2的发现，接下来的通知很直接，即与所有置信度度量相比，VaR值比CVaR值更大。 CVaR承担选择的投资组合平均风险的事实可以对此作出解释，因此，与VaR相比，CVaR在损失分布的尾部更加敏感。 这再次证明了CVaR是一个连贯的风险(Acerbi C.和Tasche D.，2002，在Capiński，MJ 2015中引用； Rockafellar，RT和Uryasev，S.2000)。 例如，关于两个估计模型的充分性，置信水平为99％，VaR和CVaR说明了股票收益损失的显着百分比。 准确地说，可能检测到VaR为-10.60％，CVaR为-21.20％。 很清楚，在给定置信度99％的情况下，采取CVaR之所以采取巨大措施的原因是由于该期间的股价范围，最高价格分别为1065.06英镑，最低股价分别为436.70英镑。

结论 (Conclusion)

Having considered everything above, it should be obviously mentioned again that the aim of the report is to demonstrate the estimation of the value of possible loss for Kazakhstani company (KAZ Minerals) over a period from 23 March 2018 to 22 March 2019. The evaluation methods formed on Value at Risk (VaR) and Conditional Value at Risk (CVaR) equations. The performances from the simulation are compared to each other in the same time period. The results show the significant value for each method and prove the previous work on the same area that CVaR has more accurate measures in comparison with VaR (Acerbi C. and Tasche D., 2002, cited in Capiński, M. J. 2015; Rockafellar, R. T., and Uryasev, S.2000).

考虑了上述所有内容后，显然应该再次提到，该报告的目的是证明哈萨克斯坦公司(KAZ Minerals)在2018年3月23日至2019年3月22日期间可能损失的价值估算。评估方法由风险价值(VaR)和条件风险价值(CVaR)等式形成。 将模拟的性能在同一时间段内相互比较。 结果显示了每种方法的重要价值，并证明了以前在同一领域开展的工作，与VaR相比，CVaR具有更准确的测量方法(Acerbi C.和Tasche D.，2002，引自Capiński，MJ 2015; Rockafellar，RT，和Uryasev，S.2000)。

Despite criticism, VaR a widespread tool in all financial institutions to present day and there are a wide range of its modification version. Owing to the obstacles of the complex calculation in the deep research, the experiment is done by using Microsoft Excel instead of using a programming language like Python, as well as the results are revealed in the report. The results of the essay are able to be a basement for further work in using complex estimation measure of risk for the portfolio in the stock exchange industry, the insurance industry and investment industry.

尽管存在批评，但VaR至今仍是所有金融机构中广泛使用的工具，其修改版本范围很广。 由于深入研究中复杂计算的障碍，该实验是通过使用Microsoft Excel而不是使用Python之类的编程语言来完成的，并且结果在报告中有所披露。 本文的结果可以为在证券交易业，保险业和投资业中对投资组合使用复杂的风险评估方法进行进一步工作奠定基础。

Reference 参考

Capiński, M. J. (2015). Hedging conditional value at risk with options. European Journal of Operational Research, 242(2), 688-691.

卡宾斯基，MJ(2015)。 使用期权对冲条件价值风险。 欧洲运筹学杂志，242(2)，688-691。

Engle, R. and Manganelli, S. (2004). CAViaR Conditional Value at Risk by Quantile Regression. Journal of Business & Economic Statistics, American Statistical Association, 22, 367-381.

Engle，R.和Manganelli，S.(2004)。 CAViaR分位数回归有风险的条件价值。 《商业与经济统计杂志》，美国统计协会，第22卷，第367-381页。

Finance.yahoo.com. (2019). Yahoo Finance. [online] Available at: https://finance.yahoo.com/quote/KAZ.L?p=KAZ.L&.tsrc=fin-srch

Finance.yahoo.com。 (2019)。 雅虎财经。 [在线]可用： https : //finance.yahoo.com/quote/KAZ.L?p=KAZ.L&.tsrc=fin-srch

Glasserman, P., Heidelberger, P., and Shahabuddin, P. (2002). Portfolio value‐at‐ risk with heavy‐tailed risk factors. Mathematical Finance, 12(3), 239-269.

Glasserman，P.，Heidelberger，P.和Shahabuddin，P.(2002)。 具有重尾风险因素的投资组合风险值。 数学金融，12(3)，239-269。

Kazminerals.com. (2019). KAZ Minerals | About us. [online] Available at: https://www.kazminerals.com/about-us.

Kazminerals.com。 (2019)。 KAZ Minerals | 关于我们。 [在线]可在以下网址获得： https ： //www.kazminerals.com/about-us 。

Lechner, L. A., and Ovaert, T. C. (2010). Value-at-risk: Techniques to account for leptokurtosis and asymmetric behavior in returns distributions. The Journal of Risk Finance, 11(5), 464-480.

Lechner，LA和Ovaert，TC(2010)。 风险价值：在收益分配中解决瘦态和不对称行为的技术。 风险金融杂志，11(5)，464-480。

Linsmeier, T. J., and Pearson, N. D. (2000). Value at risk. Financial Analysts Journal, 56(2), 47-67. London Stock Exchange (2019). KAZ MINERALS share price (KAZ)… [online] Available at: https://www.londonstockexchange.com

Linsmeier，TJ和Pearson，ND(2000)。 价值风险。 金融分析师杂志，56(2)，47-67。 伦敦证券交易所(2019)。 KAZ MINERALS股票价格(KAZ)…[在线] 网址 ： https : //www.londonstockexchange.com

Phelps S. (2018). Estimating Value-At-Risk (VaR) in Python.7CCSMSCF Scientific Computing for Finance(18~19 SEM1 000001)

菲尔普斯(2018)。 用Python估算风险价值(VaR).7CCSMSCF金融科学计算(18〜19 SEM1 000001)

Rockafellar, R. T., and Uryasev, S. (2000). Optimization of conditional valueat-risk. Journal of risk, 2, 21-42.

Rockafellar，RT和Uryasev，S.(2000)。 条件风险价值的优化。 风险杂志，2，21-42。

Vee, D. N. C., and Gonpot, P. N. (2014). An application of extreme value theory as a risk measurement approach in frontier markets. World Academy of Science, Engineering and Technology, International Journal of Mathematical, Computational, Physical, Electrical and Computer Engineering, 8(6), 919-929.

Vee，DNC和Gonpot，PN(2014)。 极值理论在前沿市场中作为风险度量方法的应用。 世界科学，工程和技术研究院，《国际数学，计算，物理，电气和计算机工程杂志》 8(6)，919-929。

Zinouri, N. (2016). Improving healthcare resource management through demand prediction and staff scheduling (Order No. 10151957). (1815794760).Retrieved from https://search.proquest.com/docview/1815794760?accountid=11862

Zinouri，N.(2016年)。 通过需求预测和人员安排改善医疗资源管理(订单号10151957)。 (1815794760)。取自https://search.proquest.com/docview/1815794760?accountid=11862

翻译自: https://habr.com/en/post/447542/