金融市场：Open.Yale.course：Financial.Markets.07.Chi_Eng

 

期望效应理论

 

1959年， 有一天Gem和他的同事Gin在餐馆吃饭（他们俩都是大学教授），Gem是一位喜欢开玩笑的人，于是想和Gin做个游戏，游戏的规则是猜硬币正反（就一次），如果Gin猜对了，Gem愿意付200$给Gin，如果Gin猜错，Gin付100$给他，（那个年代的100$相当于现在的1000$，是一个不小的数目，但他们都能付的起），Gin不干（赌局虽对他有利）；于是Gem换一种方法玩，他们就猜100百次硬币的正反面，每次，如果Gin猜对了，Gem愿意付200$给Gin，如果Gin猜错，Gin付100$给他，（那个年代的100$相当于现在的1000$，Gin立马答应（他认为他的概率学的还不错）。不过这只不过是Gem一次玩笑而已。

 

根据二项式分布，Gin认为他肯定赢定了。上面的例子可以看出Gin在面对机遇的时候的非理性的行为，我们不能说Gin愿意接受100次这样的赌局，但我不愿意接受1次这样的赌局是不理性的。人类的效应函数上出现一个拐点。

 

A、下面两件事件中，你只能其中一种：

1、完成X1事件，你有25%概率获取3000￥

2、完成X2事件，你有20%概率获取4000￥

 

B、在另两件事件中，你也只能选择其中一种：

1、  完成X3事件，你有100%概率获取3000￥

2、  完成X4事件，你有80%概率获取4000￥

 

我相信大部分人都选择A(2)、B(1)

 

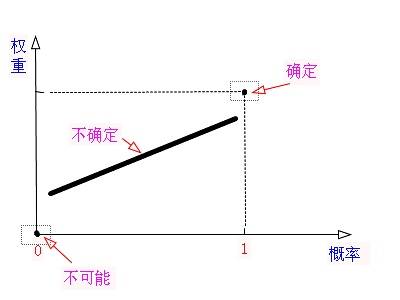
期望效应理论：不可能、不确定和确定这三种情况。上面的图就可以解释大部分人的选择的原因。

我最近在玩和讯微博，很方便，很实用，你也来和我一起玩吧！
去看看我的微博吧！http://t.hexun.com/3006897/default.html