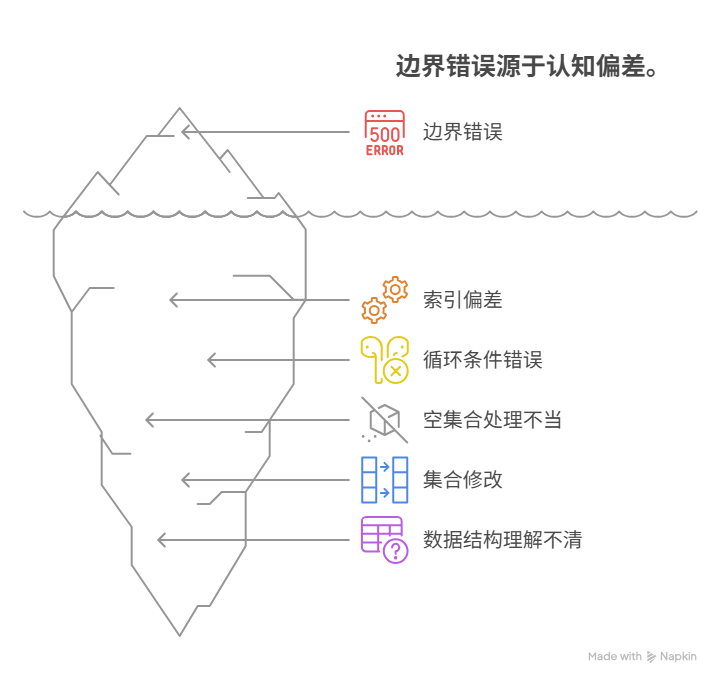
为什么操作集合的边界元素时，代码总会出错

最新推荐文章于 2025-12-04 16:02:12 发布

原创最新推荐文章于 2025-12-04 16:02:12 发布 · 900 阅读

CC 4.0 BY-SA版权

文章标签：

在程序中，对集合（如数组、列表）的边界元素进行操作时之所以总会出错，其核心原因在于程序员的“直觉计数”与计算机的“索引机制”之间，存在着一个根本性的、常常被忽略的“差一”认知偏差。这种偏差，会在处理循环和边界判断时，被急剧放大，从而引发一系列问题。导致边界错误的五大典型场景包括：源于计算机“从0开始”的索引机制与人类“从1开始”的计数直觉的冲突、循环的“终止条件”设置错误导致“差一”访问、对“空集合”这一特殊边界情况的处理不当、在迭代过程中修改集合导致边界“动态变化”、以及对不同数据结构（如数组与链表）的边界特性理解不清。

其中，循环的“终止条件”设置错误，是最直接的“罪魁祸首”。例如，一个长度为10的数组，其有效的索引范围是0到9。如果开发者在循环中，不假思索地，写下了i <= 10这样的判断条件，那么当循环进行到最后一次，i等于10时，程序就会试图去访问一个物理上不存在的、索引为10的内存空间，从而必然导致“数组越界”的致命错误。

一、问题的根源：直觉与逻辑的“时差”

在编程世界中，处理集合的边界，如同在悬崖边上行走，一步之差，便可能谬以千里。这类错误的频发，其根源，并非是逻辑本身有多么高深，而恰恰是它与我们的“日常直觉”发生了根本性的冲突。

1. “零基索引”：计算机世界的“第一铁律”

我们必须首先，将一个核心概念，内化为“肌肉记忆”：在几乎所有主流编程语言中，集合的索引，都是“从0开始”的。

一个包含N个元素的数组，其第一个元素的索引是0。

其最后一个元素的索引是N-1。

其“长度”是N，但其“最大合法索引”，永远是长度 - 1。

2. “长度”与“最大索引”的混淆：万恶之源

绝大多数的边界错误，都源于将集合的“长度”，与“最大索引”，这两个在数值上恰好“差一”的概念，进行了混淆。当我们试图去访问 myArray[myArray.length] 时，我们实际上，是在试图访问那个位于“最后一个元素”之后的、一个不存在的“幽灵”元素。

3. “栅栏柱问题”

这个经典的“差一”问题，在数学和计算机科学中，有一个专门的名字，叫做“栅栏柱问题”。

问题：要用10段栅栏，围成一条直线型的栅栏，你需要多少根栅栏柱？

直觉答案：10根？

正确答案：11根。因为每一段栅栏，都需要一根“结束”的柱子，而第一段栅栏，还需要一根“开始”的柱子。

在处理集合边界时，我们常常会陷入类似的逻辑陷阱。正如计算机科学先驱艾兹赫尔·戴克斯特拉所强调的，编程，是一项需要极致精确的智力活动。任何基于“想当然”的直觉，都可能在边界问题上，付出惨痛的代价。

二、“犯罪现场”一：对“最后一个”元素的误判

这是最常见的、也是最典型的边界错误“犯罪现场”。

1. 典型错误：“小于等于”的滥用

错误代码：Java// 一个包含3个元素的字符串数组 String[] names = {"张三", "李四", "王五"}; // 长度为3，最大索引为2 // 错误地，在循环终止条件中，使用了“小于等于” for (int i = 0; i <= names.length; i++) { System.out.println(names[i]); // 当i=3时，程序将崩溃 }

执行过程分析：

当i的值为0, 1, 2时，循环正常执行，分别打印出“张三”、“李四”、“王五”。

当i等于2的循环结束后，循环头部的i++被执行，i的值变为3。

此时，进行边界检查：i <= names.length，即 3 <= 3，该条件被判断为真。

循环，因此，多执行了一次。

在循环体内，程序试图去访问names[3]。然而，这个数组，最大的合法索引是2。

后果：程序因为试图访问一个不存在的内存地址，而被操作系统或运行时环境，强制中止，并抛出一个致命的“数组索引越界”异常。

2. “空集合”的特殊情况

对“最后一个”元素的处理，还必须警惕一个最特殊的边界——“空集合”。

错误代码：JavaList<String> userList = new ArrayList<>(); // 一个空的列表 // 在访问前，没有进行“判空”检查 String lastUser = userList.get(userList.size() - 1); // 此处将崩溃

问题分析：当userList为空时，userList.size()的值是0。那么，userList.size() - 1的结果就是-1。试图去访问一个列表的-1索引，同样是一种非法的“越界”行为。

【解决方案】：

黄金法则：在进行基于索引的正序遍历时，循环的终止条件，永远，都应使用“小于” (<)，而非“小于等于” (<=)。

防御性编程：在试图通过索引，来直接访问任何一个元素（特别是第一个或最后一个）之前，都必须，先对集合的“大小”或“是否为空”，进行一次前置的判断。

三、“犯罪现场”二：对“第一个”元素的处理

除了“终点”的悬崖，集合的“起点”，同样充满了陷阱。

1. 访问“前一个”元素的风险

场景：我们需要遍历一个价格列表，并计算出，每一天的价格，相比于“前一天”的变化量。

错误代码：Javadouble[] prices = {10.0, 10.5, 11.2}; for (int i = 0; i < prices.length; i++) { // 试图计算当前价格与“前一个”价格的差值 double diff = prices[i] - prices[i-1]; // 当i=0时，此处将崩溃 System.out.println("价格变化: " + diff); }

问题分析：这个循环的逻辑，在其内部，包含了对i-1索引的访问。当循环，进行到其第一次迭代，即i等于0时，i-1的结果是-1。程序，试图去访问prices[-1]，这同样，是一种致命的“数组索引越界”。

【解决方案】：当循环体内的逻辑，需要同时处理“当前项”和“前一项（或后一项）”时，我们必须有意识地，去调整循环的“起止范围”，并对真正的“边界元素”，进行单独的、例外的处理。

修正后的代码：Javadouble[] prices = {10.0, 10.5, 11.2}; // 循环，从第二个元素（索引为1）开始 for (int i = 1; i < prices.length; i++) { double diff = prices[i] - prices[i-1]; System.out.println("价格变化: " + diff); }

四、“犯罪现场”三：迭代中“边界”的动态变化

这是一个更高级、也更隐蔽的错误。即，在循环遍历一个集合的过程中，通过“添加”或“删除”元素的操作，动态地，改变了集合自身的“边界”（即其大小）。

1. 删除元素导致“终点”提前，引发“跳过”

问题描述：如我们在前文《为什么在循环中修改集合，会导致程序出错》中所详述的，当你在一个正序的、基于索引的循环中，删除了一个元素时，列表的后续所有元素，都会向前“塌陷”一位。而你的循环计数器i，却依然会“照常”地+1。这一“进”一“退”，就导致了，那个刚刚“塌陷”过来的、新的位于索引i的元素，被**完美地“跳过”**了检查。

2. 添加元素导致“终点”远去，引发“无限循环”

问题描述：如果，你在一个基于i < list.size()为条件的循环中，持续地，向列表的尾部，添加新的元素，那么，list.size()这个“终点线”，就会被持续地，向“未来”推移。循环的计数器i，可能永远也追不上这条移动的“终点线”，从而，导致程序，陷入“无限循环”。

【解决方案】： 严禁，在循环遍历的过程中，直接地，修改被遍历的那个集合的大小。最安全、最推荐的“黄金范式”，是“先收集，后处理”。

第一遍循环（只读）：在第一遍循环中，我们只进行“读取”和“判断”操作，并将所有需要被“删除”或“添加”的元素，都分别地，放入到几个临时的“待处理”集合中。

循环后（写入）：在第一遍循环完全结束后，我们再对原始的集合，进行一次性的、批量的“添加”或“删除”操作。