
研究生复试已经开始,今年由于疫情原因大部分院校采用网上复试的方式。
网上复试对于现场复试还是有一些缺点,比如会受到到环境,网络的影响,所以一些院校对网上复试有一些特殊要求,比如要求素颜出镜,不得使用耳机,不得录音录屏,需要穿衣镜,1分钟不接电话视为放弃等等。
你遇到这样“个性”的要求了吗?我们来看看都有哪些院校提了“特殊要求”吧!
断网情况处理
东南大学
复试过程中,若发生考生方断网情况,复试小组工作人员将在第一时间电话联络考生,继续复试问答,请在电话铃响1分钟之内接听,如超时,作自动放弃本次复试处理。

南京大学
复试过程中若发生考生方断网情况,复试小组工作人员将在第一时间电话联络考生,继续复试问答,请在电话铃响1分钟之内接听,如超时,作自动放弃本次复试处理。如果院系有其他规定,以院系规定为准。

湖北中医药大学
复试过程中若考生方发生断网情况,复试小组工作人员将在第一时间电话(考生在研招网报名时预留手机号)联络考生,继续复试问答,请在电话铃响1分钟之内接听,如超时,作自动放弃本次复试处理。如果招生学院有其他规定,以学院规定为准。

西安建筑科技大学
复试过程中若发生考生方断网情况,面试小组工作人员将在第一时间电话联络考生,继续复试问答,请在电话铃响第一时间接听,如超过1分钟未接听,按自动放弃本次复试处理。如果学院有其他规定,以学院规定为准。

宝鸡文理学院
复试过程中若发生考生方断网情况,复试小组工作人员将在第一时间电话联络考生,继续复试问答,请在电话铃响1分钟之内接听,如超时,作自动放弃本次复试处理。如果学院有其他规定,以学院规定为准。

华北理工大学
如果网络在3分钟内能够及时恢复的,考试继续进行,但需变更考试题目;考生端网络超过3分钟不能及时恢复的,可安排该考生延后或改期复试,并开始下一位考生复试。

中国政治青年学院
在复试资格审核阶段和复试专业课面试,以及英语听、说测试阶段,如因通讯及设备故障等原因,经复试工作人员对考生连续进行三次呼叫,考生仍无应答,则继续与下一名考生联系。对于经三次呼叫未能取得联系的考生,交由研究生部工作人员继续联系,并查明情况、详细记录,视具体情况予以处理。对于在复试专业课面试,以及英语听、说测试阶段,如因通讯及设备故障等原因导致“微信视频”过程突然中断,由复试小组视具体情况进行处理,但原则上应当重新更换题目令考生作答,并适当延长考试时间。

复试特殊要求
北京城市学院
考生背后最好有立式穿衣镜,可看到考生对面环境。

四川大学电气工程学院
面试时考生本人应保持发型整洁,素颜、露耳、束发、不可佩戴口罩、不可佩戴首饰,不可穿带有拉链的衣服,面试不得使用耳机。

浙江理工大学
复试过程不得戴耳机,不得用头发或其他饰品遮挡耳部。复试过程中不得使用美颜及滤镜,本人全程出镜,不得中途离开座位,无关人员不得在考试区域内出现,否则视为违纪。

南开大学
90元每人,并且要求在5月8日前就要完成缴费,逾期不缴费则视为主动放弃复试!

浙江传媒学院
保证在考试过程中诚实守信,不违纪、不作弊、不协助作弊,复试全程只允许考生一人在面试房间;禁止将复试题目、面试过程等信息泄露给其他人员及私自录音、录像、录屏,如有违反,视同作弊。 复试全程进行实时人脸识别,考生不得化妆、戴美瞳、开美颜滤镜,不得戴帽子、口罩、墨镜等,头发捋至耳后。复试中考生不得东张西望,不得离开摄像范围或中途离场。

北京科技大学
复试期间考生不得录屏录像录音。

北京大学药学院
不允许采用任何方式变声、更改人像。

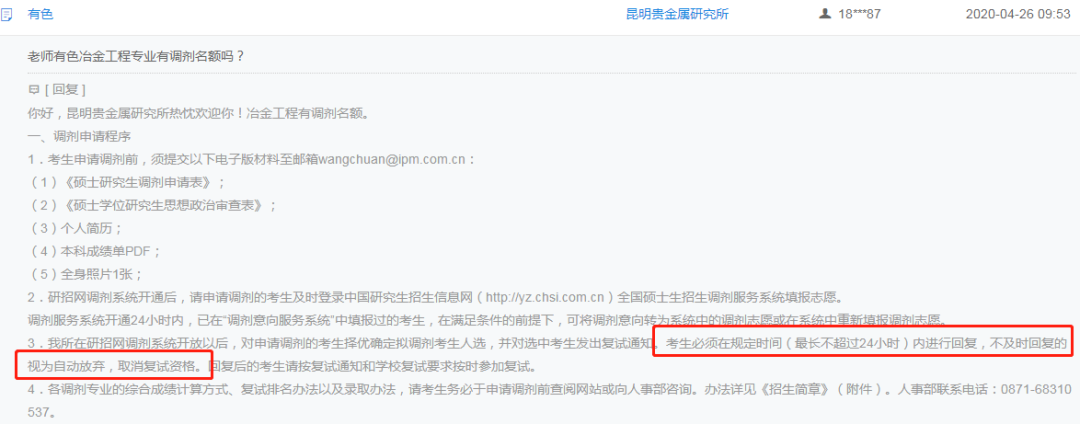
昆明贵金属研究所
对调剂的同学提了要求,如果没有在24小时之内回复,则视为放弃复试!
中国人民大学
信息学院、历史学院等学院发布了对于机位的要求,第二机位强调必须是可移动的。

武汉理工大学
要求双机位的主机位和辅机位都得用手机,并且规定了上传、下载网速应稳定在5Mbps以上。

中央财经大学
要求每人不少于3000字的个人自传。

四川大学
原子核科学技术研究所要求每人时长为5分钟的个人自述PPT汇报。

材料科学与工程学院公开要求上交不少于1000字的个人综述,包括自我评价、专业志趣、专业、职业规划等内容;还要有个人陈述5分钟左右的PPT,有木有感到亚历山大啊!

武汉大学
水利水电学院:5月12日-13日进行网络远程复试,使用腾讯会议、钉钉会议。
要求考生在5月8日前邮寄复试材料纸质版(包括大学成绩单、毕业设计报告(论文)全文或者主要成果摘要、获得的科技奖励和成果(发表论文)等)
厦门大学
2020年硕士研究生复试工作将集中在5月内启动,采用网络远程复试的形式,复试设备首选电脑,iPad或者手机备用。
推荐使用内置摄像头和麦克风的笔记本电脑或者带声卡的台式电脑外接摄像头和音箱。

PS:要求使用“随会”软件作为2020年硕士研究生复试软件。
厦大计划使用的“随会”复试软件,能量姐还是第一次听说,小伙伴们有使用过吗?如果没有使用过的,记得早点下载试用哦~
希望小伙伴们都能复试成功,顺利上岸,加油!
来源于网络
20调剂QQ群,每天公布最新的计算机/软件工程 调剂信息,欢迎加入
群号是 693487472





您还可以在以下平台找到我们

你点的每个在看,我都认真当成了喜欢























 4603
4603

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








