【案例共创】线性回归 - 汽车行驶里程与油耗关系预测

本案例由梅科尔工作室提供

1 概述

1.1 背景介绍

在机器学习领域，线性回归就是使用一个线性函数（多项式回归可以是曲线）去拟合给定的训练集，测试时，对输入的x值，返回这个线性函数的y值。最终目标是找到y=Θ0 + Θ1x1 + Θ2x2 + …… + Θnxn 函数式中的Θ0、Θ1、Θ2、……、Θn值。

通过本案例可以对线性回归进行学习，同时了解MindSpore框架的使用。

1.2 适用对象

• 企业
• 个人开发者
• 高校学生

1.3 案例时间

本案例总时长预计30分钟。

1.4 案例流程

说明：

① 登录开发者空间，启动Notebook； ② 在Notebook中编写代码运行调试。

1.5 资源总览

本案例预计花费总计0元。

资源名称	规格	单价（元）	时长（分钟）
开发者空间—Notebook	NPU basic · 1 * NPU 910B · 8v CPU · 24GB euler2.9-py310-torch2.1.0-cann8.0-openmind0.9.1-notebook	免费	30

2 资源与开发环境准备

2.1 启动Notebook

参考“DeepSeek模型API调用及参数调试（开发者空间Notebook版）”案例的第2.2章节启动Notebook。

2.2 安装依赖库

在Notebook的新执行框中输入如下代码并运行，安装所有依赖库。

!pip install numpy
!pip install mindspore
!pip install pandas 
!pip install matplotlib

3 汽车行驶里程与油耗关系预测

1. 导入必要的库

• numpy (np)：用于数值计算。
• mindspore：用于构建和训练神经网络。
• 张量操作：提供张量数据结构和相关的操作。
• 神经网络构建：用于定义模型、损失函数和优化器。
• 自动微分：自动计算梯度，用于模型的训练。
• 数据转换：将numpy数组转换为Tensor，以便在mindspore框架中进行计算。
• 模型输入和输出：作为模型的输入和输出数据类型。

在Notebook的新执行框中输入如下代码并运行，导入所有使用到的库。

import logging
import warnings
logging.disable(logging.CRITICAL)
warnings.filterwarnings("ignore")
import numpy as np
import mindspore as ms
from mindspore import nn, Tensor, context, Parameter, ops
import pandas as pd
import matplotlib.pyplot as plt

context.set_context(device_target="Ascend")

如提示兼容性警告可忽略，不影响模型训练和推理的正常运行。

2. 数据加载与预处理

数据准备：将如下链接数据集下载，并通过notebook上传。

https://dtse-mirrors.obs.cn-north-4.myhuaweicloud.com/case/0038/auto-mpg.data 下载到本地的数据 选中下载的数据集，拖拽到/目录进行上传。

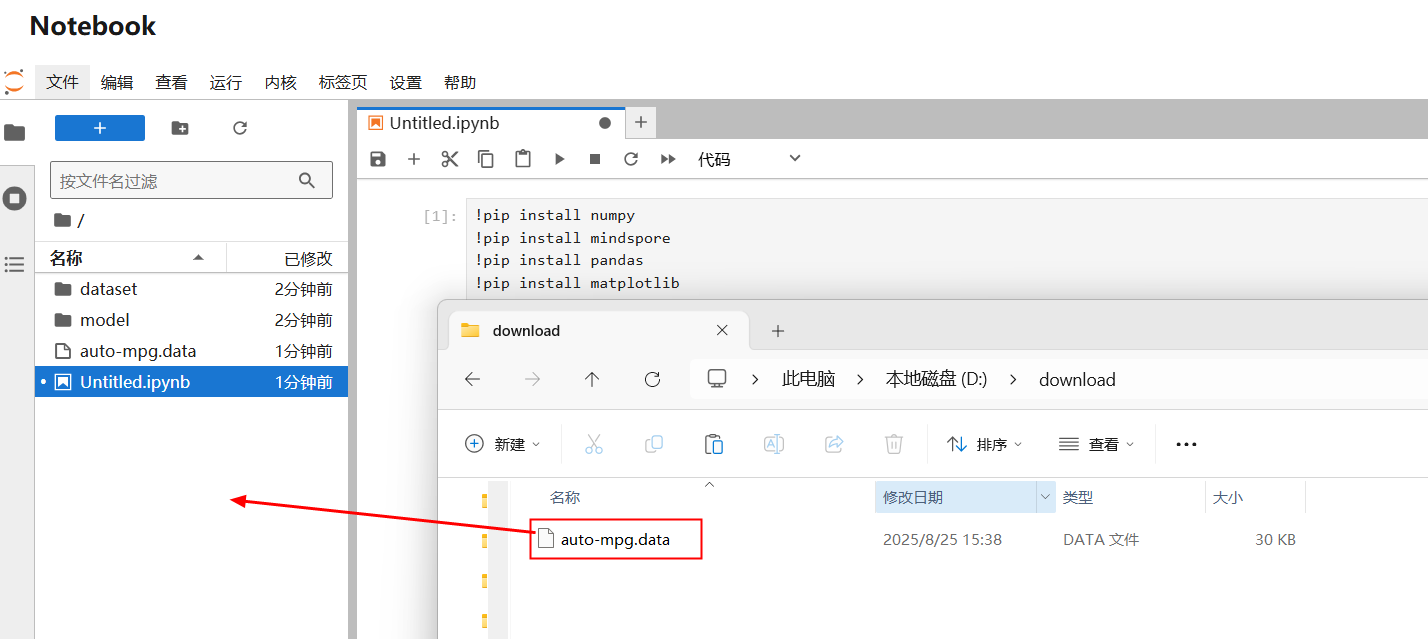
在Notebook的新执行框中输入如下代码并运行：

# 数据加载与预处理
path = 'auto-mpg.data'
columns = ["mpg", "cylinders", "displacement", "horsepower", "weight",
           "acceleration", "model year", "origin", "car name"]
try:
    cars = pd.read_csv(path, sep='\s+', names=columns)
except FileNotFoundError:
    print(f"错误：找不到文件 '{path}'")
    print("请确保文件位于当前工作目录，或提供正确的文件路径")
    exit()

# 数据预处理
cars = cars[cars.horsepower != '?']
cars['horsepower'] = cars['horsepower'].astype(float)

数据准备：

▪ 这段代码使用pandas 加载汽车数据集，并对数据进行初步处理。由于数据中的“horsepower”列包含字符串“?”，代码过滤掉这些行，并将“horsepower”列转换为浮点数类型。这一步是必要的，因为机器学习模型需要数值型数据进行训练。

3. 数据划分与标准化 数据标准化：对特征和目标变量进行标准化（均值为0，方差为1），加速模型收敛。 标准化空间：模型在标准化后的数据上训练，最终通过反标准化将参数转换回原始尺度。

在Notebook的新执行框中输入如下代码并运行：

# 数据划分
# 准备数据
Y = cars['mpg'].values
X = cars[['weight']].values

# 划分数据集
from sklearn.model_selection import train_test_split
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=0.2, random_state=0)

# 打印数据形状进行验证
print(f"训练集: X_train={X_train.shape}, Y_train={Y_train.shape}")
print(f"测试集: X_test={X_test.shape}, Y_test={Y_test.shape}")

from sklearn.preprocessing import StandardScaler

# 对特征进行标准化
scaler_X = StandardScaler()
X_train_scaled = scaler_X.fit_transform(X_train)
X_test_scaled = scaler_X.transform(X_test)

# 对目标变量进行标准化
scaler_Y = StandardScaler()
Y_train_scaled = scaler_Y.fit_transform(Y_train.reshape(-1, 1)).flatten()
Y_test_scaled = scaler_Y.transform(Y_test.reshape(-1, 1)).flatten()

# 转换为列向量
Y_train_scaled = Y_train_scaled.reshape(-1, 1)

# 转换为 MindSpore 张量
X_train_ms = Tensor(X_train_scaled, dtype=ms.float32)
Y_train_ms = Tensor(Y_train_scaled, dtype=ms.float32)
X_test_ms = Tensor(X_test_scaled, dtype=ms.float32)
Y_test_ms = Tensor(Y_test_scaled.reshape(-1, 1), dtype=ms.float32)

4. 模型定义与训练

自定义模型：通过继承nn.Cell定义线性回归模型，支持自定义权重初始化。 分批次训练：将数据划分为小批量（batch size=32），减少内存占用并加速训练。 学习率调整：标准化后数据尺度统一，可使用稍大的学习率（0.01）。

在Notebook的新执行框中输入如下代码并运行：

class LinearRegression(nn.Cell):
    def __init__(self):
        super(LinearRegression, self).__init__()
        # 初始化权重和偏置
        self.weight = Parameter(Tensor(np.random.randn(1, 1).astype(np.float32) * 0.01), name="weight")
        self.bias = Parameter(Tensor(np.array([0.0]).astype(np.float32)), name="bias")

    def construct(self, x):
        # 确保x是二维的
        if len(x.shape) == 1:
            x = ops.expand_dims(x, 1)

        # 线性变换: y = wx + b
        output = ops.matmul(x, self.weight)
        output = output + self.bias
        return output

# 初始化模型
model = LinearRegression()

# 损失函数: 均方误差 (MSE)
loss_fn = nn.MSELoss()

# 修复3: 使用更合理的学习率（标准化后可以使用稍大的学习率）
learning_rate = 0.01  # 标准化后可以使用更大的学习率
optimizer = nn.SGD(model.trainable_params(), learning_rate=learning_rate)

# 修复4: 简化训练步骤，使用标准TrainOneStepCell
class WithLossCell(nn.Cell):
    def __init__(self, backbone, loss_fn):
        super(WithLossCell, self).__init__(auto_prefix=False)
        self._backbone = backbone
        self._loss_fn = loss_fn

    def construct(self, data, label):
        prediction = self._backbone(data)
        return self._loss_fn(prediction, label)

# 创建训练网络
train_net = nn.TrainOneStepCell(
    network=WithLossCell(model, loss_fn),
    optimizer=optimizer
)

epochs = 100
train_losses = []

print("\n开始训练...")
for epoch in range(epochs):
    total_loss = 0
    step = 0

    # 创建小批量
    batch_size = 32
    num_batches = len(X_train_scaled) // batch_size + (1 if len(X_train_scaled) % batch_size != 0 else 0)

    for i in range(num_batches):
        start_idx = i * batch_size
        end_idx = min((i + 1) * batch_size, len(X_train_scaled))

        # 获取当前批次
        feature_batch = X_train_scaled[start_idx:end_idx]
        label_batch = Y_train_scaled[start_idx:end_idx]

        # 转换为张量
        feature = Tensor(feature_batch, ms.float32)
        label = Tensor(label_batch, ms.float32)

        # 执行单步训练
        loss = train_net(feature, label)
        total_loss += float(loss.asnumpy())
        step += 1

    # 计算平均损失
    avg_loss = total_loss / max(1, step)
    train_losses.append(avg_loss)

    # 打印训练进度
    if (epoch + 1) % 10 == 0 or epoch == 0:
        print(f"Epoch [{epoch+1:3d}/{epochs}], Loss: {avg_loss:.6f}")

如遇信息性警告，不会影响模型训练和推理的正常运行。

5. 参数反标准化与模型评估

参数反标准化：将标准化空间中的权重和偏置转换回原始尺度，公式推导如下： R²分数：手动计算决定系数（R²），评估模型拟合优度。

在Notebook的新执行框中输入如下代码并运行：

weight_scaled = model.weight.asnumpy()[0, 0]
bias_scaled = model.bias.asnumpy()[0]

# 将参数转换回原始尺度
# y_scaled = weight_scaled * x_scaled + bias_scaled
# (y - mean_y) / std_y = weight_scaled * (x - mean_x) / std_x + bias_scaled
# y = (weight_scaled * std_y / std_x) * x + (mean_y - weight_scaled * std_y * mean_x / std_x + bias_scaled * std_y)
weight = weight_scaled * (scaler_Y.scale_[0] / scaler_X.scale_[0])
bias = scaler_Y.mean_[0] - weight_scaled * scaler_Y.scale_[0] * scaler_X.mean_[0] / scaler_X.scale_[0] + bias_scaled * scaler_Y.scale_[0]

print(f"\nMindSpore 训练结果 (原始尺度):")
print(f"Weight (斜率): {weight:.6f}")
print(f"Bias (截距): {bias:.6f}")

# 使用原始尺度的预测值
def predict_original_scale(x_scaled):
    """将标准化输入转换为原始尺度的预测值"""
    x = scaler_X.inverse_transform(x_scaled.reshape(-1, 1)).flatten()
    y_scaled = model(Tensor(x_scaled, ms.float32)).asnumpy().flatten()
    y = scaler_Y.inverse_transform(y_scaled.reshape(-1, 1)).flatten()
    return y

# 预测测试集（在原始尺度上）
predictions = predict_original_scale(X_test_scaled)

# 手动计算 R² 分数
def r2_score(y_true, y_pred):
    ss_res = np.sum((y_true - y_pred) ** 2)
    ss_tot = np.sum((y_true - np.mean(y_true)) ** 2)
    return 1 - (ss_res / ss_tot)

r2 = r2_score(Y_test, predictions)
print(f"R² Score: {r2:.4f}")

6. 可视化与对比

训练损失曲线：使用对数刻度展示损失下降趋势，直观反映模型收敛速度。 模型对比：通过scikit-learn实现相同任务，验证MindSpore模型的正确性。 在Notebook的新执行框中输入如下代码并运行：

# 绘制训练损失曲线
plt.figure(figsize=(14, 10))

plt.subplot(2, 2, 1)
plt.plot(train_losses)
plt.title('Training Loss Curve')
plt.xlabel('Epochs')
plt.ylabel('MSE Loss')
plt.grid(True)
plt.yscale('log')  # 使用对数刻度更清晰地显示损失下降

# 绘制训练数据与预测结果
plt.subplot(2, 2, 2)
plt.scatter(X_train, Y_train, color='red', alpha=0.3, label='Train Data')
# 生成预测线
x_range = np.linspace(X_train.min(), X_train.max(), 100)
x_range_scaled = scaler_X.transform(x_range.reshape(-1, 1)).flatten()
y_pred = predict_original_scale(x_range_scaled)
plt.plot(x_range, y_pred, color='green', linewidth=2, 
         label=f'Prediction: y={weight:.4f}x + {bias:.4f}')
plt.scatter(X_train, predict_original_scale(scaler_X.transform(X_train)), 
            color='green', alpha=0.3, label='Train Predictions')
plt.xlabel('Weight (lbs)')
plt.ylabel('MPG')
plt.title('Train Data vs Predictions')
plt.legend()
plt.grid(True)

# 绘制测试数据与预测结果
plt.subplot(2, 2, 3)
plt.scatter(X_test, Y_test, color='blue', alpha=0.3, label='Test Data')
plt.plot(x_range, y_pred, color='green', linewidth=2, 
         label=f'Prediction: y={weight:.4f}x + {bias:.4f}')
plt.scatter(X_test, predictions, color='green', alpha=0.3, label='Test Predictions')
plt.xlabel('Weight (lbs)')
plt.ylabel('MPG')
plt.title(f'Test Data vs Predictions (R²={r2:.4f})')
plt.legend()
plt.grid(True)

运行结果：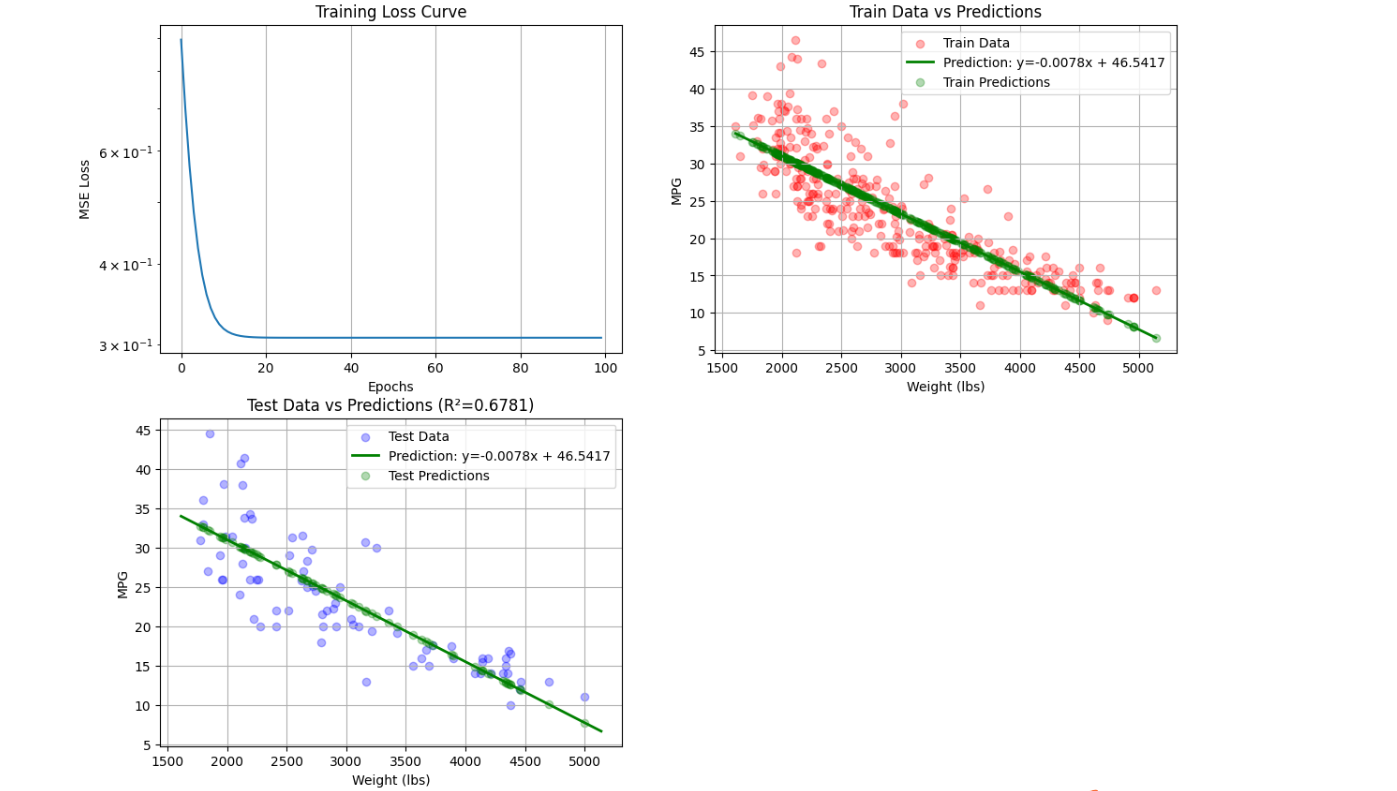

7. 计算黑塞矩阵

黑塞矩阵计算：将 X_train 转换为包含偏置项的 numpy 数组，然后计算其转置与⾃⾝的点积，得到黑塞矩阵。

在Notebook的新执行框中输入如下代码并运行：

# 对于线性回归，黑塞矩阵 = X^T * X
# 添加偏置项 (1) 到特征矩阵
X_matrix = np.hstack((X_train_scaled, np.ones((X_train_scaled.shape[0], 1))))
# 转换为 MindSpore 张量
X_tensor = Tensor(X_matrix, dtype=ms.float32)

# 计算 X^T * X
hessian = ops.matmul(ops.transpose(X_tensor, (1, 0)), X_tensor).asnumpy()

print(f"\n黑塞矩阵 (标准化空间):\n{hessian}")

# 可视化黑塞矩阵
plt.subplot(2, 2, 4)
plt.imshow(hessian, cmap='viridis')
plt.colorbar()
plt.title('Hessian Matrix')
plt.xticks([0, 1], ['weight', 'bias'])
plt.yticks([0, 1], ['weight', 'bias'])
for i in range(2):
    for j in range(2):
        plt.text(j, i, f'{hessian[i, j]:.2f}', 
                 ha="center", va="center", color="w")
plt.tight_layout()
plt.savefig('mindspore_regression_results.png', dpi=300, bbox_inches='tight')
plt.show()

try:
    from sklearn.linear_model import LinearRegression
    lr = LinearRegression()
    lr.fit(X_train, Y_train)

    print("\nscikit-learn 结果对比:")
    print(f"Weight (斜率): {lr.coef_[0]:.6f}")
    print(f"Bias (截距): {lr.intercept_:.6f}")
    print(f"R² Score: {lr.score(X_test, Y_test):.4f}")

    # 添加对比到可视化
    plt.figure(figsize=(10, 6))
    plt.scatter(X_test, Y_test, color='blue', alpha=0.5, label='Test Data')
    plt.plot(x_range, y_pred, 'g-', 
             label=f'MindSpore: y={weight:.4f}x + {bias:.4f}')
    plt.plot(x_range, lr.coef_[0] * x_range + lr.intercept_, 'r--', 
             label=f'scikit-learn: y={lr.coef_[0]:.4f}x + {lr.intercept_:.4f}')
    plt.xlabel('Weight (lbs)')
    plt.ylabel('MPG')
    plt.title('Model Comparison: MindSpore vs scikit-learn')
    plt.legend()
    plt.grid(True)
    plt.savefig('model_comparison.png', dpi=300, bbox_inches='tight')
    plt.show()

except ImportError:
    print("\n注意: 未安装 scikit-learn，无法进行结果对比")

4 总结

根据上述训练预测结果，总结如下：

1. 模型参数

• 训练完成后，模型会输出两个参数：Bias（偏置项）和Weight（里程数的权重）。

2. 可视化

• 可视化预测结果。

3. 黑塞矩阵

• 计算了黑塞矩阵，用于衡量损失函数在参数空间中的曲率，反映了模型参数的敏感性和优化的稳定性。