【数组与链表】循环链表实战 - 约瑟夫问题求解

一、概述

1. 案例介绍

循环链表是线性链表的一种重要变体。其核心特征在于打破了传统链表的线性结构，将链表的“最后一个节点”不再指向空 (NULL)，而是重新指向链表的“第一个节点”，从而形成一个闭合的环状结构。约瑟夫问题是一个经典的数学问题：n个人围成一圈，从第1个人开始报数，数到m的人出列，然后从下一个人重新开始报数，数到m的人再出列，如此循环，直到所有人出列为止。要求输出出列顺序。 该案例直观展示了循环链表在解决环形数据淘汰问题中的高效性和简洁性，是数据结构与算法结合的经典实战。 本案例相关实验将在华为云开发者空间云主机进行，开发者空间云主机为开发者提供了高效稳定的云资源，确保用户的数据安全。云主机当前已适配完整的C/C++开发环境，支持VS Code等多种IDE工具安装调测。

2. 适用对象

• 个人开发者
• 高校学生

3. 案例时间

本案例总时长预计40分钟。

4. 案例流程

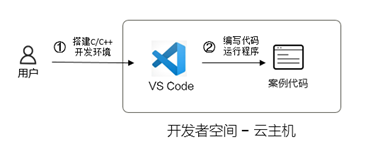
说明：

1. 开通开发者空间，搭建C/C++开发环境；
2. 打开VS Code，编写代码运行程序。

5. 资源总览

本案例预计花费0元。

资源名称	规格	单价（元）	时长（分钟）
华为开发者空间 - 云主机	鲲鹏通用计算增强型 kc2.xlarge.2 | 4vCPUs8G | Ubuntu	免费	40
VS Code	1.97.2	免费	40

二、配置实验环境

1. 开发者空间配置

面向广大开发者群体，华为开发者空间提供一个随时访问的“开发桌面云主机”、丰富的“预配置工具集合”和灵活使用的“场景化资源池”，开发者开箱即用，快速体验华为根技术和资源。

如果还没有领取开发者空间云主机，可以参考免费领取云主机文档领取。

领取云主机后可以直接进入华为开发者空间工作台界面，点击打开云主机 > 进入桌面连接云主机。

2. 配置实验环境

参考案例中心《基于开发者空间，定制C&C++开发环境云主机镜像》“2. 实验环境搭建”、“3. VS Code安装部署”章节完成开发环境、VS Code及插件安装。

三、循环链表实战：约瑟夫问题求解

1. 循环链表定义、结构及特点

循环链表 (Circular Linked List) 是线性链表的一种重要变体。其核心特征在于打破了传统链表的线性结构，将链表的“最后一个节点”不再指向空 (NULL)，而是重新指向链表的“第一个节点”，从而形成一个闭合的环状结构。

核心结构与特点： - 环形连接：这是循环链表最根本的特性。尾节点的 next 指针指向头节点（或头节点之前的有效节点），而不是 NULL。 - 无明确终点：由于首尾相连，链表没有传统意义上的“开始”或“结束”节点。可以从任意节点出发遍历整个链表。 - 头指针/头节点： 带空头节点： 常见做法是使用一个不存储实际数据的“头节点”(Dummy Node)。头节点的 next 指向第一个实际数据节点，最后一个实际数据节点的 next 指回头节点本身。这简化了空链表判断和插入/删除操作。 直接头指针： 也可以只有一个指向第一个实际数据节点的指针。此时，最后一个节点的 next 指向第一个节点。空链表时该指针为 NULL。 - 类型： 单向循环链表： 每个节点只包含数据域 (data) 和一个指向后继节点 (next) 的指针。尾节点的 next 指向头节点（或头节点）。 双向循环链表： 每个节点包含数据域 (data)、指向后继节点 (next) 的指针和指向前驱节点 (prev) 的指针。头节点的 prev 指向尾节点，尾节点的 next 指向头节点。这提供了双向遍历的能力。

2. 约瑟夫问题描述及求解步骤

问题描述：

约瑟夫问题是一个经典的数学问题：n个人围成一圈，从第1个人开始报数，数到m的人出列，然后从下一个人重新开始报数，数到m的人再出列，如此循环，直到所有人出列为止。要求输出出列顺序。

约瑟夫问题求解步骤：

(1) 数据结构定义

typedef struct Node {
    int data;           // 存储人员编号
    struct Node* next;  // 指向下一个节点的指针
} Node;

定义了一个简单的链表节点结构，每个节点包含： - data：存储人员的编号（1到n）； - next：指向下一个节点的指针。

(2) 创建循环链表

Node* createCircularList(int n) {
    Node *head = NULL;   // 链表头指针
    Node *prev = NULL;   // 前一个节点指针

    for (int i = 1; i <= n; i++) {
        // 创建新节点
        Node* newNode = (Node*)malloc(sizeof(Node));
        newNode->data = i;
        newNode->next = NULL;

        // 处理链表连接
        if (head == NULL) {
            head = newNode;
        } else {
            prev->next = newNode;
        }
        prev = newNode;
    }

    // 形成循环链表
    if (prev != NULL) {
        prev->next = head;
    }

    return head;
}

这个函数创建了一个包含n个节点的循环链表： - 循环创建n个节点，每个节点存储一个人的编号； - 将节点连接成单向链表； - 最后将尾节点的next指向头节点，形成循环链表。

(3) 约瑟夫问题求解

void josephus(int n, int m) {
    // 创建循环链表
    Node* head = createCircularList(n);
    Node* current = head;    // 当前节点指针
    Node* prev = NULL;       // 前驱节点指针
    int remaining = n;       // 剩余人数
    while (remaining > 1) {
        // 找到第m个节点
        for (int count = 1; count < m; count++) {
            prev = current;
            current = current->next;
        }
        // 删除当前节点（出列）
        Node* toDelete = current;

        // 调整链表连接
        if (prev != NULL) {
            prev->next = current->next;
        }

        // 移动到下一个节点
        current = current->next;

        // 特殊处理：如果删除的是头节点
        if (toDelete == head) {
            head = head->next;
        }

        // 释放内存并更新剩余人数
        free(toDelete);
        remaining--;
    }
    // 处理最后一个节点
    printf("最后留下的人员：%d\n", head->data);
    free(head);
}

求解过程分为5个关键步骤： - 创建循环链表：表示n个人围成的圈； - 初始化指针： current：指向当前报数的人； prev：指向当前节点的前一个节点（用于删除操作）。 - 找到第m个节点： 从当前节点开始，移动m-1次； 此时current指向的就是要出列的人。 - 删除节点： 调整链表连接，跳过当前节点； 释放被删除节点的内存； 更新剩余人数。 - 处理最后一个节点：当只剩一个人时，输出结果并释放内存。

(4) 可视化输出 代码中添加了详细的输出信息，帮助理解求解过程：

printf("当前从 %d 开始报数：", current->data);
for (int count = 1; count < m; count++) {
    prev = current;
    current = current->next;
    printf("%d ", current->data);
}
printf("\n→ 报数到 %d，出列人员：%d\n", m, toDelete->data);
printf("剩余人员圈：");
displayList(head, remaining);

这段代码在每次报数和出列时打印： - 当前报数过程； - 出列的人员编号； - 剩余人员组成的圈。

3. 完整代码实现及示例运行

完整代码实现： Step1：复制以下代码，替换main.cpp文件中的代码。

#include <stdio.h>
#include <stdlib.h>

// 定义链表节点结构
typedef struct Node {
    int data;           // 存储人员编号
    struct Node* next;  // 指向下一个节点的指针
} Node;

// 函数声明
Node* createCircularList(int n);
void displayList(Node* head, int n);
void josephus(int n, int m);

int main() {
    int n, m;

    printf("============= 约瑟夫问题求解器 =============\n");
    printf("问题描述：n个人围成一圈，从1开始报数，数到m的人出列\n");
    printf("然后从下一个人重新开始报数，直到所有人出列\n\n");

    printf("请输入总人数n：");
    scanf("%d", &n);
    printf("请输入报数上限m：");
    scanf("%d", &m);

    if (n <= 0 || m <= 0) {
        printf("\n错误：输入必须为正整数！\n");
        return 1;
    }

    josephus(n, m);
    return 0;
}

// 创建包含n个节点的循环链表
Node* createCircularList(int n) {
    Node *head = NULL;   // 链表头指针
    Node *prev = NULL;   // 前一个节点指针

    // 循环创建n个节点
    for (int i = 1; i <= n; i++) {
        // 分配新节点内存
        Node* newNode = (Node*)malloc(sizeof(Node));
        if (newNode == NULL) {
            printf("内存分配失败！\n");
            exit(1);
        }

        // 初始化新节点
        newNode->data = i;
        newNode->next = NULL;

        // 如果是第一个节点，设置为头节点
        if (head == NULL) {
            head = newNode;
        } else {
            // 否则将前一个节点的next指向新节点
            prev->next = newNode;
        }

        // 更新prev指针为新节点
        prev = newNode;
    }

    // 将最后一个节点的next指向头节点，形成循环链表
    if (prev != NULL) {
        prev->next = head;
    }

    return head;
}

// 显示循环链表
void displayList(Node* head, int n) {
    if (head == NULL) {
        printf("链表为空！\n");
        return;
    }

    printf("当前人员圈：");
    Node* temp = head;
    for (int i = 0; i < n; i++) {
        printf("%d", temp->data);
        if (i < n - 1) {
            printf(" → ");
        }
        temp = temp->next;
    }
    printf("\n");
}

// 解决约瑟夫问题
void josephus(int n, int m) {
    printf("\n===== 开始求解约瑟夫问题(n=%d, m=%d) =====\n", n, m);

    // 1. 创建循环链表
    Node* head = createCircularList(n);
    printf("初始人员圈创建完成：");
    displayList(head, n);

    Node* current = head;    // 当前节点指针
    Node* prev = NULL;       // 前驱节点指针
    int remaining = n;       // 剩余人数

    printf("\n开始报数过程...\n");

    // 2. 遍历直到只剩一个节点
    while (remaining > 1) {
        // 3. 找到第m个节点
        printf("\n当前从 %d 开始报数：", current->data);
        for (int count = 1; count < m; count++) {
            prev = current;
            current = current->next;
            printf("%d ", current->data);
        }

        // 4. 删除当前节点（出列）
        Node* toDelete = current; // 要删除的节点

        // 特殊情况处理：当要删除的是头节点时
        if (toDelete == head) {
            head = head->next;
        }

        printf("\n→ 报数到 %d，出列人员：%d\n", m, toDelete->data);

        // 调整链表连接
        if (prev != NULL) {
            prev->next = current->next;
        }

        // 移动到下一个节点
        current = current->next;

        // 释放被删除节点的内存
        free(toDelete);
        remaining--; // 剩余人数减1

        // 显示当前剩余人员
        printf("剩余人员圈：");
        displayList(head, remaining);
    }

    // 5. 处理最后一个节点
    printf("\n===== 最终结果 =====\n");
    printf("最后留下的人员：%d\n", head->data);
    free(head); // 释放最后一个节点的内存

    printf("问题求解完成！\n");
}

Step2：点击编辑器左上角运行按钮直接运行。

Step3：输入n=5，按下Enter键，输入m=3，按下Enter键，控制台输出内容。

输出内容截图：

输出内容文本显示：

============= 约瑟夫问题求解器 =============
问题描述：n个人围成一圈，从1开始报数，数到m的人出列
然后从下一个人重新开始报数，直到所有人出列

请输入总人数n：5
请输入报数上限m：3

===== 开始求解约瑟夫问题(n=5, m=3) =====
初始人员圈创建完成：当前人员圈：1 → 2 → 3 → 4 → 5

开始报数过程...

当前从 1 开始报数：2 3 
→ 报数到 3，出列人员：3
剩余人员圈：当前人员圈：1 → 2 → 4 → 5

当前从 4 开始报数：5 1 
→ 报数到 3，出列人员：1
剩余人员圈：当前人员圈：2 → 4 → 5

当前从 2 开始报数：4 5 
→ 报数到 3，出列人员：5
剩余人员圈：当前人员圈：2 → 4

当前从 2 开始报数：4 2 
→ 报数到 3，出列人员：2
剩余人员圈：当前人员圈：4

===== 最终结果 =====
最后留下的人员：4
问题求解完成！

再次运行代码，输入：n=7，m=4，控制台输出以下内容： 输出内容截图：

输出内容文本显示：

===== 开始求解约瑟夫问题(n=7, m=4) =====
初始人员圈创建完成：当前人员圈：1 → 2 → 3 → 4 → 5 → 6 → 7

开始报数过程...

当前从 1 开始报数：2 3 4 
→ 报数到 4，出列人员：4
剩余人员圈：当前人员圈：1 → 2 → 3 → 5 → 6 → 7

当前从 5 开始报数：6 7 1 
→ 报数到 4，出列人员：1
剩余人员圈：当前人员圈：2 → 3 → 5 → 6 → 7

当前从 2 开始报数：3 5 6 
→ 报数到 4，出列人员：6
剩余人员圈：当前人员圈：2 → 3 → 5 → 7

当前从 7 开始报数：2 3 5 
→ 报数到 4，出列人员：5
剩余人员圈：当前人员圈：2 → 3 → 7

当前从 7 开始报数：2 3 7 
→ 报数到 4，出列人员：7
剩余人员圈：当前人员圈：2 → 3

当前从 2 开始报数：3 2 3 
→ 报数到 4，出列人员：3
剩余人员圈：当前人员圈：2

===== 最终结果 =====
最后留下的人员：2

至此，【数组与链表】循环链表实战 - 约瑟夫问题求解案例已全部完成。