关于平衡二叉树的理解有一些博客了,但是我觉得不能很好地理解总是有一些原因的,我自己就代表了一种开始不能理解的原因,所以从自己理解时碰到的问题来解释下,也加深下自己的印象。
感觉好难讲清楚。。如果有相关视频就好了,就像把一个数学公式用文字表达出来,会变得非常难以理解。
几种基础类型
一共4种类型,分别是L-L,L-R,R-R,R-L型,一定要对这个有一个画面式的理解,因为我们不可能背代码,这4种基础类型就是我们复现代码的最好的依据。这图是我自己画的。。。
以下图来解释L-R型的意思(其他3种类似)
1在3的左边(Left),2在1的右边(Right),故称为L-R型
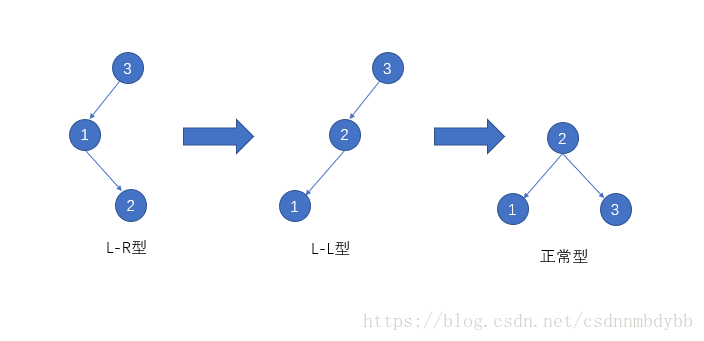
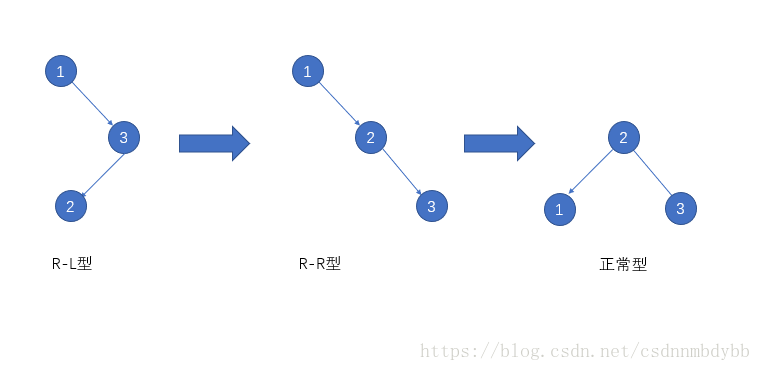
在知道这4种类型后,我们先从简单类型入手,也就是L-L和R-R型
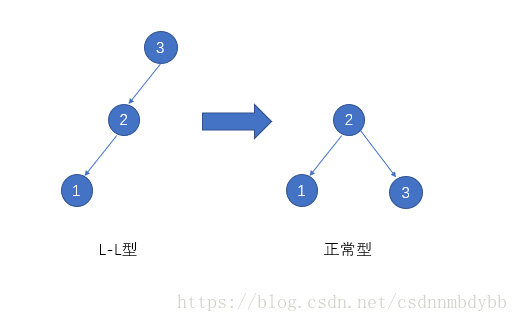
L-L型,直接对3进行右旋操作
先解释下右旋的直观理解,就是3绕着2顺时针旋转。(父节点绕着子节点顺时针旋转)
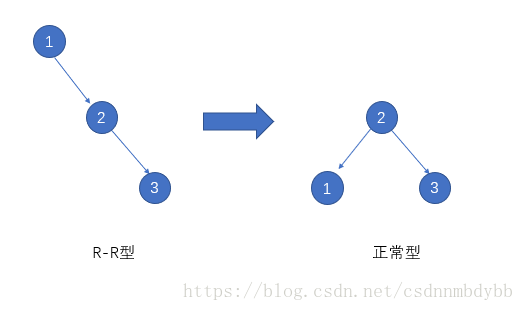
同样,对于R-R型,左旋就是1绕着2逆时针旋转。(父节点绕着子节点逆时针旋转)
node *rotateRight(node *root) {
node *t = root->left;
root->left = t->right;//托付2的右儿子
t->right = root;
return t;
}
直观的看到,2的右儿子成了3,要是2本来没有2儿子还好,如果2本来有右儿子怎么办呢?这是矛盾1;
3本来是有左儿子的,那么现在没了,3岂不是很难过???这是矛盾2;
马克思主义说过矛盾可以同归于尽,这里我们来感受下马克思主义哲学的优越性。。。
2多个右儿子,3少个左儿子,怎么办呢,2和3一拍即合,2把多出来的右儿子托付给3儿子,真的是2333333
当然了,这只是为了便于理解,但是我们可以发现,这样子也是符合线索二叉树的,因为2的右儿子必然比3小,当3的左儿子不亏。
总结:关键要理解这里的托付儿子这一步。
这里左旋也一样,本来1有右儿子,现在好像没了;2本来如果有个左儿子,那这里被1换后就多出来个左儿子;
那么,2就把多出来的左儿子拿出来当1的右儿子。
这是先左旋3的左子树1,形成我们已经解决的L-L型,然后再右旋2节点。
node *rotateLeftRight(node *root) {
root->left = rotateLeft(root->left);
return rotateRight(root);
}

R-L型类似了。




















 1976
1976










