漫画：什么是神秘的“凯利公式”？

作者 | 小灰

来源 | 程序员小灰（ID：chengxuyuanxiaohui）

(何鸿燊,1921-2020)

（约翰·拉里·凯利）

举个一个例子，比如小灰选择投注50元，那么：

有60%的几率，他能够赢回100元，也就是净赚50元；

有40%的几率，他会输掉这份投注，也就是净亏损50元。

凯利公式究竟是什么样子呢？看起来非常简单：

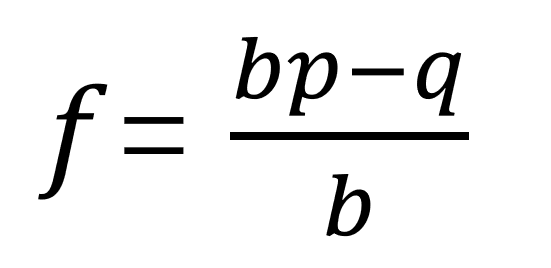
在公式当中，

• p 代表每一场获胜的几率

• q 代表每一场失败的几率（q=1-p）
  

• b 代表“赔率”，也就是盈亏比

• f 代表每次下注金额占总资金的百分比

我们把刚才的例子带入公式来算一算：

由于胜率是60%，失败的几率是1-60%=40%，所以p=60%，q=40%

假如投注50元，赢了可以收回100元，净赚50元，输了净亏50元，那么赔率就是1:1，b=1（注意：计算赔率是用 净收入/净亏损，网上有些文章搞错了，把这种情况的赔率当成了2:1）

带入公式当中：

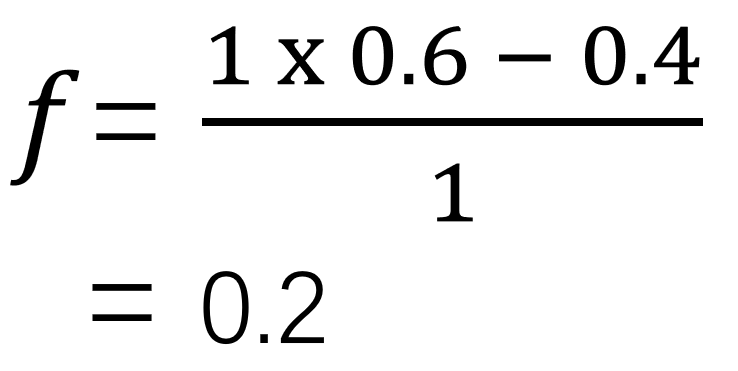
因此，当我们有100元的时候，我们的最优策略是一次投入总资金的20%，也就是20元。

如果我们幸运地赢了一场，总资金变成120元，那么下一次我们投入的金额就是120元的20%，也就是24元。

比如，张三和李四要进行一场拳击比赛，即使你知道张三比李四更厉害，但你仍然无法精确量化出，张三打赢李四的几率是多少。

想看更多小灰用漫画讲算法？可以戳下方小程序查看：

更多精彩推荐
☞尤雨溪：重头来过的 Vue 3 带来了什么？
☞原来 Kylin 的增量构建，大有学问！ | 原力计划
☞可怕！CPU 竟成了黑客的帮凶！
☞如何用NLP辅助投资分析？三大海外机构落地案例详解
☞这 10 个云计算错误，会让你的业务一蹶不振！
☞好扑科技结合区块链行业发展趋势，重磅推出“好扑区块链合伙人”计划
点击阅读原文，精彩继续。
你点的每个“在看”，我都认真当成了喜欢