漫画：什么是红黑树？（下篇）

作者 | 小灰

来源 | 程序员小灰（ID：chengxuyuanxiaohui）

上周，我们初步介绍了红黑树存在的意义，以及红黑树的插入操作，没看过的小伙伴可以点击下面链接：

漫画：什么是红黑树？

今天，我们来继续介绍红黑树的删除操作，以及红黑树和其他平衡二叉树的比较。

二叉查找树是如何进行删除操作的呢？可以分成三种情况。

情况1，待删除的结点没有子结点：

上图中，待删除的结点12是叶子结点，没有孩子，因此直接删除即可：

情况2，待删除的结点有一个孩子：

上图中，待删除的结点13只有左孩子，于是我们让左孩子结点11取代被删除的结点，结点11以下的结点关系无需变动：

情况3，待删除的结点有两个孩子：

上图中，待删除的结点5有两个孩子，这种情况比较复杂。此时，我们需要选择与待删除结点最接近的结点来取代它。

上面的例子中，结点3仅小于结点5，结点6仅大于结点5，两者都是合适的选择。但习惯上我们选择仅大于待删除结点的结点，也就是结点6来取代它。

于是我们复制结点6到原来结点5的位置：

被选中的结点6，仅大于结点5，因此一定没有左孩子。所以我们按照情况1或情况2的方式，删除多余的结点6:

红黑树的特性（规则）如下：

1.结点是红色或黑色。

2.根结点是黑色。

3.每个叶子结点都是黑色的空结点（NIL结点）。

4.每个红色结点的两个子结点都是黑色。(从每个叶子到根的所有路径上不能有两个连续的红色结点)

5.从任一结点到其每个叶子的所有路径都包含相同数目的黑色结点。

下面我们通过一个例子，来看一看删除红黑树的结点会对规则产生怎样的影响：

上图的这颗红黑树，待删除的是黑色结点1，有一个右孩子。根据二叉查找树的删除流程，我们让右孩子结点6直接取代结点1：

显然，这颗新的二叉树打破了两个规则：

规则4. 每个红色结点的两个子结点都是黑色。

规则5. 从任一结点到其每个叶子的所有路径都包含相同数目的黑色结点。

第一步：如果待删除结点有两个非空的孩子结点，转化成待删除结点只有一个孩子（或没有孩子）的情况。

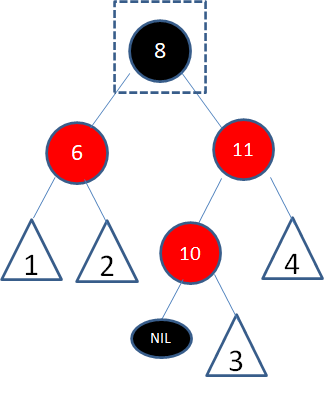
上面例子是一颗红黑树的局部，标数字的三角形代表任意形态的子树，假设结点8是待删除结点。

根据上文讲解的二叉查找树删除流程，由于结点8有两个孩子，我们选择仅大于8的结点10复制到8的位置，结点颜色变成待删除结点的颜色：

接下来我们需要删除红色的结点10：

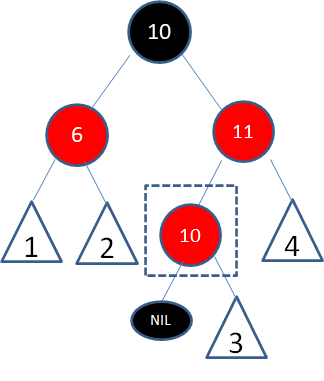
红色结点10能成为仅大于8的结点，必定没有左孩子结点，所以问题转换成了待删除结点只有一个右孩子（或没有孩子）的情况。接下来我们进入第二步。

第二步：根据待删除结点和其唯一子结点的颜色，分情况处理。

情况1，自身是红色，子结点是黑色：

这种情况最简单，按照二叉查找树的删除操作，删除结点1即可：

情况2，自身是黑色，子结点是红色：

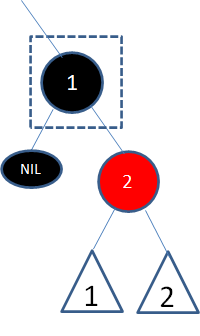
这种情况也很简单，首先按照二叉查找树的删除操作，删除结点1：

此时，这条路径凭空减少了一个黑色结点，那么我们把结点2变成黑色即可：

情况3，自身是黑色，子结点也是黑色，或者子结点是空叶子结点：

这种情况最复杂，涉及到很多变化。首先我们还是按照二叉查找树的删除操作，删除结点1：

显然，这条路径上减少了一个黑色结点，而且结点2再怎么变色也解决不了。

这时候我们进入第三步，专门解决父子双黑的情况。

第三步：遇到双黑结点，在子结点顶替父结点之后，分成6种子情况处理。

子情况1，结点2是红黑树的根结点：

此时所有路径都减少了一个黑色结点，并未打破规则，不需要调整。

子情况2，结点2的父亲、兄弟、侄子结点都是黑色：

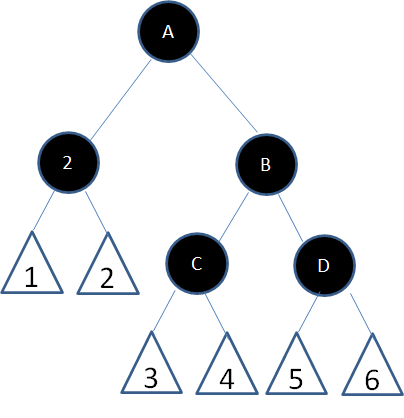
此时，我们直接把结点2的兄弟结点B改为红色：

这样一来，原本结点2所在的路径少了一个黑色结点，现在结点B所在的路径也少了一个黑色结点，两边“扯平”了。

可是，结点A以下的每一条路径都减少了一个黑色结点，与结点A之外的其他路径又造成了新的不平衡啊？

没关系，我们让结点A扮演原先结点2的角色，进行递归操作，重新判断各种情况。

子情况3，结点2的兄弟结点是红色：

首先以结点2的父结点A为轴，进行左旋：

然后结点A变成红色、结点B变成黑色：

这样的意义是什么呢？结点2所在的路径仍然少一个黑色结点呀？

别急，这样的变化有可能转换成子情况4、5、6中的任意一种，在子情况4、5、6当中会进一步解决。

子情况4，结点2的父结点是红色，兄弟和侄子结点是黑色：

这种情况，我们直接让结点2的父结点A变成黑色，兄弟结点B变成红色：

这样一来，结点2的路径补充了黑色结点，而结点B的路径并没有减少黑色结点，重新符合了红黑树的规则。

子情况5，结点2的父结点随意，兄弟结点B是黑色右孩子，左侄子结点是红色，右侄子结点是黑色：

这种情况下，首先以结点2的兄弟结点B为轴进行右旋：

接下来结点B变为红色，结点C变为黑色：

这样的变化转换成了子情况6。

子情况6，结点2的父结点随意，兄弟结点B是黑色右孩子，右侄子结点是红色：

首先以结点2的父结点A为轴左旋：

接下来让结点A和结点B的颜色交换，并且结点D变为黑色：

这样是否解决了问题呢？

经过结点2的路径由（随意+黑）变成了（随意+黑+黑），补充了一个黑色结点；

经过结点D的路径由（随意+黑+红）变成了（随意+黑），黑色结点并没有减少。

所以，这时候重新符合了红黑树的规则。

以上就是红黑树删除的全过程。

给定下面这颗红黑树，待删除的是结点17：

第一步，由于结点17有两个孩子，子树当中仅大于17的结点是25，所以把结点25复制到17位置，保持黑色：

接下来，我们需要删除原本的结点25：

这个情况正好对应于第二步的情况三，即待删除结点是黑色，子结点是空叶子结点。

于是我们删除框框中结点25，进入第三步：

此时，框框中的结点虽然是空叶子结点，但仍然可以用于判断局面，当前局面符合子情况5的镜像：

于是我们通过左旋和变色，把子树转换成情况6的镜像：

再经过右旋、变色，子树最终成为了下面的样子：

这样一来，整颗二叉树又重新符合了红黑树的规则。

更多精彩推荐
☞登 GitHub 趋势榜首德国疫情追踪 App 号称可保疫情隐私数据无忧，你信吗？
☞百度否认退市；微信官方回应「个人影响度报告」；微软公布 C# 9.0 计划 | 极客头条
☞200 万年薪请不到！清华姚班到底有多牛？| 原力计划
☞出任 Twitter 独立董事，AI 女神李飞飞的传奇人生
☞我们已经不用AOP做操作日志了！ | 原力计划
☞从特斯拉CEO到推特CEO ，细数这9位持有比特币的顶级富豪
你点的每个“在看”，我都认真当成了喜欢