二叉树算法day31-38

二叉树算法
day31
1.已知一颗二叉树，按照顺序存储结构进行存储，设计一个算法，求编号分别i和j的两个节点的最近的公共祖先结点的值。
思想：
祖先结点的下标为（i>j / j>i）i/2或者j/2
已知一个祖先结点，其儿子结点的下标为i*2

typedef ElemType int; 
ElemType Search_Common_Ancester(int A[], int i,int j){

if(A[i] != NULL && A[j] != NULL){

	//设置起始条件
	while(i != j){
		if(i > j){
			i = i/2;//进行寻找祖先
		}else{
			j = j/2;//进行交换
		}
	}
	//这里退出了循环，因此有i=j
	return A[i];//返回结果
}
	
}

二叉树中序遍历-----非递归实现
口诀：入栈向左一直走 出栈访问右子树

算法思路：

1.初始化一个数据结构栈
2.对于从根节点开始，依次入栈左子树的左节点，直到结点为NULL，
3.同时对其进行栈顶元素的出栈
4.出栈之前要先判断右子树是否存在
5.右子树存在则入栈
6.不存在则出栈并访问。

typedef struct TNode{
	 ElemType data;
	 struct TNode* lchild, *rchild;
}TNODE;
//中序遍历
void MiddleTraverse(Tree root){

	InitStack(S);
	root =  p;
//起始条件
	while(p != NULL ｜｜ !isEmpty(S)){
		if(p != NULL){
		//入栈向左一直走
		push(S,p);

		p = p->lchild;//左孩子不空 一直向左走

	}else{//当到达空结点
		pop(S,p);//栈顶元素出站并访问

		visit(p->data);

		p = p->rchild;//向右子树

	  }
	}
}

二叉树后序遍历----非递归！！！
二叉树的后序遍历是三种遍历序列中非递归实现最为困难的一个，需要对出栈元素进行多次判断，这里以上面的二叉树的进行分析：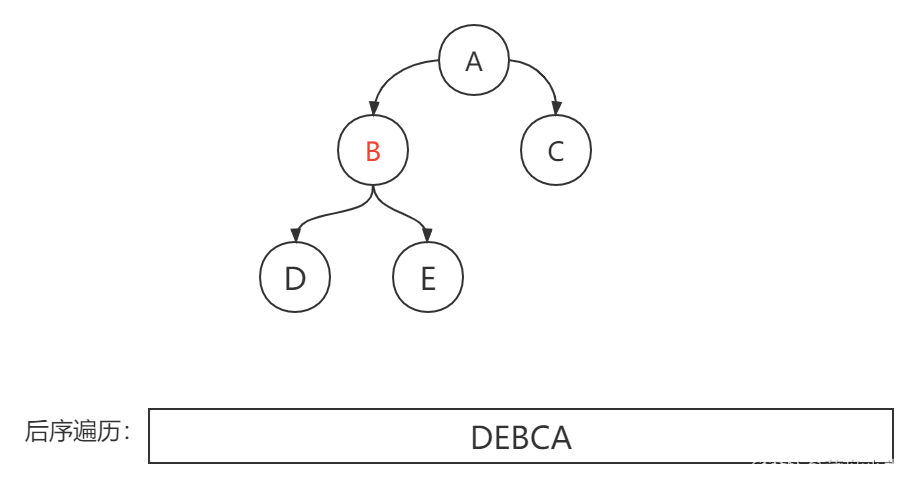
后序遍历的实现依旧是需要借助于数据结构栈进行操作，因此我们试着先将其左子树入栈，向左一直走如下图：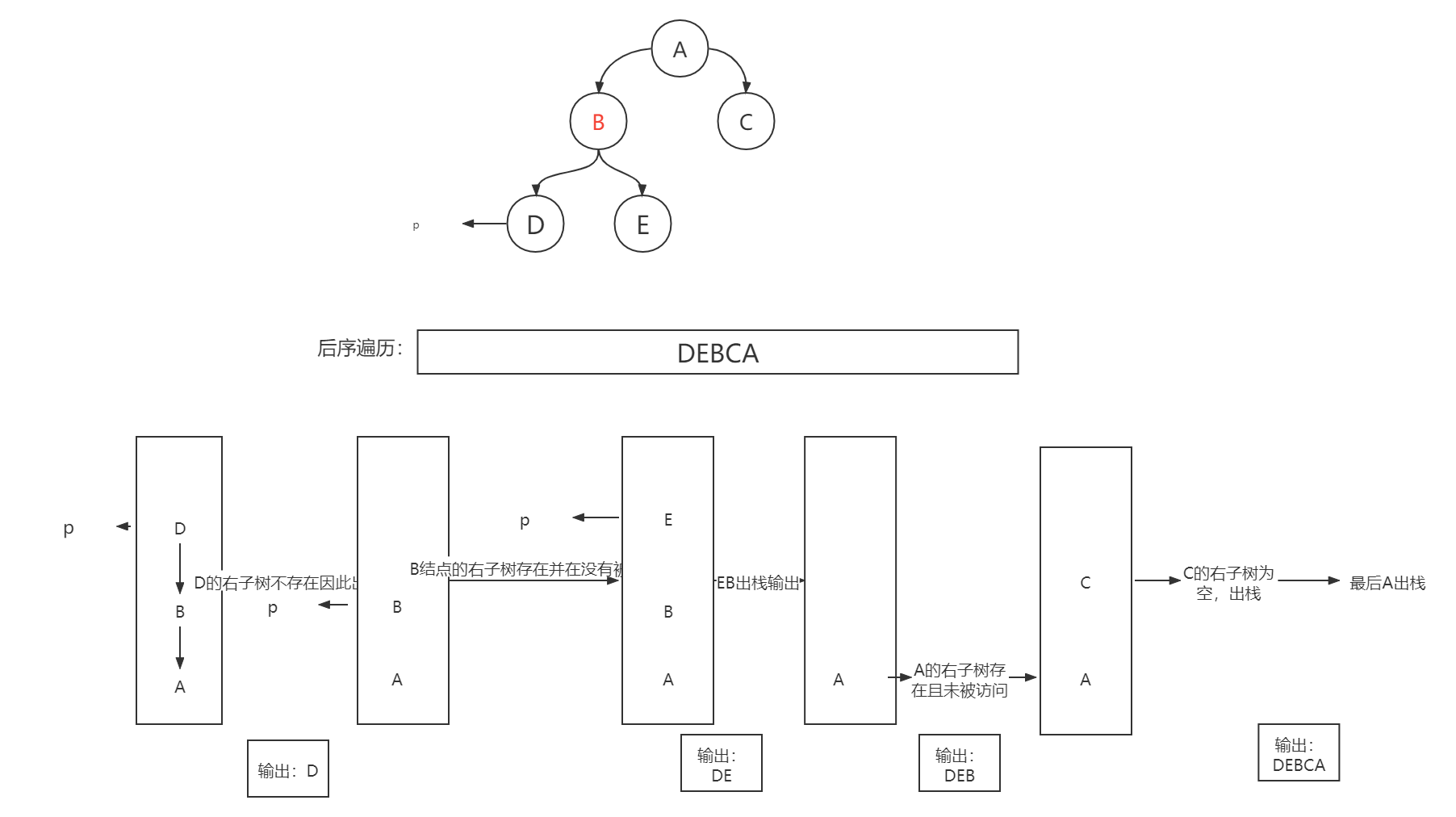
大致实现的思路便是：

1.入栈左子树直到左子树为NULL
2.获取到栈顶的结点p-----采用GetTop(S,p)
3.对栈顶的结点进行右子树是否访问以及是否为NULL的检测，
！！！！！！！！！！记住！！！
4.这里是对栈顶结点的右子树的是否为空和是否之前被访问过进行判断。
5.若不为空也没有被访问到，则该元素进栈，指向其左子树进行判断
6.若为空或者已经被访问到了，则栈顶元素直接出栈，并设置标记已经访问过
循环这个过程。

助记口诀：入栈向左一直走，判定(右子树)，出栈访问，标记，重置初始指针

typedef struct TNode{
	 ElemType data;
	 struct TNode* lchild, *rchild;
}TNODE,*BiTree;
//非递归方法实现后序遍历
void OrderTaverse(BiTree root){
	if(root == NULL){
		return ;
	}
	InitStack(S);//初始化一个栈
	TNode * p = root;//操作指针
	TNode * r = NULL;//标记访问指针

	while(! isEmpty(S)){
		//核心代码
		if(p!=NULL){
			//入栈向左一直走
			push(S,p);//入栈
			p = p->lchild;
		}else{
			//这时p为空，说明左子树走到尽头了
			GetTop(S,p);//获取栈顶元素
			//对栈顶元素进行检测
			if(p->rchild != NULL && p->rchild != r){//不为空，没有被访问
				p = p->rchild;//转到右子树
				push(S,p);//入栈
				p = p->lchild;//左子树继续

			}else{
				//若已经被访问
				pop(S,p);//出栈
				visit(p->data);//访问
				r = p;//标记已经访问
				p=NULL;//重置为NULL方便下一次使用
			}
		}
	}
}

二叉树层次遍历非递归实现

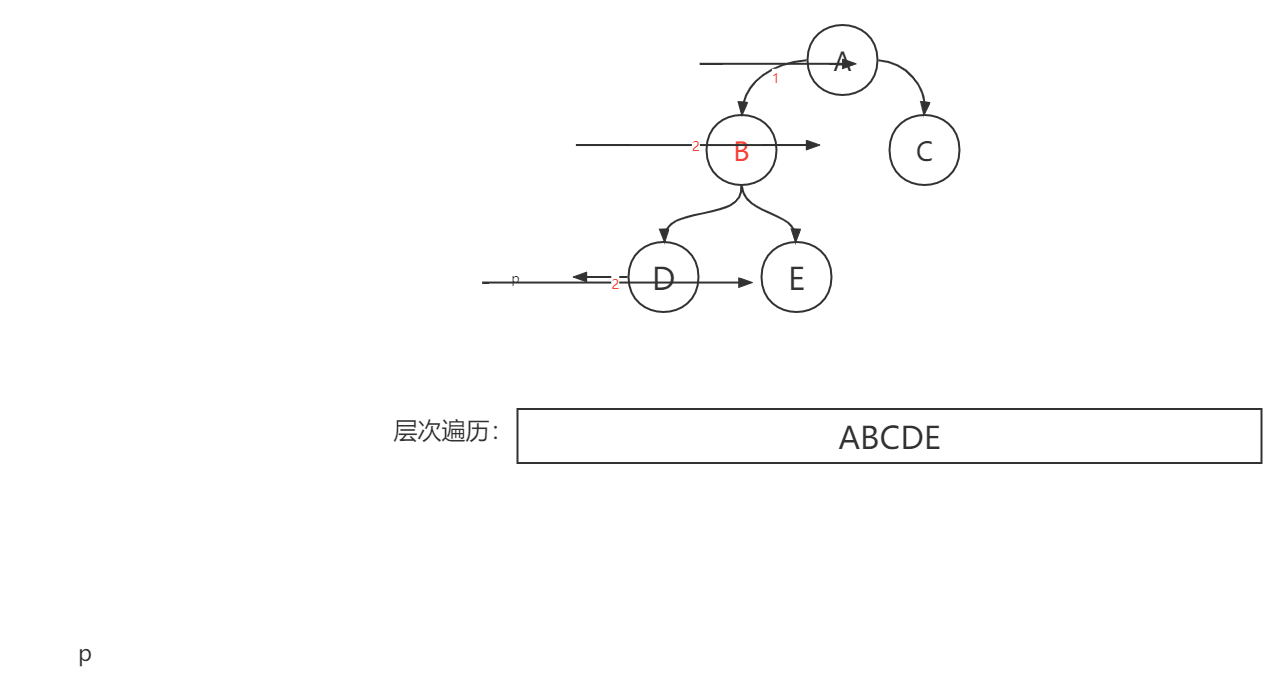
结合其二叉树的递归实现顺序，我们发现，这个实现的遍历结果采用队列的方式，对于其先进先出的特性非常符合，因此层次遍历采用队列实现

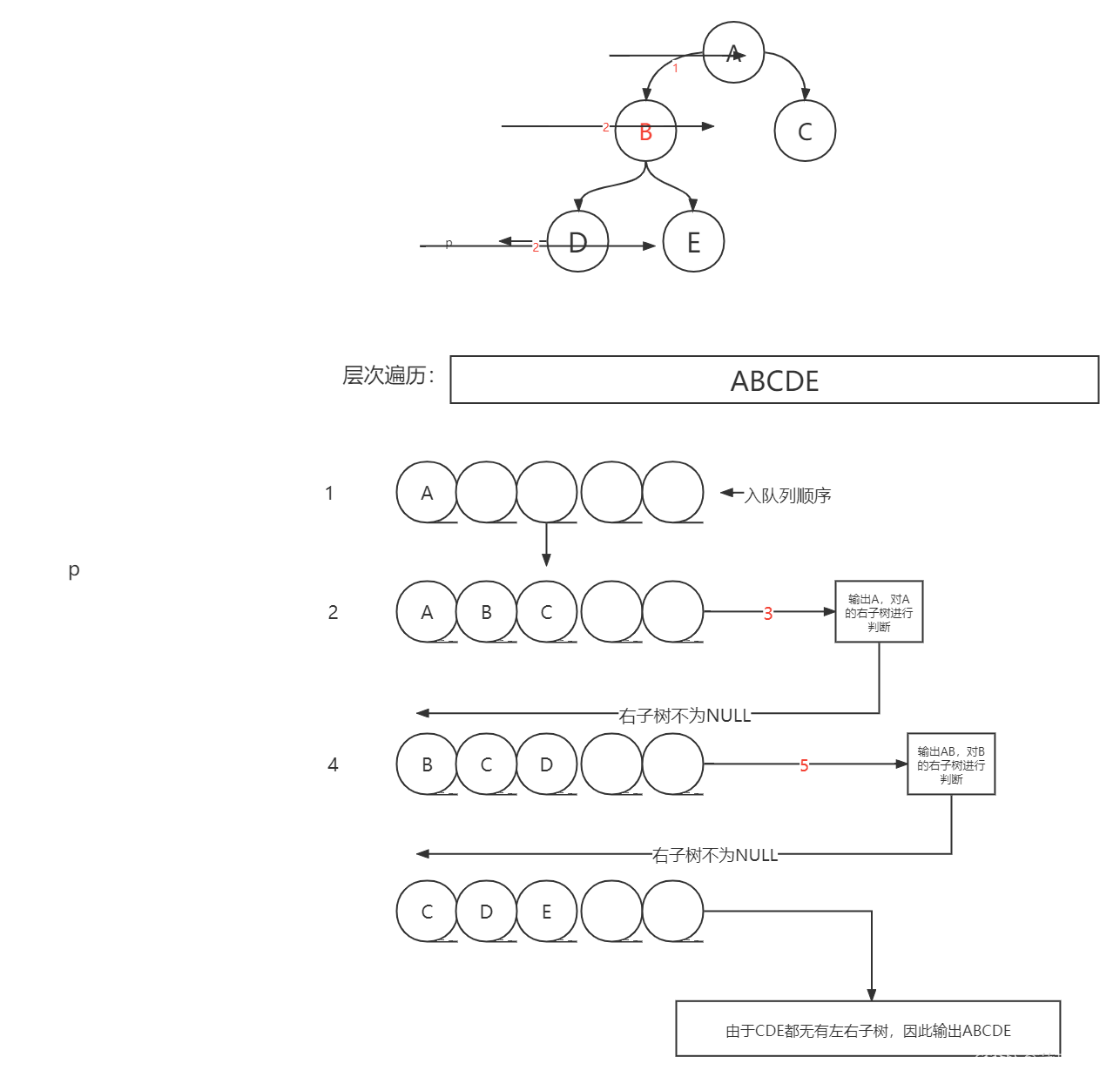
实现思路：

根节点判断是否为NULL
根节点入队，
出队访问左右子树
若左子树不为空，则访问左子树
若右子树不为空，访问右子树
队列为空，则循环停止
实现核心代码如下：
口诀：入队出队访问有左入左，有右入右

typedef struct TNode{
	 ElemType data;
	 struct TNode* lchild, *rchild;
}TNODE,*BiTree;
//层次遍历代码
void BehindTraverse(BiTree root){
	if(root == NULL){
		return ;
	}
	InitQueue(Q);//初始化队列
	TNODE *p;

	//根节点如队列
	EnterQueue(Q,root);

	while(!isEmpty(Q)){
		DeQueue(Q,p);//出队列
		visit(p->data);//访问数据
		//有左子树入队列
		if(p->lchild != NULL){
			EnterQueue(Q,p->lchild);
		}
		//右子树入队列
		if(p->rchild != NULL){
			EnterQueue(Q,p->rchild);
		}
	}
}

day38二叉树至下而上，从右向左的层次遍历算法

算法思想：利用原本的层次遍历算法 出队的同时将各个节点入栈，再依次出栈

根据以上的基础遍历代码，我们对其进行改进，由于要求如下：

从上而下----------层次遍历可以保证
从右至左----------需要一个辅助数据结构进行设计

总的来说执行过程就是：

根节点入队
队列不为空–根节点出队-----入栈
对根节点的左右子树的NULL进行判断，
不为NULL则进入队列，入栈
循环执行以上过程

typedef struct TNode{
	 ElemType data;
	 struct TNode* lchild, *rchild;
}TNODE,*BiTree;
//改进层次遍历算法
void levelOrder(BiTree * root){
	InitStack(S);
	InitQueue(Q);//初始化队列
	BiTree * p = root;
	if(p != NULL){
		EnterQueue(Q,p);//入队列
		while(! isEmpty(Q)){//队列不为空
			DeQueue(Q,p);//出队列
			push(S,p);//压入栈中
			if(p->lchild != NULL){
				EnterQueue(Q,p->lchild);//若左子树不为NULL，入队列左子树
			}
			if(p->rchild != NULL){
				EnterQueue(Q,p->rchild);//若右子树不为NULL，入队列右子树
			}
		}
	}
	//进行从右至左的输出
	while(! isEmpty(S)){
		pop(S,p);
		visit(p->data);//进行访问
	}
}

相比于之前的基础层次遍历序列，其改进的地方就是在下面：

	DeQueue(Q,p);//出队列
	push(S,p);//压入栈中


	//进行从右至左的输出
	while(! isEmpty(S)){
		pop(S,p);
		visit(p->data);//进行访问
	}