Python数据分析实战：日常工作必备可视化图表_数据分析实例代码加截图-优快云博客

本文链接：https://blog.youkuaiyun.com/csdn1561168266/article/details/143774464

大家好，数据分析是利用数学、统计学与实践相结合的科学统计分析方法，对excel数据、数据库中的数据、收集大量数据、网页抓取的数据进行分析，从中提取有价值的信息并形成结论进行展示的过程。本文将介绍数据分析常用可视化方法，并通过示例展示如何使用Python进行数据探索。

为了方便可视化图表操作展示，使用Kaggle上的高热数据集：红酒质量数据，可在Kaggle直接下载（搜索winequality-red.csv）：

该数据集包含葡萄牙“Vinho Verde”红酒的理化特性（输入变量）和感官评分（输出变量）, 适合用于数据探查、机器学习（分类或回归）等分析任务的练习。

读入数据后，先利用.describe() 查看数据分布情况：

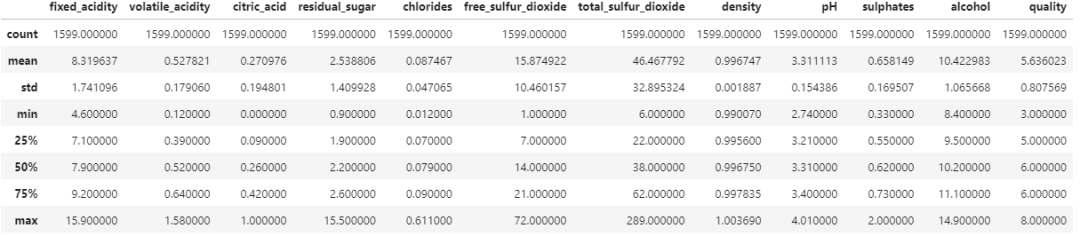
通过.describe() 直观得到各数值型变量的分布情况，如均值、标准差、最小值、最大值。以下是一些日常分析工作中常用可视化方法，附代码和输出示例。

1.直方图(Histogram)

直方图用于查看单个变量的分布情况，常用于了解变量的偏态（左偏/右偏）、集中趋势和离群点分布。当想快速了解数据中的值是如何分布的，直方图就非常实用。

# 创建 4 行 3 列的图布局，方便一次性看到所有的变量直方图
fig, axes = plt.subplots(nrows=4, ncols=3, figsize=(20, 20))

# 遍历红酒数据集的每个字段，绘制直方图
for index, column in enumerate(data.columns):
    ax = axes.flatten()[index]
    ax.hist(data[column], color=colors[index], bins=20, edgecolor='black', alpha=0.7, label=column)
    ax.legend(loc="best", fontsize=12)
    ax.set_title(f"Distribution of {column}", fontsize=14)
    ax.set_xlabel(column, fontsize=12)
    ax.set_ylabel("Frequency", fontsize=12)
    ax.grid(True, linestyle='--', alpha=0.6)

plt.suptitle("Wine Dataset Histograms", size=24, y=1.02)
plt.tight_layout(rect=[0, 0, 1, 0.98])
plt.show()

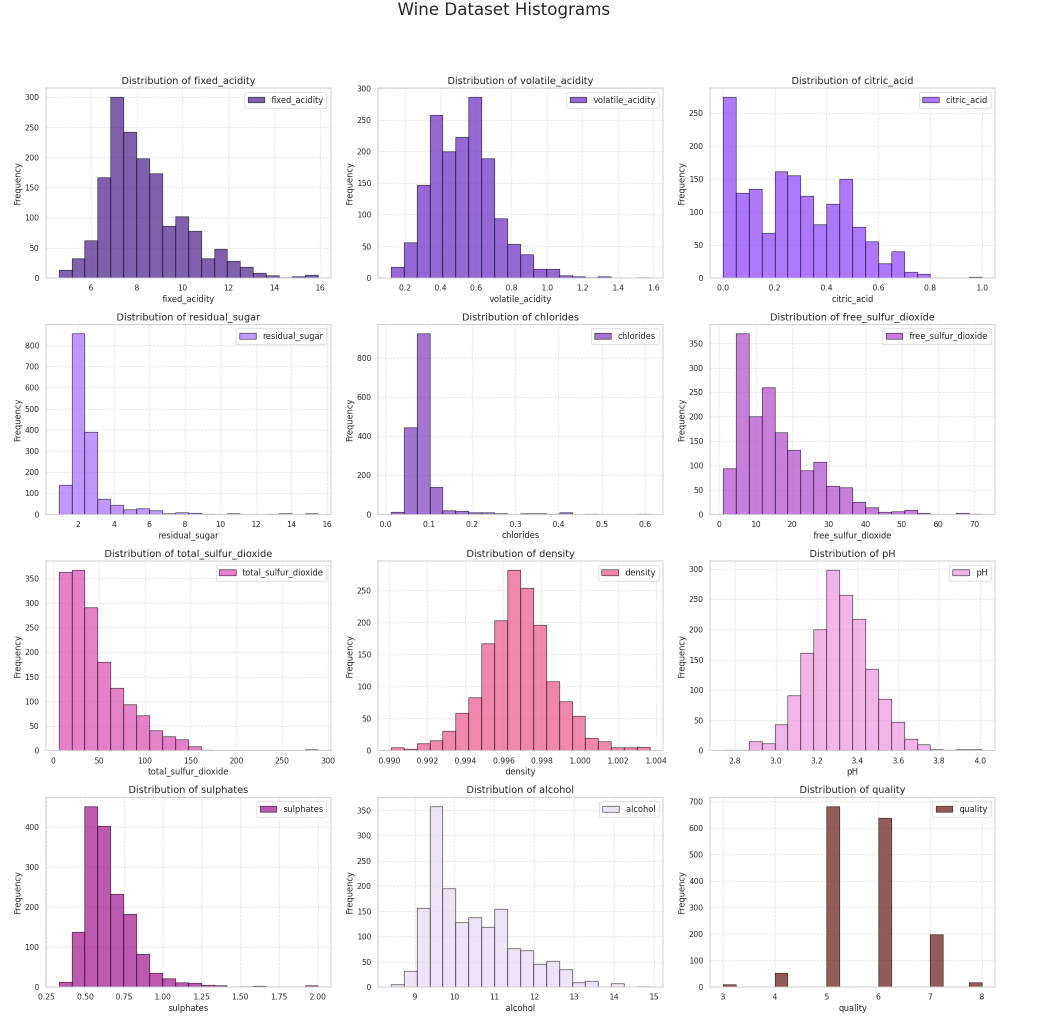
以上直方图展示了数据中各变量的取值频率分布。

直方图解读方法：柱子高度代表频数（某个范围内的样本数量），宽度代表值的范围（bins）；观察数据分布是否正态，是否有明显的偏态；离群点会显示为图中稀疏的区块。

2.箱线图(Boxplot)

箱线图展示数据集的五数概括（最小值、下四分位数（Q1）、中位数（Q2）、上四分位数（Q3）、最大值）以及离群点。箱线图的作用有以下方面：

检测离群值：通过“胡须”之外的点（通常为1.5倍四分位范围外的值），快速识别异常值。
比较不同组别：比对多个组的数据分布差异和集中趋势规律。
观察数据偏态：通过箱体及“胡须”的对称性，观察数据的偏态（偏左、偏右或对称）。

以下展示酒精含量、质量得分两个变量之间的关系：

plt.figure(figsize=(8, 6))
sns.set_theme(style="darkgrid")
sns.boxplot(x='quality', y='alcohol', data=data, palette='viridis')
plt.title('Alcohol Content vs Wine Quality')
plt.show()

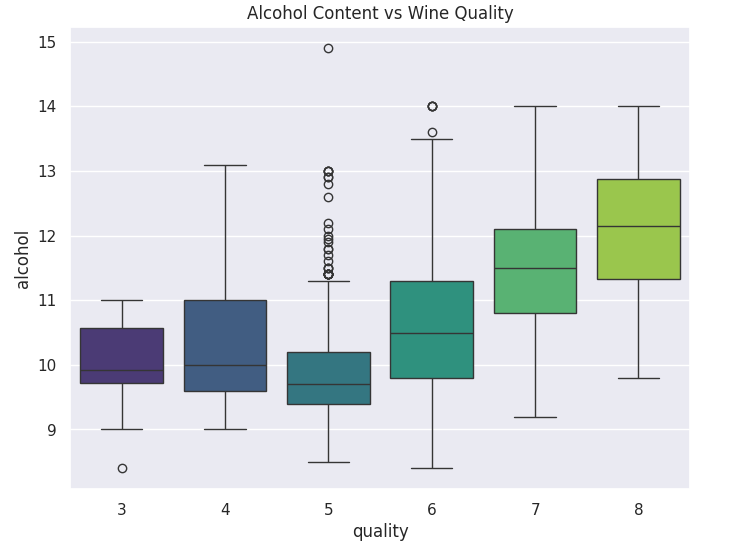
中位数（Median）：箱线图中间的线，表示数据的中位数。可以看到数据的中心位置。如果中位数偏向上或下，数据可能存在偏态。

四分位数范围（IQR）：箱子的上下边界分别是第一四分位数(Q1，25%)和第三四分位数(Q3，75%)。箱子长度(Q3-Q1)称为四分位数范围 (IQR)，代表数据的分布范围。箱子越长数据变异性越大，箱子越短数据越集中。

胡须（Whiskers）：从箱子延伸出的直线，通常延伸到Q1-1.5 IQR和Q3+1.5 IQR 之间的数据范围。胡须之外的点被认为是异常值。胡须的长度表示数据的整体范围，长度不平衡表明数据分布不对称。

异常值（Outliers）：胡须之外的点为异常值或离群点，代表数据中极端情况。

多箱线图对比：如果在同一图中绘制了多个箱线图，可以通过中位数位置、IQR大小和异常值来比较不同组别的差异（箱与箱的位置差异展示组中心趋势差异）。

3.相关性热力图

相关性热力图展示变量间的相关性矩阵。颜色深浅代表相关性强弱：颜色越深，表示相关性越强。其中data.corr()计算相关性系数。该图适用于发现变量间的线性关系，为数据洞察以及后续的特征选择、建模提供依据。

plt.figure(figsize=(12, 8))
sns.heatmap(data.corr(), annot=True, cmap='coolwarm', linewidths=0.5) # 绘制相关性热图
plt.title('Data Correlation Heatmap')
plt.show()

4.成对变量关系图(Pairplot)

配对图通常用于探索数据集中多个变量之间的关系，通过散点图和直方图快速发现潜在的模式或异常值。下图中展示的是以下两个变量之间的关系：volatile_acidity（挥发酸度）和quality（质量评分），不同颜色表示不同的评分组。

sns.pairplot(data, vars=["volatile_acidity", "quality"],hue="quality")

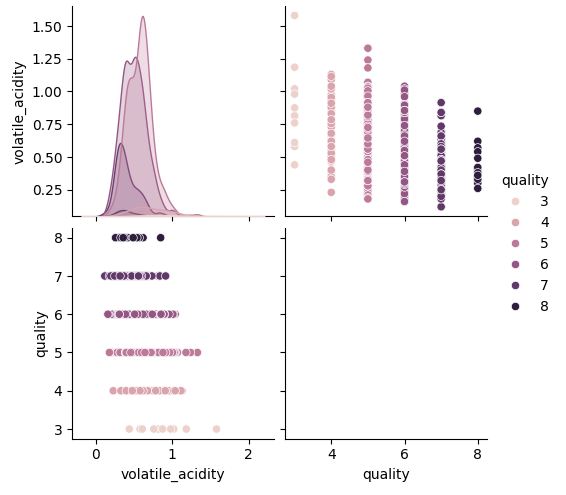
左上角（密度图）：显示挥发酸度（volatile_acidity）的核密度估计（KDE）图，描述其分布。曲线的高低表示酸度值（0-2）在数据中的密集程度。我们看到大部分数据集中在0.25到1.25之间，并且不同质量评分的数据有重叠，但总体呈现出左偏的分布。

右上角与左下角（散点图）：展示volatile_acidity与quality之间的散点关系。每个点的颜色和大小代表质量评分，位置表示挥发酸度与质量的对应关系。可以看出，挥发酸度与质量评分呈负相关，较低的挥发酸度低可能助于提升酒的感官评分。随着挥发酸度的增加，评分略有下降的趋势。

右下角：因为这是变量与自身的关系，在Pairplot中通常是空白或对角线位置。

5.成对变量关系图(多变量版)

在两变量基础上增加新变量，可观察多个变量之间的互动关系，发现更复杂的模式。如下所示，这里不仅展示了挥发酸度，还增加了柠檬酸、残留糖分等多个变量，并使用 palette="Spectral" 调整了颜色，markers 则改变了点的形状。

sns.set(style="whitegrid")
pairplot = sns.pairplot(data, vars=["volatile_acidity", "citric_acid", "residual_sugar", "quality"],
                        hue="quality", palette="Spectral", markers=["o", "s", "D", "P", "X", "*"],
                        diag_kind="kde", height=3, aspect=1.2, plot_kws={'alpha':0.6})
pairplot.fig.suptitle("Pairplot of Wine Quality Features", y=1.02)
plt.show()

以上就是几个高频使用的数据分析可视化，下面补充多维度可视化示例，用于三维空间的数据洞察。

6.三维散点图探索多变量关系

3D散点图用于在三维空间中可视化三个变量之间的关系，可进行三个连续变量的关系展示，适合用于发现数据中的聚类、趋势或离群点。此例展示了酒精含量（alcohol）、pH 值（pH）和硫酸盐含量（sulphates）的交互关系，有助于观察数据的分布、是否存在成簇聚类。

fig = plt.figure(figsize=(12, 10))
ax = fig.add_subplot(111, projection='3d')
# 为每个数据点生成随机颜色
colors = np.random.rand(len(data)) 
scatter = ax.scatter(data['alcohol'], 
data['pH'], data['sulphates'], c=colors, cmap='hsv', s=100, alpha=0.7)
plt.show()

7.三维螺旋直方图

螺旋直方图可展示数据的多个特征在三维空间中的分布情况，每根立柱表示数据某个特征的值或频率，也可用于展示周期性或循环性的时间序列数据。

fig = plt.figure(figsize=(14, 10))
ax = fig.add_subplot(111, projection='3d')

# 为每个变量创建 3D 螺旋直方图
for index, column in enumerate(data.columns[:12]):
    values = data[column].values[:100]
    ax.bar3d(x, y, z, dx=0.05, dy=0.05, dz=values, color=colors[index], alpha=0.7)
plt.show()