KMP、Trie树 、AC自动机‌ ，三大算法实现 优雅 过滤敏感词

尼恩说在前面：

在40岁老架构师 尼恩的读者交流群(50+)中，最近有小伙伴拿到了一线互联网企业如得物、阿里、滴滴、极兔、有赞、shein 希音、shopee、百度、网易的面试资格，遇到很多很重要的面试题：

• IM 敏感词过滤, 方案有哪些？
• 10万QPS下如何保证过滤延迟<50ms？
• 如何设计支持实时更新的敏感词服务？
• 10万QPS，如何设计敏感词服务，还要支持 实时更新的？

前几天 小伙伴面试阿里，遇到了这个问题。但是由于 没有回答好，导致面试挂了。

小伙伴面试完了之后，来求助尼恩。那么，遇到 这个问题，该如何才能回答得很漂亮，才能 让面试官刮目相看、口水直流。

所以，尼恩给大家做一下系统化、体系化的梳理，使得大家内力猛增，可以充分展示一下大家雄厚的 “技术肌肉”，让面试官爱到 “不能自已、口水直流”，然后实现”offer直提”。

当然，这道面试题，以及参考答案，也会收入咱们的 《尼恩Java面试宝典》V145版本PDF集群，供后面的小伙伴参考，提升大家的 3高 架构、设计、开发水平。

最新《尼恩 架构笔记》《尼恩高并发三部曲》《尼恩Java面试宝典》的PDF，请关注本公众号【技术自由圈】获取，后台回复：领电子书

IM 敏感词过滤方案有哪些？

敏感词过滤功能在很多地方都会用到，理论上在Web应用中，只要涉及用户输入的地方，都需要进行文本校验，如：IM消息、XSS校验、SQL注入检验、敏感词过滤等。今天着重讲讲如何优雅高效地实现敏感词过滤。

敏感词过滤在IM消息、社区发帖、网站检索、短信发送等场景下是很常见的需求，尤其是在高并发场景下如何实现敏感词过滤，都对过滤算法提出了更高的性能要求，几种常见的敏感词过滤方案对比如下：

‌维度‌	暴力循环	Trie树	AC自动机
‌时间复杂度‌	O(n×m)	O(L)	O(n)
‌空间占用‌	O(1)	高(GB级)	高(需失败指针)
‌适用规模‌	≤100词	≤10万词	≥10万词

• **暴力循环‌ → ‌Trie树‌：**解决前缀共享问题
• **‌Trie树‌ → ‌AC自动机‌：**通过状态转移消除回溯‌，引入失败指针实现多模式并行匹配

暴力匹配（BF）匹配算法

此方案使用BF 算法（Brute-Force算法），或蛮力算法，是一种基础的字符串匹配算法。

简单来说就是对于要进行检测的文本，遍历所有敏感词，逐个检测输入的文本中是否含有指定的敏感词。

先引入两个术语：主串和模式串。简单来说，我们要在字符串 A 中查找子串 B，那么 A 就是主串，B 就是模式串。

作为最简单、最暴力的字符串匹配算法，BF 算法的思想可以用一句话来概括，那就是，如果主串长度为 n，模式串长度为 m，我们在主串中检查起始位置分别是 0、1、2…n-m 且长度为 m 的 n-m+1 个子串，看有没有跟模式串匹配的。图示如下：

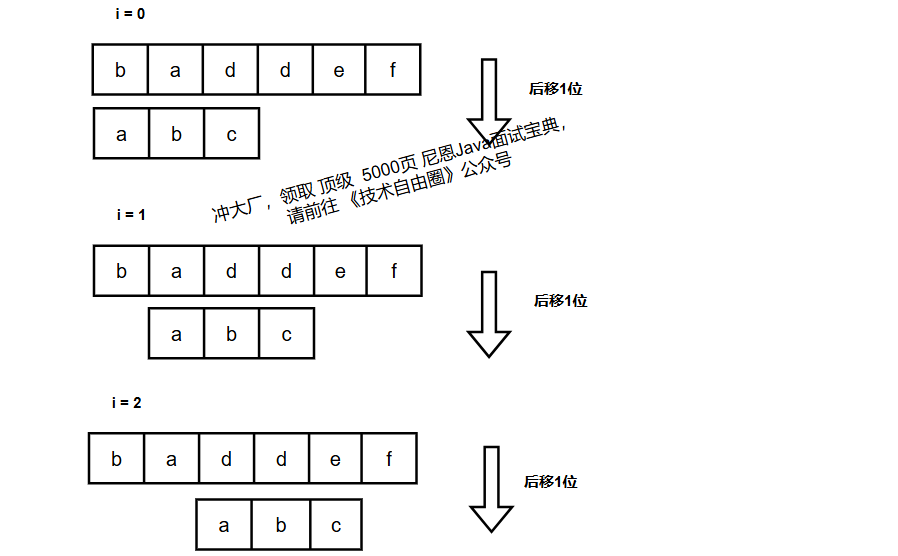
结合上图，具体来说，就是每次拿模式串和主串对齐，然后从左到右依次比较每个字符，如果出现不相等，则把模式串往后移一个位置，再次重复上述步骤，直到模式串每个字符与对应主串位置字符都相等，则返回主串对应下标，表示找到，否则返回 -1，表示没找到

这个算法很好理解，因为这就是我们正常都能想到的暴力匹配，BF 算法的时间复杂度最差是 O(n*m)（n为主串长度，m为模式串长度），意味着要模式串要移到主串 n-m 的位置上，并且模式串每个字符都要与子串比较。

尽管 BF 算法复杂度看起来很高，但是在日常开发中，如果主串和模式串规模不大的话，该算法依然比较常用，因为足够简单，实现起来容易，不容易出错。在规模不大的情况下，开销也可以接受，毕竟 O(n*m) 是最差的表现，大部分时候，执行效率比这个都要高。

但是对于对时间要求比较敏感，或者需要高频匹配，数据规模较大的情况下，比如编辑器中的匹配功能、敏感词匹配系统等，BF 算法就不适用了。

参考实现：

@Test
    public void test1(){
   
   
        Set<String>  sensitiveWords=new HashSet<>();
        sensitiveWords.add("shit");
        sensitiveWords.add("傻蛋");
        sensitiveWords.add("笨蛋");
        String text="你是傻蛋啊";
        for(String sensitiveWord:sensitiveWords){
   
   
            if(text.contains(sensitiveWord)){
   
   
                System.out.println("输入的文本存在敏感词。——" + sensitiveWord);
                break;
            }
        }
    }

暴力循环匹配 的不足

代码十分简单，也确实能够满足要求。但是这个方案有一个很大的问题是，随着敏感词数量的增多，敏感词检测的时间会呈线性增长。

由于之前的项目的敏感词数量只有几十个，所以使用这种方案不会存在太大的性能问题。但是如果项目中有成千上万个敏感词，使用这种方案就会很耗CPU了。

KMP算法(Knuth Morris Pratt 算法)

KMP 算法可以说是字符串匹配算法中最知名的算法了，KMP 算法是根据三位作者（D.E.Knuth，J.H.Morris 和 V.R.Pratt）的名字来命名的，算法的全称是 Knuth Morris Pratt 算法，简称为 KMP 算法。

与暴力匹配算法相比，KMP 算法在时间复杂度上有显著的优化，使得它在实际应用中得到了广泛的应用。

KMP 算法是一种基于 ‌**部分匹配表（next 数组）**‌ 的字符串匹配算法，通过预处理模式串的重复前后缀信息，避免主串指针回溯，将暴力匹配的最坏时间复杂度从 O(mn) 优化到 O(m+n)。

其核心思想是 ‌利用已匹配信息跳过无效比较‌，通过 next 数组确定失配时的跳转位置

KMP 算法的核心思想

假设主串是 a，模式串是 b。

在模式串与主串匹配的过程中，当遇到不可匹配的字符的时候，我们希望找到一些规律，可以将模式串往后多滑动几位，跳过那些肯定不会匹配的情况，从而避免 BF 算法这种暴力匹配，提高算法性能。

举个例子，假设：

• 主串（文本）为："ABABABCABABABD"
• 模式串（要找的词）为："ABABD"

‌**普通暴力匹配（BF算法）**‌：

(1) 主串和模式串从头开始对比： ABABA（主串） vs ABABD（模式串） ，发现 前4个字符ABAB匹配，但第5个字符A（主串）≠ D（模式串），所以，匹配失败。
(2) 暴力法会‌回退‌：主串从第2个字符B开始重新对比，模式串从头开始。

‌KMP的聪明做法‌：

1、发现前4个字符ABAB匹配，但第5个字符失败时，KMP会问：

已匹配的ABAB中，‌最长的相同 前后缀‌是什么？

• ABAB 的 前缀有： A 、AB、 ABA ；

• ABAB 的 后缀有： B、AB、BAB

最长 公共前后缀是AB，长度=2

2、直接让模式串的 AB 对齐 主串已匹配部分的 AB , 跳过无效对比：

主串：ABABABCABABABD  
        ↓   模式串从第3个字符继续匹配（`ABABD`的第3个字符`A`对齐主串`C`的位置）  
模式串：  ABABD  

• ‌主串指针不后退‌，模式串利用next数组智能跳跃。

‌关键点‌：

• next数组记录模式串的“自相似性”（比如ABAB中AB重复）。
• 匹配失败时，模式串按next值滑动，主串永不回退。

就像用尺子量布时，发现一段花纹重复，直接跳过已知重复部分继续量，省时高效

什么是 next指针

‌**next指针就像"错题本"**‌

假设你在背单词：“ABABD”（模式串），背到第5个字母时卡壳了。next指针会告诉你：

(1) 前面背对的"ABAB"里，开头的"AB"和结尾的"AB"是重复的

(2) 下次直接从第3个字母"A"开始接着背（不用重头背！）

‌具体来说‌：

• 当匹配失败时，next值告诉你：
  ✓ ‌模式串该往右滑多远‌（比如next=2，就滑到模式串第3个字符继续比）
  ✓ ‌主串不用回退‌（像传送带一样只往前走）

‌关键操作‌：next数组的生成

• 预处理模式串‌生成next数组（类似创建"跳转地图"）
• 匹配失败时 根据 next数组跳转，主串指针不后退

以模式串ABCDABD为例，计算每个位置的next值：

位置	字符	前缀	后缀	最长公共前后缀长度	next值
0	A	无	无	0	-1
1	B	A	B	0	0
2	C	A,AB	BC,C	0	0
3	D	A,AB,ABC	BCD,CD,D	0	0
4	A	A,AB,ABC,ABCD	BCDA,CDA,DA,A	1（前缀A=后缀A）	0
5	B	A,AB,…,ABCDA	BCDAB,…,B	前缀AB=后缀AB → 2	1
6	D	A,…,ABCDAB	BCDABD,…,D	0	2

‌最终next数组‌：[-1, 0, 0, 0, 0, 1, 2]

---

KMP匹配过程演示

回到最初的失败场景：

主串：ABCDABE...
模式：ABCDABD（前6字符匹配，第7字符不匹配，E≠D）

根据next数组，失败位置是模式串的第6位（索引6），对应的next[6]=2。

这意味着：

(1) ‌模式串右移位数‌ = ‌已匹配字符数 - next值‌ → 6 - 2 = 4位
(2) ‌模式串指针回退到‌ next[6]=2的位置（即模式串的第3个字符C）

‌移动后的对比‌：

主串：ABCDABE...
模式：    ABCDABD（直接从模式串的第3 个字符 `C` 开始对比）

‌对比过程‌：

• 主串的E继续和模式串的新位置 第3 个字符 C 对比（主串指针未回退！）
• 模式串的C与主串E不匹配 → 再次根据next[2]=0跳转

对比KMP和BF的效率

‌**暴力匹配（BF）**‌：

• 在第1次失败后，需要对比‌6次无效位置‌（模式串滑动1位后对比6次才能发现不匹配）

‌KMP算法‌：

• 直接跳过了4个位置，避免了这6次无效对比
• 主串指针始终向前（从位置6继续，无需回退到位置1）

把模式串想象成一个带弹簧的尺子：

(1) ‌next数组‌像是弹簧的弹力系数
(2) 每当遇到不匹配，弹簧会根据next值自动收缩到合适长度
(3) ‌主串‌像传送带一样单向移动，无需倒退重走

‌最终效果‌：KMP的时间复杂度是O(n+m)，而暴力匹配是O(n×m)！

KMP 算法的应用场景

KMP 算法的预处理阶段时间复杂度为 O(m)，其中 m 是模式串的长度。

在匹配阶段，文本串和模式串的指针都只会单向移动，不会出现回溯的情况，因此匹配阶段的时间复杂度也是 O(n + m)，其中 n 是文本串的长度。这使得 KMP 算法在处理大规模数据时具有较高的效率，相比暴力匹配算法的 O(n * m) 时间复杂度，KMP 算法在大多数情况下能够提供更快的匹配速度。

KMP 算法广泛应用于文本编辑器中的查找和替换功能、搜索引擎中的关键词匹配、生物信息学中的 DNA 序列分析等领域。例如，在文本编辑器中，当用户使用查找功能时，KMP 算法能够快速定位到目标文本的位置，从而提高用户体验。

KMP 算法作为一种经典的字符串匹配算法，凭借其高效性和稳定性，在众多领域发挥着重要作用。理解 KMP 算法的原理和实现，有助于我们更好地解决实际问题中的字符串匹配需求。

智能索引 Trie树

什么是trie树

Trie 树，也叫“字典树”。

顾名思义，它是一个树形结构。它是一种专门处理字符串匹配的数据结构，用来解决在一组字符串集合中快速查找某个字符串的问题。

我们有 6 个字符串，它们分别是：how，hi，her，hello，so，see。

我们希望在里面多次查找某个字符串是否存在。

如果使用BF算法，都是拿要查找的字符串跟这 6 个字符串依次进行字符串匹配，那效率就比较低，有没有更高效的方法呢？

这个时候，我们就可以先对这 6 个字符串做一下预处理，组织成 Trie 树的结构，之后每次查找，都是在 Trie 树中进行匹配查找。Trie 树的本质，就是利用字符串之间的公共前缀，将重复的前缀合并在一起。最后构造出来的就是下面这个图中的样子。

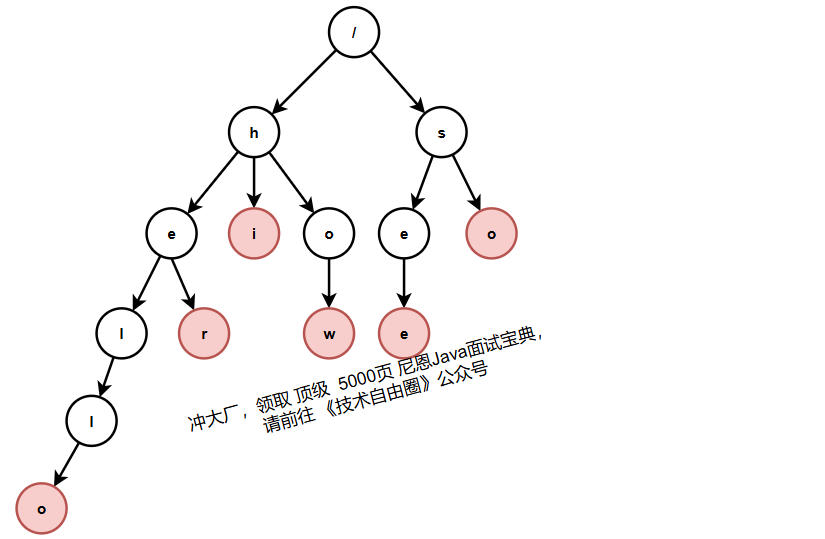
其中，根节点不包含任何信息。每个节点表示一个字符串中的字符，从根节点到红色节点的一条路径表示一个字符串（注意：红色节点并不都是叶子节点）。

Trie 树是怎么构造出来的？

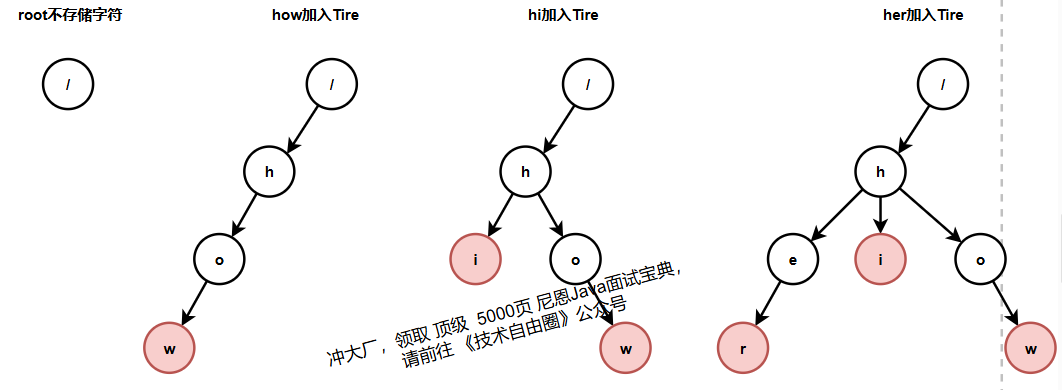
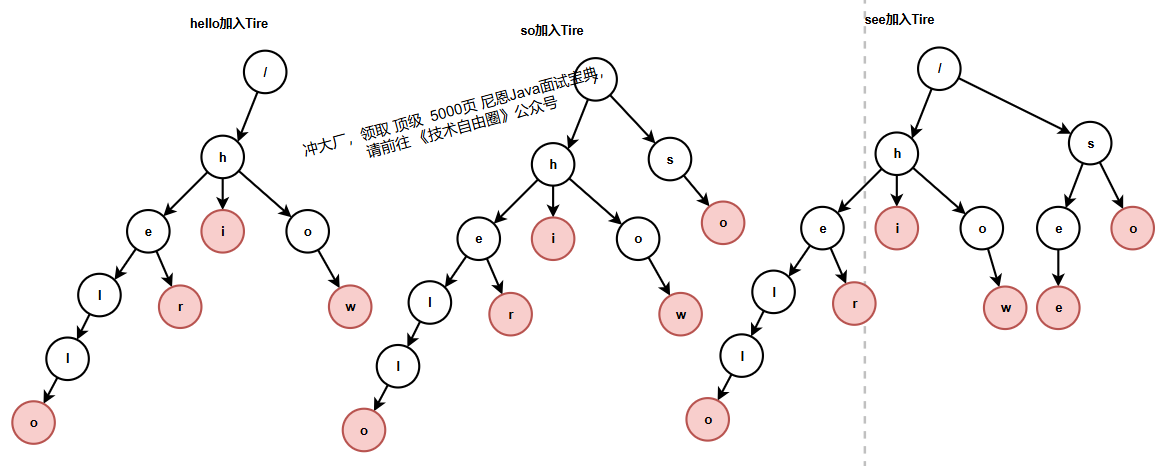
当我们在 Trie 树中查找一个字符串的时候，比如查找字符串“her”，那我们将要查找的字符串分割成单个的字符 h，e，r，然后从 Trie 树的根节点开始匹配。如图所示，绿色的路径就是在 Trie 树中匹配的路径

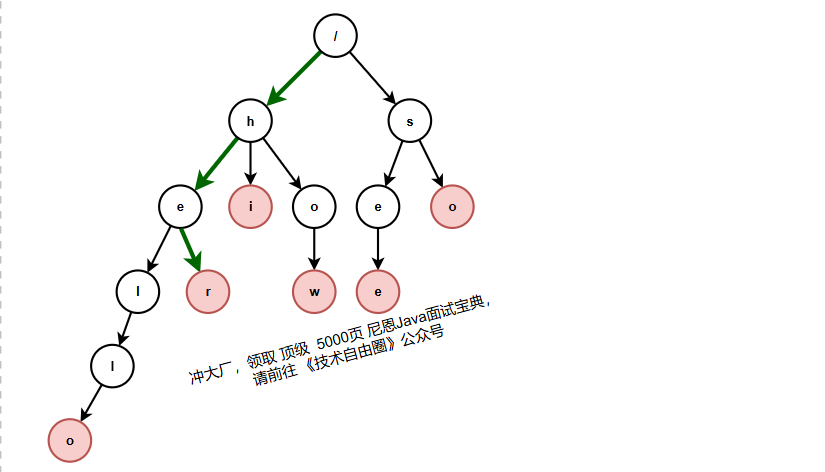
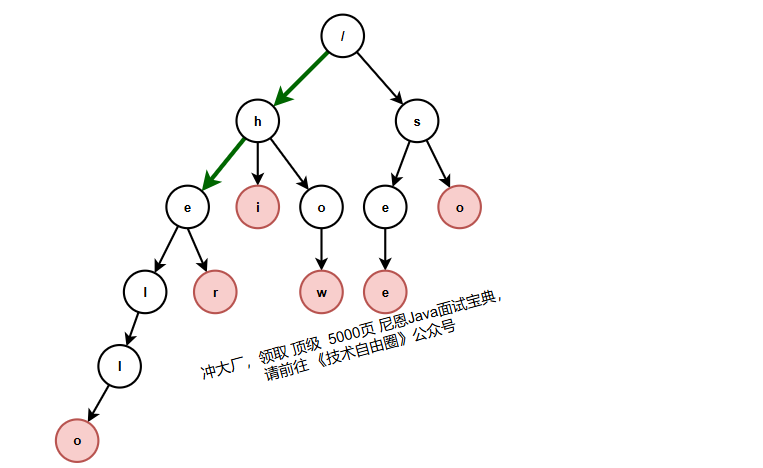
如果我们要查找的是字符串“he”呢？我们还用上面同样的方法，从根节点开始，沿着某条路径来匹配，如图所示，绿色的路径，是字符串“he”匹配的路径。但是，路径的最后一个节点“e”并不是红色的。也就是说，“he”是某个字符串的前缀子串，但并不能完全匹配任何字符串。

Trie树 与 暴力匹配（BF）的对比

相比于暴力匹配（BF）算法，Trie树的优势主要体现在以下方面：

（1）‌时间复杂度优化‌：BF算法每次匹配需完整遍历主串和模式串，时间复杂度为O(n×m)，而Trie树通过前缀共享将查询时间降至O(k)（k为模式串长度），适合高频查询场景（如搜索引擎关键词提示）

（2）‌多模式串处理能力‌：BF需对每个模式串单独匹配，而Trie树可一次性存储所有模式串，实现多模式串的并行匹配（如敏感词过滤），避免重复计算。

（3）‌功能扩展性‌：Trie树天然支持前缀匹配、最长前缀查找等功能，而BF仅支持完整匹配。例如输入法联想提示、路由表最长前缀匹配等场景必须依赖Trie结构。

（4）‌预处理优势‌：Trie树通过预先构建字符路径，牺牲空间换取查询效率，尤其适合静态词库（如字典）；而BF每次匹配均需从头计算，无法复用历史结果。

**BF -> Trie树‌演进本质‌：**Trie树通过空间换时间和结构化存储，解决了BF算法在处理多模式串、前缀匹配时的低效问题，是算法设计从“暴力遍历”到“智能索引”的典型演进。

Trie 树的实现敏感词过滤

Trie 树主要有两个操作

（1）将字符串集合构造成 Trie 树。这个过程分解开来的话，就是一个将字符串插入到 Trie 树的过程。

（2）然后是在 Trie 树中查询一个字符串。

trie树实现敏感词过滤参考代码：

/**
 * 敏感词过滤器核心类，基于Trie树实现高效匹配
 * 特点：支持中文敏感词检测，时间复杂度O(n) 
 */
public class SensitiveWordFilter {
   
   
  
    // Trie树根节点（空节点）
    private final TrieNode root = new TrieNode();
    // 敏感词替换字符串
    private static final String REPLACEMENT = "***";

    /**
     * Trie树节点静态内部类
     * 采用HashMap存储子节点实现动态扩展
     */
    private static class TrieNode {
   
   
        // 子节点映射表 <字符, 对应子节点>
        Map<Character, TrieNode> children = new HashMap<>();
        // 标记当前节点是否为某个敏感词的结尾
        boolean isEnd;
    }

    /**
     * 加载敏感词库构建Trie树
     * @param keywords 敏感词集合
     */
    public void loadKeywords(Set<String> keywords) {
   
   
        for (String word : keywords) {
   
   
            TrieNode node = root; // 从根节点开始构建
            for (int i = 0; i < word.length(); i++) {
   
   
                char c = word.charAt(i);
                // 如果当前字符不存在于子节点，则新建分支
                if (!node.children.containsKey(c)) {
   
   
                    node.children.put(c, new TrieNode());
                }
                // 移动到下一级节点
                node = node.children.get(c);
            }
            // 标记敏感词结束位置
            node.isEnd = true;
        }
    }

    /**
     * 执行敏感词过滤主方法
     * @param text 待过滤文本
     * @return 过滤后的安全文本
     */
    public String filter(String text) {
   
   
        StringBuilder result = new StringBuilder();
        int start = 0; // 文本扫描起始位置
        
        while (start < text.length()) {
   
   
            // 检测从start位置开始的敏感词
            int matchLength = checkSensitiveWord(text, start);
            if (matchLength > 0) {
   
   
                // 存在敏感词则替换
                result.append(REPLACEMENT);
                start += matchLength; // 跳过已检测部分
            } else {
   
   
                // 无敏感词则保留原字符
                result.append(text.charAt(start++));
            }
        }
        return result.toString();
    }

    /**
     * 检查指定位置开始的敏感词
     * @param text 待检测文本
     * @param startIndex 检测起始位置
     * @return 匹配到的敏感词长度（未匹配返回0）
     */
    private int checkSensitiveWord(String text, int startIndex) {
   
   
        TrieNode tempNode = root;
        int matchLength = 0;
        
        for (int i = startIndex; i < text.length()