Day08 字典&标签编码&连续变量处理

字典的相关知识点

字典的创建：

dict1 = {'name': 'Jack', 'age': 18, 'gender': 'male'}
print(dict1)

字典中元素的获取

print(dict1['name'])

字典中元素的增删改

dict1['age'] = 20
dict1['score'] = 90
del dict1['gender']
print(dict1)

标签编码

        离散数据如果不存在顺序，则使用独热编码，函数为pd.get_dummies()，但是同时，有一些离散变量数据存在数据。如data.csv中"Home Ownership"一列，可以根据抵御风险的能力进行标签和赋值。

import pandas as pd
data = pd.read_csv('data.csv')
print(data['Home Ownership'].value_counts())

运行结果为：

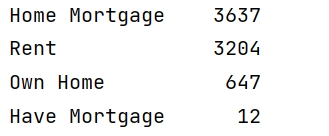
        可以分为4类，第一类是：有房屋贷款，有房子；第二类是：租房子，没有房子；第三类是：有自己的房子；第四类是：有房子，但有其他的贷款。因此，抵御风险的能力可以确定为：

        自有住房 ＜ 租房 ＜ 有其他贷款 ＜ 住房抵押贷款

        因此，可以根据此顺序进行分类，并观察前几行的数据：

mapping = {
    'Rent':0,
    'Own Home':1,
    'Have Mortgage':2,
    'Home Mortgage':3,
}
print(data['Home Ownership'].head())

运行结果为：

按照之前设置的标签进行赋值处理：

data['Home Ownership'] = data['Home Ownership'].map(mapping)
print(data['Home Ownership'].head())

得到的结果为：

如果数据中包含多个离散变量可以分类，可以使用字典的嵌套：

mapping = {
    'Home Ownership': {'Rent':0,
        'Own Home':1,
        'Have Mortgage':2,
        'Home Mortgage':3,},
    'Term':{
        'Short Term': 1,
        'Long Term': 0
    }
}

连续变量处理

        在实际问题中，需要建模处理，并对每一行的数据进行比较分析，此时需要对一列的数据进行归一化。对于归一化，可以手写函数实现，同时也可以使用机器学习中sklearn函数实现。

def manual_normalized(data):
    min_value = data.min()
    max_value = data.max()
    normalized_data = (data - min_value) / (max_value - min_value)
    return normalized_data
data['Annual Income'] = manual_normalized(data['Annual Income'])
print(data['Annual Income'].head())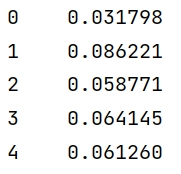

也可以调用sklearn函数实现：

from sklearn.preprocessing import StandardScaler,MinMaxScaler
data = pd.read_csv('data.csv')
min_max_scaler = MinMaxScaler()
data['Annual Income'] = min_max_scaler.fit_transform(data[['Annual Income']])
print(data['Annual Income'].head())

注意：在Scikit-learn中，MinMaxScaler的fit_transform方法要求输入数据是二维数组（形状为(n_samples, n_features)）。当使用data['Annual Income']（单括号）时，返回的是一个一维的Series对象，形状为(n_samples,)，不符合维度要求，会导致报错。

对于标准化，调用StandardScaler函数实现：

data = pd.read_csv('data.csv')
scaler = StandardScaler()
data['Annual Income'] = scaler.fit_transform(data[['Annual Income']])
print(data['Annual Income'].head())

1. 归一化(MinMaxScaler)结果 ：
将数据线性缩放到[0,1]区间
公式：(x - min)/(max - min)
适用场景：数据分布边界明确，不需要考虑异常值
2. 标准化(StandardScaler)结果 ：
将数据转换为均值为0，标准差为1的分布
公式：(x - μ)/σ
适用场景：数据存在异常值或符合正态分布假设

@浙大疏锦行