递归函数的几个典型例子

原创于 2025-01-02 09:08:03 发布 · 1k 阅读

12 ·

CC 4.0 BY-SA版权

文章标签：

#算法

一、什么是递归函数？

递归函数是一个直接或间接调用自身的函数。递归是一种解决问题的编程技术，常用于分治思想和问题的自相似结构。例如，求解数学中的阶乘、斐波那契数列、汉诺塔问题等。

二、递归的基本思想

递归函数在设计时通常包含两个部分：

1、标准情形

定义问题的最简单情形，递归的停止条件。

当满足基本情形时，函数直接返回结果不再递归。

2、递归情形

将问题分解为更小的子问题，通过递归调用自身解决问题。

三、递归的工作原理

1、每一次递归调用会将函数的当前状态压入调用栈。

2、递归进入下一层，直到满足基准情形。

3、从最深的递归层次逐步返回并解决问题。

四、递归函数的实现与示例

1. 求阶乘的递归函数

阶乘的数学定义：n!=n×(n−1)×(n−2)×⋯×1

基准情形：0!=1

递归情形：n!=n×(n−1)!

代码实现：

#include <stdio.h>

int factorial(int n) {
    if (n == 0) {
        return 1;  // 基准情形
    }
    return n * factorial(n - 1);  // 递归情形
}

int main() {
    int num = 5;
    printf("%d! = %d\n", num, factorial(num));
    return 0;
}

执行流程：输入factorial(5)，函数调用链如下：

factorial(5) -> 5 * factorial(4)
factorial(4) -> 4 * factorial(3)
factorial(3) -> 3 * factorial(2)
factorial(2) -> 2 * factorial(1)
factorial(1) -> 1 * factorial(0)
factorial(0) = 1  // 基准情形

逐层返回结果：

factorial(1) = 1
factorial(2) = 2 * 1 = 2
factorial(3) = 3 * 2 = 6
factorial(4) = 4 * 6 = 24
factorial(5) = 5 * 24 = 120

2. 斐波那契数列

斐波那契数列的定义：

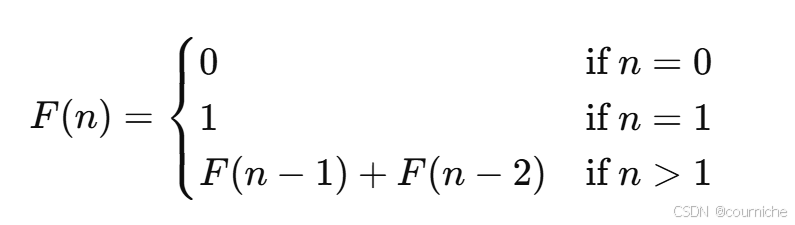
#include <stdio.h>

int fibonacci(int n) {
    if (n == 0) return 0;  // 基准情形
    if (n == 1) return 1;  // 基准情形
    return fibonacci(n - 1) + fibonacci(n - 2);  // 递归情形
}

int main() {
    int n = 10;
    for (int i = 0; i <= n; i++) {
        printf("F(%d) = %d\n", i, fibonacci(i));
    }
    return 0;
}

3. 汉诺塔问题

问题：将 n个盘子从柱子 A 移到柱子 C，中间可以使用柱子 B，且任何时刻较大的盘子不能放在较小的盘子上。

递归思想：

如果只有1个盘子：直接从A移动到C。

如果有n个盘子：

1、将前n-1个盘子从A移动到B

2、将第n个盘子从A移动到C

3、再将n-1个盘子从B移动到C

void hanoi(int n, char from, char to, char aux) {
    if (n == 1) {
        printf("Move disk 1 from %c to %c\n", from, to);
        return;
    }
    hanoi(n - 1, from, aux, to);
    printf("Move disk %d from %c to %c\n", n, from, to);
    hanoi(n - 1, aux, to, from);
}

4. 字符串反转

问题：使用递归反转字符串。

递归思想：

将字符串分为首字符和剩余部分

反转剩余部分，再加上首字符

void reverse(char *str, int start, int end) {
    if (start >= end) {
        return; // 基准条件
    }
    char temp = str[start];
    str[start] = str[end];
    str[end] = temp;
    reverse(str, start + 1, end - 1); // 递归调用
}