【元旦福利大放送】最小生成树规范课设源代码全套详解

数据结构课程设计

设计要求

  从文件中读取一个交通网络图，图中包含若干城市间的距离信息，设计程序分别以每个城市为起点，建立最小生成树并输出，并计算得到的最小生成树的代价。要求:

• 交通图自己设计，至少要包含 20 个城市，40 条边，城市用实际的城市命名。
• 以邻接矩阵为存储结构分别用 prim 算法和 kruskal 算法实现上述操作
• 以邻接表为存储结构分别用 prim 算法和 kruskal 算法实现上述操作
• 最小生成树的输出格式为:
  第1条边郑州–>武汉 500 公里
  第2条边武汉–>长沙 630 公里
  …

相关概念

最小生成树

  一个有 n 个结点的连通图的生成树是原图的极小连通子图，且包含原图中的所有 n 个结点，并且有保持图连通的最少的边。 最小生成树可以用kruskal（克鲁斯卡尔）算法或prim（普里姆）算法求出。即最小权重生成树。

Prim

  设有初始顶点集合V，初始边集合E

1. 从连通图G的顶点中任意选择一个点加入集合V
2. 在与V集合有关的边中，寻找最小权值且含有一个集合外顶点的边，将新顶点加入V
3. 重复2操作直至V包含连通图G中的所有顶点

Kruskal

  设有初始顶点集合V，初始边集合E

1. 遍历集合E中的边，每次取最小权值且含有一个集合外顶点的边，将新顶点加入V
2. 重复1操作直至V包含连通图G中的所有顶点

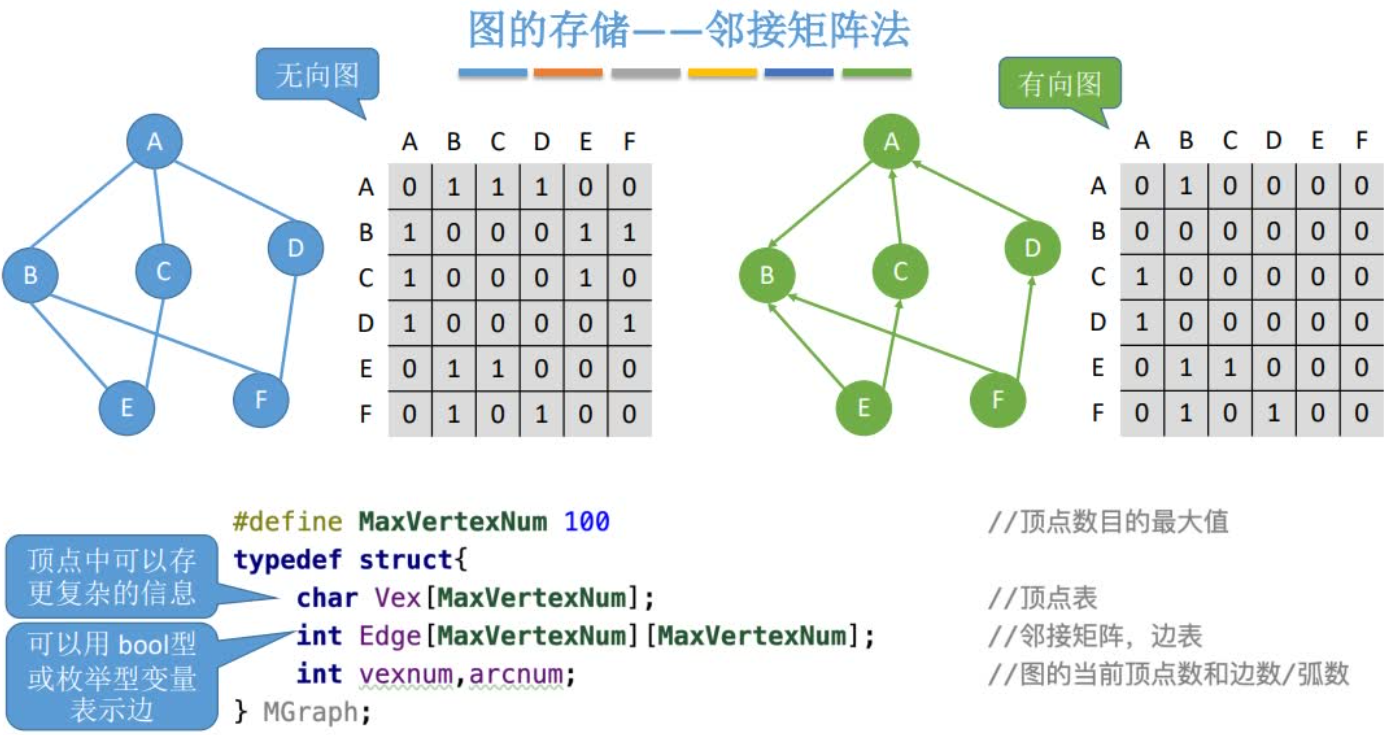
邻接矩阵

  邻接矩阵是以数组的形式实现图的储存的

1. 直观、简单、好理解
2. 方便检查任意一对定点间是否存在边
3. 方便找任一顶点的所有“邻接点”（有边直接相连的顶点）
4. 方便计算任一顶点的度

  邻接矩阵的局限性：时间复杂度 $O(n^2)$，空间复杂度 $O(n^2)$

1. 浪费空间。对于稠密图还是很合算的，但是对于稀疏图（点很多而边很少）有大量无效元素。
2. 浪费时间。要确定图中有多少条边，则必须按行、按列对每个元素进行检测，所花费的时间代价很大。

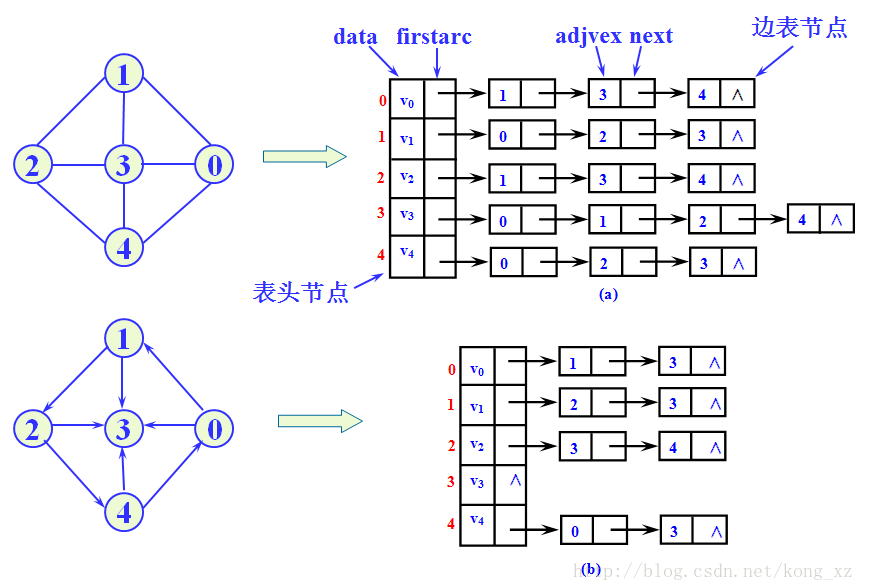
邻接表

  图的邻接表存储方法是一种顺序分配与链式分配相结合的存储方法

  在邻接表中，对图中每个顶点建立一个单链表，第i个单链表中的节点表示依附于顶点i的边（对有向图是以顶点i为尾的边），每个单链表上附设一个表头节点

  邻接表特点

1. 邻接表表示不唯一。这是因为在每个顶点对应的单链表中，各边节点的链接次序可以是任意的，取决于建立邻接表的算法以及边的输入次序
2. 对于有 n 个顶点和 e 条边的无向图，其邻接表有 n 个顶点节点和 2e 个边节点。显然，在总的边数小于 n(n-1)/2 的情况下，邻接表比邻接矩阵要节省空间
3. 对于无向图，邻接表的顶点 i 对应的第i个链表的边节点数目正好是顶点i的度
4. 对于有向图，邻接表的顶点 i 对应的第i个链表的边节点数目仅仅是顶点i的出度。其入度为邻接表中所有 adjvex 域值为i的边节点数目

功能模块

路径读取及预处理

  头文件函数

#include <fstream>//文件流函数读取文件内容 
#include <vector>//作为数据缓存数组 
#include <map>//对城市名进行一一映射
#include <set>//对城市名进行去重 

  全局变量

//全局变量列表如下： 
//读取文件及数据预处理
vector<string> arr;//缓存数组  
struct Edge//边定义：起点 终点 边权 
{
	int a,b,c;
};
vector<Edge> edge;//边数组 
map<string,int> Q_to_num;//完成城市序号映射 
map<int,string> Q_to_name;//完成城市序号映射 
set<string> cities;//完成城市去重 

  测试数据如下，含有一个"桂林 -> 广州"的重边，总城市 20，总边数 40，有效边数 39：

兰州 西安 626	
兰州 成都 865
成都 重庆 302
大理 成都 872
西安 成都 742	
西安 重庆 757
西安 郑州 480	
大理 重庆 1106	
大理 昆明 330	
大理 江城 802	
重庆 郑州 1170	
重庆 昆明 831	
重庆 武汉 876	
昆明 江城 406	
昆明 贵阳 515
贵阳 江城 900	
贵阳 长沙 778	
贵阳 桂林 466	
贵阳 南昌 1113	
郑州 贵阳 1410
郑州 武汉 510
郑州 南京 658
武汉 长沙 332	
武汉 南昌 345	
武汉 杭州 722	
武汉 南京 531
南京 上海 297	
上海 杭州 170	
杭州 南昌 523	
杭州 香港 1335	
长沙 桂林 515	
长沙 广州 669	
长沙 南昌 337	
南昌 广州 782	
桂林 广州 478	
桂林 南宁 376	
桂林 广州 478	
广州 香港 185
广州 澳门 136	
香港 澳门 225

  将以上数据保存为”地图详情.txt“，路径和code.cpp保持在同一文件夹下。

  使用文件流函数ifstream打开”地图详情.txt“文件，使用cin按照逐个字符串读取，并存入缓冲数组当中。

ifstream f;//设置文件流 
f.open("地图详情.txt",ios::in);//读取文件内容 
string t;
while(f >> t)//以字符串方式读取 
{
	arr.push_back(t);//存入缓冲数组 
}

  在缓冲数组中，以 3 个数据为一组，每组首元素下标对 3 取余为 0，次元素下标对 3 取余为 1，末元素下标对 3 取余为 2，进行路径展示：

//通过缓冲数组完成路径存储 
	printf("_______________________________________________________________________________\n");
	printf("|                      地图信息路径如下，共%d条路径：                         |\n",int(arr.size()) / 3);
	for(int i = 0;i < int(arr.size());i ++ )//3个一组，使用取模滚动 
	{
		if(i % 3 == 0)//起点 
		{
			cout << "|                   " << arr[i] << " ------> ";
			cities.insert(arr[i]);
		}
		else if(i % 3 == 1)//终点 
		{
			cout << arr[i] << " 路径长度为： ";
			cities.insert(arr[i]);
		}
		else if(i % 3 == 2)//路径长度 
		{
			printf("%4d                       |\n",stoi(arr[i]));
		}
	}
	cout << "|_____________________________________________________________________________|" << endl;
	cout << endl << endl << endl;

  由于城市为汉字，使用字符串存储可能乱码，故记得将”地图详情.txt“编码格式调整为ANSI

  对于所有的城市使用set容器进行去重

  每个城市要对应唯一序列号，通过唯一序列号又可查找该城市名称，使用哈希表完成映射和反映射

//完成城市对应序号映射 
	int idx = 0;//城市对应序号初始化 
	printf("_______________________________________________________________________________\n");
	printf("|           去重处理后，城市对应序列依次如下所示，共%d座城市：                |\n",int(cities.size()));
	for(auto t : cities)
	{
		idx ++ ;
		Q_to_num[t] = idx;//对城市->序号实现映射 
		Q_to_name[idx] = t;//对序号->城市实现映射 
		cout << "|                        " << t << " 对应序号为：";
		printf("%5d                               |\n",Q_to_num[t]);
	}
	cout << "|_____________________________________________________________________________|" << endl;
	cout << endl << endl << endl;

  对于数据所给出的边，需要进行重边处理，首先将预处理数组中的所有边按照Edge的格式存入edge数组中

for(int i = 0;i < int(arr.size());i += 3)//以三个为一组，存入edge数组当中 
	{
	
		int a = Q_to_num[arr[i]];//起点信息 
		int b = Q_to_num[arr[i + 1]];//终点信息 
		int c = stoi(arr[i + 2]);//路径长度 
		edge.push_back({a,b,c}); 
	} 

  对 edge 数组中的元素进行边权升序排列，排列后边权相同的边将会相邻。定义临时数组 temp，暂存 edge 中双指针筛下的唯一边，而后将 edge 数组更新

sort(edge.begin(),edge.end(),cmp);//边权升序排序，方便去重 
	vector<Edge> temp;//临时数组定义 
n for(int i = 0;i < int(edge.size());i ++ )//双指针对重复元素进行去重 
	{
		int j = i + 1;
		while(j < int(edge.size()) && edge[j].a == edge[i].a && edge[j].b == edge[i].b && edge[j].c == edge[i].c)j ++ ;
		temp.push_back(edge[i]);
		i = j - 1;
	}
	edge = temp;//去重后，更新edge数组 

  展示有效边

cout << "经检测，存在"<< int(arr.size()) / 3 - int(edge.size()) << "条重边" << endl;
	printf("_______________________________________________________________________________\n");
	printf("                      地图信息路径如下，共%d条有效路径：                       \n",int(edge.size()));
	for(int i = 0;i < int(edge.size());i ++ )
	{
		cout << "                    " << Q_to_name[edge[i].a] << " ------> ";
		cout << Q_to_name[edge[i].b] << " 路径长度为： ";
		printf("%4d                        \n",edge[i].c);
	}
	cout << "_____________________________________________________________________________\n" << endl;
	cout << endl << endl << endl;

  关闭文件流

f.close();//关闭文件 

以邻接矩阵为存储结构的Prim实现

  全局变量定义

const int M = 2020,INF = 0x3f3f3f3f;
int dis[M];
bool st[M];
int g[M][M];
int pre[M];

  将edge中的数据导入邻接矩阵

//初始化+数据导入 
	memset(g,0x3f,sizeof(g));//初始化邻接矩阵 
	for(int i = 0;i < int(edge.size());i ++ )
	{
		int a = edge[i].a;
		int b = edge[i].b;
		int c = edge[i].c;
		g[a][b] = g[b][a] = min(g[a][b],c);//对称存储 
	} 

  邻接矩阵的展示

//邻接矩阵展示
	cout << "———————————————————————————————————————" << endl;
	printf("                          地图信息邻接矩阵如下：                               \n");
	cout << "———————————————————————————————————————"<< endl;
	for(int i = 1;i <= int(cities.size());i ++ )
	{
		for(int j = 1;j <= int(cities.size());j ++ )
		{
			if(g[i][j] != INF)printf("%d ",g[i][j]);
			else cout << "INF ";
		}
		cout << endl;
	} 
	cout << "———————————————————————————————————————"<< endl; 
	cout << endl << endl << endl;

  Prim的实现

cout << "选择路径及总cost如下所示：" << endl << endl;
	cout << "———————————————————————————————————————" << endl;
	int ans = 0;//初始化cost 
    memset(dis,0x3f,sizeof(dis));//初始化dist数组 
    memset(st,false,sizeof(st));//初始化st数组 
    memset(pre,-1,sizeof(pre));//初始化pre数组 
    dis[1] = 0;//默认将第一个边加入集合当中 
    for(int i = 0;i < int(cities.size());i ++ )//遍历头结点 
    {
        int t = -1;
        for(int j = 1;j <= int(cities.size());j ++ )//找到与集合相距距离最短的点 
        {
            if((!st[j]) && (t == -1 || dis[t] > dis[j]))t = j;
        }
        if(i > 0)
        {
        	cout << "         第" << i << "次选择路径为："<< Q_to_name[pre[t]] << " -> " << Q_to_name[t] << " 长度为：" << g[pre[t]][t] << endl; 
            ans += g[pre[t]][t];//cost累加 
        }
        st[t] = true;//将结点t加入集合 
        for (int j = 1; j <= int(cities.size());j ++ )//更新 
        {  
            if (!st[j] && g[t][j] != 0 && g[t][j] < dis[j])//更新其他点到集合的最短距离 
            {  
                dis[j] = g[t][j];  
                pre[j] = t; // 更新j的前驱节点为t  
            }  
        }  
    }
    printf("\n         最小生成树代价为：%d\n",ans);
    cout << "———————————————————————————————————————" << endl;

以邻接表为存储结构的Prim实现

  全局变量定义

const int N = 1e6 + 10;
int e[N], ne[N], w[N], h[N], idx;
int n, m;
int vis[N];
int dist[N];
//邻接表加边函数 
void add(int a, int b, int c) 
{
	e[idx] = b;
	w[idx] = c;
	ne[idx] = h[a];
	h[a] = idx ++ ;
} 

  邻接表的初始化

//初始化+数据导入 
memset(h, -1, sizeof(h));//头结点初始化为-1 
idx = 0;//节点初始化 
for(int i = 0;i < int(edge.size());i ++ )
{
	//读取边内容，构造邻接表 
	int a = edge[i].a;
	int b = edge[i].b;
	int c = edge[i].c;
	//无向图加两次边 
	add(a,b,c);
	add(b,a,c);
} 

  路径的展示

//路径展示 
	cout << "———————————————————————————————————————" << endl;
	printf("                       地图信息路径如下，共%d条路径：                          \n",int(edge.size()));
	cout << "———————————————————————————————————————"<< endl;
	for(int i = 1;i <= int(cities.size());i ++ )//遍历头结点 
	{
		cout << "            " << Q_to_name[i] << " : ";
		for(int j = h[i];j != -1;j = ne[j])//遍历边界点 
		{
			if(j == h[i])cout << Q_to_name[e[j]];
			else cout << " -> " << Q_to_name[e[j]];
		}
		cout << endl;
	}
	cout << "———————————————————————————————————————"<< endl;
	cout << endl << endl << endl;

  Prim的实现

cout << "选择路径及总cost如下所示：" << endl << endl;
	cout << "———————————————————————————————————————" << endl;
	memset(dist, 0x3f, sizeof(dist));//初始化dist数组 
	dist[1] = 0;//默认首选第一个点，将第一个点加入集合 
	int ans = 0;//初始化总cost 
	for (int i = 0; i < int(edge.size());i ++ )//遍历头结点 
	{
		int t = -1;
		for (int j = 1; j <= int(edge.size());j ++ )//遍历边节点，每次找到距集合最近的点
		{
			if (vis[j])continue;//如果已存在集合，则跳过 
			else if (t < 0 || dist[j] < dist[t])t = j; 
		}
		//输出选择路径 
		for (int k = h[t]; k != -1; k = ne[k])//遍历新加入节点的所有临边 
		{
			int j = e[k];
			if (vis[j] && w[k] == dist[t])//找到与加入边权相同的那条边 
			{
				cout << "         第" << i << "次选择路径为："<< Q_to_name[j] << " -> " << Q_to_name[t] << " 长度为：" << w[k] << endl;//输出路径 
				ans += dist[t];//cost累加 
				break;
			}
		}
		for(int k = h[t]; k != -1; k = ne[k])dist[e[k]] = min(dist[e[k]], w[k]); //更新其他点到集合的最短路径 
		vis[t] = 1;//将该点加入集合 
	}
	cout << endl << "         最小代价为：" << ans << endl;
	cout << "———————————————————————————————————————" << endl;

以邻接矩阵为存储结构的Kruskal实现

  全局变量定义

int dis[M];
bool st[M];
int g[M][M];
int pre[M];
int p[N]; 
int find(int x)
{
	if(p[x] != x)p[x] = find(p[x]);
	return p[x];
}
int cmp(Edge a,Edge b)
{
	return a.c < b.c;
}

  Kruskal 算法的重点不在于使用何种处理方式，而是在于如何读取边信息，对边集合进行操作

  从邻接矩阵中读取边信息

//初始化+数据导入 
	memset(g,INF,sizeof(g));//初始化邻接矩阵 
	for(int i = 0;i < int(edge.size());i ++ )
	{
		int a = edge[i].a;
		int b = edge[i].b;
		int c = edge[i].c;
		g[a][b] = g[b][a] = min(g[a][b],c);//对称存储 
	} 

  邻接矩阵展示

//邻接矩阵展示
	cout << "———————————————————————————————————————" << endl;
	printf("                          地图信息邻接矩阵如下：                               \n");
	cout << "———————————————————————————————————————"<< endl;
	for(int i = 1;i <= int(cities.size());i ++ )
	{
		for(int j = 1;j <= int(cities.size());j ++ )
		{
			if(g[i][j] != INF)//若两点之间存在边 
			{
				printf("%d ",g[i][j]);//输出 
			}
			else cout << "INF ";//否则输出INF，表示无边 
		}
		cout << endl;
	} 
	cout << "———————————————————————————————————————"<< endl; 
	cout << endl << endl << endl;

  读取邻接矩阵获得边信息

//读取邻接矩阵获取边信息 
	vector<Edge> o; 
	//无向图边的存储为对称矩阵，对边信息进行提取只需对上三角或下三角矩阵进行遍历即可，在这里遍历下三角矩阵 
	for(int i = 1;i <= int(cities.size());i ++ )
	{
		for(int j = 1;j <= i;j ++ )
		{
			if(g[i][j] != INF)//若两点之间存在边 
			{
				o.push_back({j,i,g[i][j]});//则存入 
			}
		}
	} 

  设置动态数组 o，用于存 Edge 边类型，对 o 进行边权值升序排序，数据保证必然存在最小生成树，故进行 n - 1 条边的选取，也就是进行 n - 1 次顶点集合的操作，操作之后，集合中的点的数量包含连通图 G 中的所有点

//Kruskal + 并查集 + 排序(小根堆) 
	cout << "选择路径及总cost如下所示：" << endl << endl;
	cout << "———————————————————————————————————————" << endl;
	printf("       共%d个有效地点，故进行%d条边的选择：\n",int(cities.size()),int(cities.size()) - 1);
	sort(o.begin(),o.end(),cmp);//边按权值升序排序，依次取较小边权进行操作 
	for(int i = 1;i <= int(cities.size());i ++ )p[i] = i;//初始化并查集数组 
	int ans = 0,idx = 0;//对应总cost 路径选择次序 
	for(int i = 0;i < int(edge.size());i ++ )//依次遍历边 
	{
		int a = edge[i].a;
        int b = edge[i].b;
        int c = edge[i].c;
        a = find(a);
        b = find(b);
        //若该边所在点未在集合之中 
        if(find(a) != find(b))
        {
            p[find(a)] = find(b);//加入集合 
            ans += c;//cost累加 
            printf("       第%d次选择的路径为：",++ idx);
            cout << Q_to_name[a] << " -> " << Q_to_name[b] << " 路径长度为：" << c << endl;
        }
	}
	cout << endl << "       最小生成树代价为：" << ans << endl; 
	cout << "———————————————————————————————————————" << endl;

以邻接表为存储结构的Kruskal实现

  全局变量定义

const int N = 1e6 + 10;
int e[N], ne[N], w[N], h[N], idx;
int n, m;
int vis[N];
int dist[N];
int find(int x)
{
	if(p[x] != x)p[x] = find(p[x]);
	return p[x];
}
int cmp(Edge a,Edge b)
{
	return a.c < b.c;
}

  Kruskal 算法的重点不在于使用何种处理方式，而是在于如何读取边信息，对边集合进行操作

  从邻接表中读取边信息

//初始化+数据导入 
	memset(h, -1, sizeof(h));//头结点初始化为-1 
	idx = 0;//节点初始化 
	for(int i = 0;i < int(edge.size());i ++ )
	{
		//读取边内容，构造邻接表 
		int a = edge[i].a;
		int b = edge[i].b;
		int c = edge[i].c;
		//无向图加两次边 
		add(a,b,c);
		add(b,a,c);
	} 

  邻接表展示

//路径展示 
	cout << "———————————————————————————————————————" << endl;
	printf("                       地图信息路径如下，共%d条路径：                          \n",int(edge.size()));
	cout << "———————————————————————————————————————"<< endl;
	for(int i = 1;i <= int(cities.size());i ++ )//遍历头结点 
	{
		cout << "            " << Q_to_name[i] << " : ";
		for(int j = h[i];j != -1;j = ne[j])//遍历边界点 
		{
			if(j == h[i])cout << Q_to_name[e[j]];
			else cout << " -> " << Q_to_name[e[j]];
		}
		cout << endl;
	}
	cout << "———————————————————————————————————————"<< endl;
	cout << endl << endl << endl;

  读取邻接表获取边信息

//读取邻接表获取边信息 
	vector<Edge> o; //定义临时数组o，用于从邻接表中读取信息 
	for(int i = 1;i <= int(cities.size());i ++ )//遍历头结点 
	{
		for(int j = h[i];j != -1;j = ne[j])//遍历边节点 
		{
			o.push_back({i,e[j],w[j]});//i为头结点编号，e[j]为边节点编号，w[j]为 i -> e[j] 边的权值 
		}
	} 

  设置动态数组 o，用于存 Edge 边类型，对 o 进行边权值升序排序，数据保证必然存在最小生成树，故进行 n - 1 条边的选取，也就是进行 n - 1 次顶点集合的操作，操作之后，集合中的点的数量包含连通图 G 中的所有点

//Kruskal + 并查集 + 排序(小根堆) 
	cout << "选择路径及总cost如下所示：" << endl << endl;
	cout << "———————————————————————————————————————" << endl;
	printf("       共%d个有效地点，故进行%d条边的选择：\n",int(cities.size()),int(cities.size()) - 1);
	sort(o.begin(),o.end(),cmp);//边按权值升序排序，依次取较小边权进行操作 
	for(int i = 1;i <= int(cities.size());i ++ )p[i] = i;//初始化并查集数组 
	int ans = 0,idx = 0;//对应总cost 路径选择次序 
	for(int i = 0;i < int(edge.size());i ++ )//依次遍历边 
	{
		int a = edge[i].a;
        int b = edge[i].b;
        int c = edge[i].c;
        a = find(a);
        b = find(b);
        //若该边所在点未在集合之中 
        if(find(a) != find(b))
        {
            p[find(a)] = find(b);//加入集合 
            ans += c;//cost累加 
            printf("       第%d次选择的路径为：",++ idx);
            cout << Q_to_name[a] << " -> " << Q_to_name[b] << " 路径长度为：" << c << endl;
        }
	}
	cout << endl << "       最小生成树代价为：" << ans << endl; 
	cout << "———————————————————————————————————————" << endl;

菜单

void display()
{
	cout << "_______________________________________________________________________________" << endl;
	cout << "|                             最小生成树问题                                  |" << endl;
	cout << "|-----------------------------------------------------------------------------|" << endl;
	cout << "|                       1.路径读取及预处理                                    |" << endl;
	cout << "|-----------------------------------------------------------------------------|" << endl;
	cout << "|                       2.以邻接矩阵为存储结构的Prim实现                      |" << endl;
	cout << "|-----------------------------------------------------------------------------|" << endl;
	cout << "|                       3.以邻接表为存储结构的Prim实现                        |" << endl;
	cout << "|-----------------------------------------------------------------------------|" << endl;
	cout << "|                       4.以邻接矩阵为存储结构的Kruskal实现                   |" << endl;
	cout << "|-----------------------------------------------------------------------------|" << endl;
	cout << "|                       5.以邻接表为存储结构的Kruskal实现                     |" << endl;
	cout << "|-----------------------------------------------------------------------------|" << endl;
	cout << "|                       6.退出                                                |" << endl;
	cout << "|_____________________________________________________________________________|" << endl;
	cout << endl; cout << endl; cout << endl; 
} 

main函数

int flag = INF;//菜单标识符 
    while(flag != 666)
    {
    	system("cls");//清空程序框内容
		display();//展示菜单 
		printf("请选择您想要实现的功能序号：");
		scanf("%d",&flag);
		switch(flag)//匹配功能 
		{
			case 1:
				system("cls");//清空程序框内容
				read();//读取文件内容及处理 
				cout << "路径读取已完成！！！请输入-1返回：";
				cin >> flag;
				if(flag == -1)continue;
				break;
			case 2:
				system("cls");//清空程序框内容
				init_Prim1();//以邻接矩阵为存储结构 Prim 
				cout << "请输入-1返回："; 
				cin >> flag;
				if(flag == -1)continue;
				break;
			case 3:
				system("cls");//清空程序框内容
				init_Prim2();//以邻接表为存储结构 Prim 
				cout << "请输入-1返回："; 
				cin >> flag;
				if(flag == -1)continue;
				break;
			case 4:
				system("cls");//清空程序框内容
				init_Kruskal1();//以邻接矩阵为存储结构 Kruskal 
				cout << "请输入-1返回："; 
				cin >> flag;
				if(flag == -1)continue;
				break;
			case 5:
				system("cls");//清空程序框内容
				init_Kruskal2();//以邻接表为存储结构 Kruskal
				cout << "请输入-1返回："; 
				cin >> flag;
				if(flag == -1)continue;
				break;
			case 6:
				system("cls");//清空程序框内容
				printf(
				    "                ********\n"
				    "               ************\n"
				    "               ####....#.\n"
				    "             #..###.....##....\n"
				    "             ###.......######              ###            ###\n"
				    "                ...........               #...#          #...#\n"
				    "               ##*#######                 #.#.#          #.#.#\n"
				    "            ####*******######             #.#.#          #.#.#\n"
				    "           ...#***.****.*###....          #...#          #...#\n"
				    "           ....**********##.....           ###            ###\n"
				    "           ....****    *****....\n"
				    "             ####        ####\n"
				    "           ######        ######\n"
				    "##############################################################\n"
				    "#...#......#.##...#......#.##...#......#.##------------------#\n"
				    "###########################################------------------#\n"
				    "#..#....#....##..#....#....##..#....#....#####################\n"
				    "##########################################    #----------#\n"
				    "#.....#......##.....#......##.....#......#    #----------#\n"
				    "##########################################    #----------#\n"
				    "#.#..#....#..##.#..#....#..##.#..#....#..#    #----------#\n"
				    "##########################################    ############\n"
				    );
				cout << "谢谢您的使用！再见！！！" << endl; 
				flag = 666;
				break;
		} 
	}

配置文件

头文件

#include <iostream>
#include <fstream>//文件流函数读取文件内容 
#include <vector>//作为数据缓存数组 
#include <map>//对城市名进行一一映射
#include <set>//对城市名进行去重 
#include <cstring>//memset重置数组 
#include <algorithm>//用于sort+cmp自定义排序 

全局变量

//全局变量列表如下： 
//读取文件及数据预处理
vector<string> arr;//缓存数组  
struct Edge//边定义：起点 终点 边权 
{
	int a,b,c;
};
vector<Edge> edge;//边数组 
map<string,int> Q_to_num;//完成城市序号映射 
map<int,string> Q_to_name;//完成城市序号映射 
set<string> cities;//完成城市去重 
//邻接矩阵
const int M = 2020,INF = 0x3f3f3f3f;
int dis[M];
bool st[M];
int g[M][M];
int pre[M];
//邻接表
const int N = 1e6 + 10;
int e[N], ne[N], w[N], h[N], idx;
int n, m;
int vis[N];
int dist[N];
//邻接表加边函数 
void add(int a, int b, int c) 
{
	e[idx] = b;
	w[idx] = c;
	ne[idx] = h[a];
	h[a] = idx ++ ;
} 
//并查集 
int p[N]; 
int find(int x)
{
	if(p[x] != x)p[x] = find(p[x]);
	return p[x];
}
//sort 
int cmp(Edge a,Edge b)
{
	return a.c < b.c;
}

函数列表

//函数列表如下:
void add(int a, int b, int c); //邻接表加边函数 
int find(int x); //并查集找爹函数+路径压缩 
int cmp(Edge a,Edge b); //重定向sort函数实现边权升序排序 
void display(); //菜单函数 
void read(); //路径读取及预处理功能 
void init_Prim1(); //以邻接矩阵为存储结构的Prim实现
void init_Prim2(); //以邻接表为存储结构的Prim实现
void init_Kruskal1(); //以邻接矩阵为存储结构的Kruskal实现
void init_Kruskal2(); //以邻接表为存储结构的Kruskal实现

源代码

#include <iostream>
#include <fstream>//文件流函数读取文件内容 
#include <vector>//作为数据缓存数组 
#include <map>//对城市名进行一一映射
#include <set>//对城市名进行去重 
#include <cstring>//memset重置数组 
#include <algorithm>//用于sort+cmp自定义排序 
using namespace std;
//全局变量列表如下： 
//读取文件及数据预处理
vector<string> arr;//缓存数组  
struct Edge//边定义：起点 终点 边权 
{
	int a,b,c;
};
vector<Edge> edge;//边数组 
map<string,int> Q_to_num;//完成城市序号映射 
map<int,string> Q_to_name;//完成城市序号映射 
set<string> cities;//完成城市去重 
//邻接矩阵
const int M = 2020,INF = 0x3f3f3f3f;
int dis[M];
bool st[M];
int g[M][M];
int pre[M];
//邻接表
const int N = 1e6 + 10;
int e[N], ne[N], w[N], h[N], idx;
int n, m;
int vis[N];
int dist[N];
//邻接表加边函数 
void add(int a, int b, int c) 
{
	e[idx] = b;
	w[idx] = c;
	ne[idx] = h[a];
	h[a] = idx ++ ;
} 
//并查集 
int p[N]; 
int find(int x)
{
	if(p[x] != x)p[x] = find(p[x]);
	return p[x];
}
//sort 
int cmp(Edge a,Edge b)
{
	return a.c < b.c;
}
//函数列表如下:
void add(int a, int b, int c); //邻接表加边函数 
int find(int x); //并查集找爹函数+路径压缩 
int cmp(Edge a,Edge b); //重定向sort函数实现边权升序排序 
void display(); //菜单函数 
void read(); //路径读取及预处理功能 
void init_Prim1(); //以邻接矩阵为存储结构的Prim实现
void init_Prim2(); //以邻接表为存储结构的Prim实现
void init_Kruskal1(); //以邻接矩阵为存储结构的Kruskal实现
void init_Kruskal2(); //以邻接表为存储结构的Kruskal实现

void display()
{
	cout << "_______________________________________________________________________________" << endl;
	cout << "|                             最小生成树问题                                  |" << endl;
	cout << "|-----------------------------------------------------------------------------|" << endl;
	cout << "|                       1.路径读取及预处理                                    |" << endl;
	cout << "|-----------------------------------------------------------------------------|" << endl;
	cout << "|                       2.以邻接矩阵为存储结构的Prim实现                      |" << endl;
	cout << "|-----------------------------------------------------------------------------|" << endl;
	cout << "|                       3.以邻接表为存储结构的Prim实现                        |" << endl;
	cout << "|-----------------------------------------------------------------------------|" << endl;
	cout << "|                       4.以邻接矩阵为存储结构的Kruskal实现                   |" << endl;
	cout << "|-----------------------------------------------------------------------------|" << endl;
	cout << "|                       5.以邻接表为存储结构的Kruskal实现                     |" << endl;
	cout << "|-----------------------------------------------------------------------------|" << endl;
	cout << "|                       6.退出                                                |" << endl;
	cout << "|_____________________________________________________________________________|" << endl;
	cout << endl; cout << endl; cout << endl; 
} 
void read()
{
	//文件打开 
	ifstream f;//设置文件流 
	f.open("地图详情.txt",ios::in);//读取文件内容 
	string t;
	while(f >> t)//以字符串方式读取 
	{
		arr.push_back(t);//存入缓冲数组 
	}
	
	//通过缓冲数组完成路径存储 
	printf("_______________________________________________________________________________\n");
	printf("|                      地图信息路径如下，共%d条路径：                         |\n",int(arr.size()) / 3);
	for(int i = 0;i < int(arr.size());i ++ )//3个一组，使用取模滚动 
	{
		if(i % 3 == 0)//起点 
		{
			cout << "|                   " << arr[i] << " ------> ";
			cities.insert(arr[i]);
		}
		else if(i % 3 == 1)//终点 
		{
			cout << arr[i] << " 路径长度为： ";
			cities.insert(arr[i]);
		}
		else if(i % 3 == 2)//路径长度 
		{
			printf("%4d                       |\n",stoi(arr[i]));
		}
	}
	cout << "|_____________________________________________________________________________|" << endl;
	cout << endl << endl << endl;
	
	//完成城市对应序号映射 
	int idx = 0;//城市对应序号初始化 
	printf("_______________________________________________________________________________\n");
	printf("|           去重处理后，城市对应序列依次如下所示，共%d座城市：                |\n",int(cities.size()));
	for(auto t : cities)
	{
		idx ++ ;
		Q_to_num[t] = idx;//对城市->序号实现映射 
		Q_to_name[idx] = t;//对序号->城市实现映射 
		cout << "|                        " << t << " 对应序号为：";
		printf("%5d                               |\n",Q_to_num[t]);
	}
	cout << "|_____________________________________________________________________________|" << endl;
	cout << endl << endl << endl;
	
	//重边处理 
	for(int i = 0;i < int(arr.size());i += 3)//以三个为一组，存入edge数组当中 
	{
	
		int a = Q_to_num[arr[i]];//起点信息 
		int b = Q_to_num[arr[i + 1]];//终点信息 
		int c = stoi(arr[i + 2]);//路径长度 
		edge.push_back({a,b,c}); 
	} 
	sort(edge.begin(),edge.end(),cmp);//边权升序排序，方便去重 
	vector<Edge> temp;//临时数组定义 
	for(int i = 0;i < int(edge.size());i ++ )//双指针对重复元素进行去重 
	{
		int j = i + 1;
		while(j < int(edge.size()) && edge[j].a == edge[i].a && edge[j].b == edge[i].b && edge[j].c == edge[i].c)j ++ ;
		temp.push_back(edge[i]);
		i = j - 1;
	}
	edge = temp;//去重后，更新edge数组 
	cout << "经检测，存在"<< int(arr.size()) / 3 - int(edge.size()) << "条重边" << endl;
	printf("_______________________________________________________________________________\n");
	printf("                      地图信息路径如下，共%d条有效路径：                       \n",int(edge.size()));
	for(int i = 0;i < int(edge.size());i ++ )
	{
		cout << "                    " << Q_to_name[edge[i].a] << " ------> ";
		cout << Q_to_name[edge[i].b] << " 路径长度为： ";
		printf("%4d                        \n",edge[i].c);
	}
	cout << "_____________________________________________________________________________\n" << endl;
	cout << endl << endl << endl;
	
	f.close();//关闭文件 
}
void init_Prim1()
{
	//初始化+数据导入 
	memset(g,0x3f,sizeof(g));//初始化邻接矩阵 
	for(int i = 0;i < int(edge.size());i ++ )
	{
		int a = edge[i].a;
		int b = edge[i].b;
		int c = edge[i].c;
		g[a][b] = g[b][a] = min(g[a][b],c);//对称存储 
	} 
	
	//邻接矩阵展示
	cout << "———————————————————————————————————————" << endl;
	printf("                          地图信息邻接矩阵如下：                               \n");
	cout << "———————————————————————————————————————"<< endl;
	for(int i = 1;i <= int(cities.size());i ++ )
	{
		for(int j = 1;j <= int(cities.size());j ++ )
		{
			if(g[i][j] != INF)printf("%d ",g[i][j]);
			else cout << "INF ";
		}
		cout << endl;
	} 
	cout << "———————————————————————————————————————"<< endl; 
	cout << endl << endl << endl;
	
	//Prim 
	cout << "选择路径及总cost如下所示：" << endl << endl;
	cout << "———————————————————————————————————————" << endl;
	int ans = 0;//初始化cost 
    memset(dis,0x3f,sizeof(dis));//初始化dist数组 
    memset(st,false,sizeof(st));//初始化st数组 
    memset(pre,-1,sizeof(pre));//初始化pre数组 
    dis[1] = 0;//默认将第一个边加入集合当中 
    for(int i = 0;i < int(cities.size());i ++ )//遍历头结点 
    {
        int t = -1;
        for(int j = 1;j <= int(cities.size());j ++ )//找到与集合相距距离最短的点 
        {
            if((!st[j]) && (t == -1 || dis[t] > dis[j]))t = j;
        }
        if(i > 0)
        {
        	cout << "         第" << i << "次选择路径为："<< Q_to_name[pre[t]] << " -> " << Q_to_name[t] << " 长度为：" << g[pre[t]][t] << endl; 
            ans += g[pre[t]][t];//cost累加 
        }
        st[t] = true;//将结点t加入集合 
        for (int j = 1; j <= int(cities.size());j ++ )//更新 
        {  
            if (!st[j] && g[t][j] != 0 && g[t][j] < dis[j])//更新其他点到集合的最短距离 
            {  
                dis[j] = g[t][j];  
                pre[j] = t; // 更新j的前驱节点为t  
            }  
        }  
    }
    printf("\n         最小生成树代价为：%d\n",ans);
    cout << "———————————————————————————————————————" << endl;
}
void init_Prim2()
{	
	//初始化+数据导入 
	memset(h, -1, sizeof(h));//头结点初始化为-1 
	idx = 0;//节点初始化 
	for(int i = 0;i < int(edge.size());i ++ )
	{
		//读取边内容，构造邻接表 
		int a = edge[i].a;
		int b = edge[i].b;
		int c = edge[i].c;
		//无向图加两次边 
		add(a,b,c);
		add(b,a,c);
	} 
	
	//路径展示 
	cout << "———————————————————————————————————————" << endl;
	printf("                       地图信息路径如下，共%d条路径：                          \n",int(edge.size()));
	cout << "———————————————————————————————————————"<< endl;
	for(int i = 1;i <= int(cities.size());i ++ )//遍历头结点 
	{
		cout << "            " << Q_to_name[i] << " : ";
		for(int j = h[i];j != -1;j = ne[j])//遍历边界点 
		{
			if(j == h[i])cout << Q_to_name[e[j]];
			else cout << " -> " << Q_to_name[e[j]];
		}
		cout << endl;
	}
	cout << "———————————————————————————————————————"<< endl;
	cout << endl << endl << endl;
	
	//Prim
	cout << "选择路径及总cost如下所示：" << endl << endl;
	cout << "———————————————————————————————————————" << endl;
	memset(dist, 0x3f, sizeof(dist));//初始化dist数组 
	dist[1] = 0;//默认首选第一个点，将第一个点加入集合 
	int ans = 0;//初始化总cost 
	for (int i = 0; i < int(edge.size());i ++ )//遍历头结点 
	{
		int t = -1;
		for (int j = 1; j <= int(edge.size());j ++ )//遍历边界点，每次找到距集合最近的点
		{
			if (vis[j])continue;//如果已存在集合，则跳过 
			else if (t < 0 || dist[j] < dist[t])t = j; 
		}
		//输出选择路径 
		for (int k = h[t]; k != -1; k = ne[k])//遍历新加入节点的所有临边 
		{
			int j = e[k];
			if (vis[j] && w[k] == dist[t])//找到与加入边权相同的那条边 
			{
				cout << "         第" << i << "次选择路径为："<< Q_to_name[j] << " -> " << Q_to_name[t] << " 长度为：" << w[k] << endl;//输出路径 
				ans += dist[t];//cost累加 
				break;
			}
		}
		for(int k = h[t]; k != -1; k = ne[k])dist[e[k]] = min(dist[e[k]], w[k]); //更新其他点到集合的最短路径 
		vis[t] = 1;//将该点加入集合 
	}
	cout << endl << "         最小代价为：" << ans << endl;
	cout << "———————————————————————————————————————" << endl;
}
void init_Kruskal1()
{
	//初始化+数据导入 
	memset(g,INF,sizeof(g));//初始化邻接矩阵 
	for(int i = 0;i < int(edge.size());i ++ )
	{
		int a = edge[i].a;
		int b = edge[i].b;
		int c = edge[i].c;
		g[a][b] = g[b][a] = min(g[a][b],c);//对称存储 
	} 
	
	//邻接矩阵展示
	cout << "———————————————————————————————————————" << endl;
	printf("                          地图信息邻接矩阵如下：                               \n");
	cout << "———————————————————————————————————————"<< endl;
	for(int i = 1;i <= int(cities.size());i ++ )
	{
		for(int j = 1;j <= int(cities.size());j ++ )
		{
			if(g[i][j] != INF)//若两点之间存在边 
			{
				printf("%d ",g[i][j]);//输出 
			}
			else cout << "INF ";//否则输出INF，表示无边 
		}
		cout << endl;
	} 
	cout << "———————————————————————————————————————"<< endl; 
	cout << endl << endl << endl;
	
	//读取邻接矩阵获取边信息 
	vector<Edge> o; 
	//无向图边的存储为对称矩阵，对边信息进行提取只需对上三角或下三角矩阵进行遍历即可，在这里遍历下三角矩阵 
	for(int i = 1;i <= int(cities.size());i ++ )
	{
		for(int j = 1;j <= i;j ++ )
		{
			if(g[i][j] != INF)//若两点之间存在边 
			{
				o.push_back({j,i,g[i][j]});//则存入 
			}
		}
	} 
	
	//Kruskal + 并查集 + 排序(小根堆) 
	cout << "选择路径及总cost如下所示：" << endl << endl;
	cout << "———————————————————————————————————————" << endl;
	printf("       共%d个有效地点，故进行%d条边的选择：\n",int(cities.size()),int(cities.size()) - 1);
	sort(o.begin(),o.end(),cmp);//边按权值升序排序，依次取较小边权进行操作 
	for(int i = 1;i <= int(cities.size());i ++ )p[i] = i;//初始化并查集数组 
	int ans = 0,idx = 0;//对应总cost 路径选择次序 
	for(int i = 0;i < int(edge.size());i ++ )//依次遍历边 
	{
		int a = edge[i].a;
        int b = edge[i].b;
        int c = edge[i].c;
        a = find(a);
        b = find(b);
        //若该边所在点未在集合之中 
        if(find(a) != find(b))
        {
            p[find(a)] = find(b);//加入集合 
            ans += c;//cost累加 
            printf("       第%d次选择的路径为：",++ idx);
            cout << Q_to_name[a] << " -> " << Q_to_name[b] << " 路径长度为：" << c << endl;
        }
	}
	cout << endl << "       最小生成树代价为：" << ans << endl; 
	cout << "———————————————————————————————————————" << endl;
}
void init_Kruskal2()
{
	//初始化+数据导入 
	memset(h, -1, sizeof(h));//头结点初始化为-1 
	idx = 0;//节点初始化 
	for(int i = 0;i < int(edge.size());i ++ )
	{
		//读取边内容，构造邻接表 
		int a = edge[i].a;
		int b = edge[i].b;
		int c = edge[i].c;
		//无向图加两次边 
		add(a,b,c);
		add(b,a,c);
	} 
	
	//路径展示 
	cout << "———————————————————————————————————————" << endl;
	printf("                       地图信息路径如下，共%d条路径：                          \n",int(edge.size()));
	cout << "———————————————————————————————————————"<< endl;
	for(int i = 1;i <= int(cities.size());i ++ )//遍历头结点 
	{
		cout << "            " << Q_to_name[i] << " : ";
		for(int j = h[i];j != -1;j = ne[j])//遍历边界点 
		{
			if(j == h[i])cout << Q_to_name[e[j]];
			else cout << " -> " << Q_to_name[e[j]];
		}
		cout << endl;
	}
	cout << "———————————————————————————————————————"<< endl;
	cout << endl << endl << endl;
	
	//读取邻接表获取边信息 
	vector<Edge> o; //定义临时数组o，用于从邻接表中读取信息 
	for(int i = 1;i <= int(cities.size());i ++ )//遍历头结点 
	{
		for(int j = h[i];j != -1;j = ne[j])//遍历边节点 
		{
			o.push_back({i,e[j],w[j]});//i为头结点编号，e[j]为边界点编号，w[j]为 i -> e[j] 边的权值 
		}
	} 
	
	//Kruskal + 并查集 + 排序(小根堆) 
	cout << "选择路径及总cost如下所示：" << endl << endl;
	cout << "———————————————————————————————————————" << endl;
	printf("       共%d个有效地点，故进行%d条边的选择：\n",int(cities.size()),int(cities.size()) - 1);
	sort(o.begin(),o.end(),cmp);//边按权值升序排序，依次取较小边权进行操作 
	for(int i = 1;i <= int(cities.size());i ++ )p[i] = i;//初始化并查集数组 
	int ans = 0,idx = 0;//对应总cost 路径选择次序 
	for(int i = 0;i < int(edge.size());i ++ )//依次遍历边 
	{
		int a = edge[i].a;
        int b = edge[i].b;
        int c = edge[i].c;
        a = find(a);
        b = find(b);
        //若该边所在点未在集合之中 
        if(find(a) != find(b))
        {
            p[find(a)] = find(b);//加入集合 
            ans += c;//cost累加 
            printf("       第%d次选择的路径为：",++ idx);
            cout << Q_to_name[a] << " -> " << Q_to_name[b] << " 路径长度为：" << c << endl;
        }
	}
	cout << endl << "       最小生成树代价为：" << ans << endl; 
	cout << "———————————————————————————————————————" << endl;
}
int main()
{
    int flag = INF;//菜单标识符 
    while(flag != 666)
    {
    	system("cls");//清空程序框内容
		display();//展示菜单 
		printf("请选择您想要实现的功能序号：");
		scanf("%d",&flag);
		switch(flag)//匹配功能 
		{
			case 1:
				system("cls");//清空程序框内容
				read();//读取文件内容及处理 
				cout << "路径读取已完成！！！请输入-1返回：";
				cin >> flag;
				if(flag == -1)continue;
				break;
			case 2:
				system("cls");//清空程序框内容
				init_Prim1();//以邻接矩阵为存储结构 Prim 
				cout << "请输入-1返回："; 
				cin >> flag;
				if(flag == -1)continue;
				break;
			case 3:
				system("cls");//清空程序框内容
				init_Prim2();//以邻接表为存储结构 Prim 
				cout << "请输入-1返回："; 
				cin >> flag;
				if(flag == -1)continue;
				break;
			case 4:
				system("cls");//清空程序框内容
				init_Kruskal1();//以邻接矩阵为存储结构 Kruskal 
				cout << "请输入-1返回："; 
				cin >> flag;
				if(flag == -1)continue;
				break;
			case 5:
				system("cls");//清空程序框内容
				init_Kruskal2();//以邻接表为存储结构 Kruskal
				cout << "请输入-1返回："; 
				cin >> flag;
				if(flag == -1)continue;
				break;
			case 6:
				system("cls");//清空程序框内容
				printf(
				    "                ********\n"
				    "               ************\n"
				    "               ####....#.\n"
				    "             #..###.....##....\n"
				    "             ###.......######              ###            ###\n"
				    "                ...........               #...#          #...#\n"
				    "               ##*#######                 #.#.#          #.#.#\n"
				    "            ####*******######             #.#.#          #.#.#\n"
				    "           ...#***.****.*###....          #...#          #...#\n"
				    "           ....**********##.....           ###            ###\n"
				    "           ....****    *****....\n"
				    "             ####        ####\n"
				    "           ######        ######\n"
				    "##############################################################\n"
				    "#...#......#.##...#......#.##...#......#.##------------------#\n"
				    "###########################################------------------#\n"
				    "#..#....#....##..#....#....##..#....#....#####################\n"
				    "##########################################    #----------#\n"
				    "#.....#......##.....#......##.....#......#    #----------#\n"
				    "##########################################    #----------#\n"
				    "#.#..#....#..##.#..#....#..##.#..#....#..#    #----------#\n"
				    "##########################################    ############\n"
				    );
				cout << "谢谢您的使用！再见！！！" << endl; 
				flag = 666;
				break;
		} 
	}

}