B.Contiguous Repainting
不管怎么操作,最后一定有连续的KKK个颜色相同,其它的格子可以随便染。
枚举这KKK个颜色相同的区间即可。
C.Tetromino Tiling
研究一下四米诺的组合:
- T,S,Z根本放不上去
- O可以全部直接放上去
- 剩下的组合只有: 2L,2J,2*I,L+J+I
分类讨论即可。
D.K-th K
贪心往前放就是了
E.Next or Nextnext
再次读错题浪费时间:
For each 1≤i≤N1\leq i\leq N1≤i≤N,at least one of the following holds:pi=aip_i=a_ipi=aiandppi=aip_{p_i}=a_ippi=ai
读成了至少有两个iii分别满足pi=aip_i=a_ipi=ai,ppi=aip_{p_i}=a_ippi=ai…
我服我自己。。。
emmm,一道神奇的基环树森林结论题:
p→ap\to ap→a
ppp是一个1−N1-N1−N的排列,所以构图i→pii\to p_ii→pi,得到若干个环。
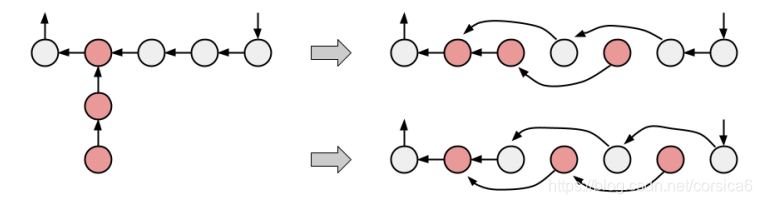
在ppp变化成aaa的过程中,每个点要么保持i→pii\to p_ii→pi,要么转化成i→ppii\to p_{p_i}i→ppi,分类讨论:
- 保持原状,即pi=ai(1≤i≤N)p_i=a_i(1\leq i\leq N)pi=ai(1≤i≤N),图的形态不变
- 所有iii指向ppip_{p_i}ppi,即ppi=aI(1≤i≤N)p_{p_i}=a_I(1\leq i\leq N)ppi=aI(1≤i≤N)
对于奇环,变成同构的另一个环。
对于偶环,拆分成偶数点和奇数点分别构成的两个大小相同的环。 - 若环中部分点指向pip_ipi,部分点指向ppip_{p_i}ppi,则变成了一棵由一个环和若干指向环的链构成的基环内向树。
a→pa\to pa→p
考虑由aaa反推ppp:
- 单独考虑每个大小的环,组合一下
- 对于一颗基环内向树,找到所有相邻的指向环的链,假设当前链边数为aaa,链顶与上一个链顶在环上的距离边数为bbb:
若b<ab<ab<a,有0种方案;若a=ba=ba=b有1种方案;若a<ba<ba<b,有2种方案。
乘法原理合并即可。
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=1e5+10,mod=1e9+7;
int n,ans=1;
int t[N],a[N],vs[N],d[N],dr[N],f[N];
bool cir[N];
inline int ad(int x,int y){x+=y;return x>=mod?x-mod:x;}
void sol(int x)
{
int nw=0,fi=0,sc,pre;
for(;cir[x];x=a[x]){
++nw;cir[x]=false;
if(!dr[x]) continue;
if(!fi) {fi=sc=nw;pre=dr[x];}
else{
if(nw-sc<dr[x]) ans=0;
else if(nw-sc>dr[x]) ans=ad(ans,ans);
sc=nw;
}
}
if(!fi) t[nw]++;
else{
nw=fi-sc+nw;
if(nw<pre) ans=0;
else if(nw>pre) ans=ad(ans,ans);
}
}
int main(){
int i,j,k;
scanf("%d",&n);
for(i=1;i<=n;++i) {scanf("%d",&a[i]);d[a[i]]++;}
for(i=1;i<=n;++i) if(!vs[i]){
vs[i]=i;
for(j=a[i];!vs[j];j=a[j]) vs[j]=i;
if(vs[j]^i) continue;
for(;!cir[j];j=a[j]) cir[j]=true;
}
for(i=1;i<=n;++i)
if((cir[i] && d[i]>2)||((!cir[i])&& d[i]>1))
{puts("0");return 0;}
for(i=1;i<=n;++i) if(!d[i]){
for(k=0,j=i;(!cir[j]);j=a[j]) k++;
dr[j]=k;
}
for(i=1;i<=n;++i) if(cir[i]) sol(i);
if(!ans) {puts("0");return 0;}
f[0]=1;
for(i=1;i<=n;++i) if(t[i]){
for(j=1;j<=t[i];++j){
if(i>1 && (i&1)) f[j]=ad(f[j-1],f[j-1]);
else f[j]=f[j-1];
if(j>1) f[j]=ad(f[j],(ll)f[j-2]*(j-1)*i%mod);
}
ans=(ll)ans*f[t[i]]%mod;
}
printf("%d",ans);
return 0;
}
F.Black Radius
先假设树上所有点都是关键点:
设f(x,d)f(x,d)f(x,d)表示距离xxx小于等于ddd的点集合。
为避免算重,对于所有集合相同的f(x,d)f(x,d)f(x,d)只取ddd最小的一个计入答案。
不考虑f(x,d)f(x,d)f(x,d)为全集的情况(最后再ans+1ans+1ans+1),所需要求出的就是:
did_idi:最大的ddd满足f(i,0−d)f(i,0-d)f(i,0−d)均可取且f(x,di)f(x,d_i)f(x,di)不为全集。
上界did_idi的具体求法:
将点iii作为根,设离iii最远的点的距离为mximx_imxi,显然di<mxid_i<mx_idi<mxi,且∀j∈soni\forall j\in son_i∀j∈soni,∃f(i,d)≠f(j,d−1)\exists f(i,d)\neq f(j,d-1)∃f(i,d)̸=f(j,d−1)。
设删掉jjj子树后离iii最远的点的距离为pmxipmx_ipmxi,则di−2<pmxid_i-2<pmx_idi−2<pmxi。
故di=min(max(pmxi)+1,mxi−1)d_i=\min(\max(pmx_i)+1,mx_i-1)di=min(max(pmxi)+1,mxi−1)。
考虑有些点不是关键点的情况:
那么对于每个非关键点存在一个下界qiq_iqi:最小的qqq满足f(q,di)f(q,d_i)f(q,di)均可取且为某个关键点f(j,d)f(j,d)f(j,d)的点集。
下界qiq_iqi的具体求法:
将点iii看做根,考虑j∈sonij\in son_ij∈soni的所有的内部有关键点的子树j′j'j′,qi=max(maxdepj′)q_i=\max(maxdep_{j'})qi=max(maxdepj′),即f(i,qi)f(i,q_i)f(i,qi)必须要把这些子树全部覆盖。
2遍dfsdfsdfs求得di,qid_i,q_idi,qi。








 本文详细解析了Atcoder AGC008比赛中的B到F五道题目,涉及颜色区间枚举、四米诺组合讨论、贪心策略、基环树森林结论以及黑点半径问题。对于每道题目,作者给出了思路和解题方法,包括连续染色、四米诺拼图、寻找第K个K、判断路径条件和计算黑点半径等。
本文详细解析了Atcoder AGC008比赛中的B到F五道题目,涉及颜色区间枚举、四米诺组合讨论、贪心策略、基环树森林结论以及黑点半径问题。对于每道题目,作者给出了思路和解题方法,包括连续染色、四米诺拼图、寻找第K个K、判断路径条件和计算黑点半径等。
















 723
723

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








