【模板】带花树-bzoj4405: [wc2016]挑战NPC

---

带花树

带花树是一种求解一般图最大匹配的算法。时间复杂度上限$O(n^3)$。

首先推荐一篇很好理解的博客。

一般图相较于二分图就是图上多了奇环，而“花”指的就是图中的奇环。对于奇环的匹配：首先在环内尽可能地匹配显然是最优的，若环上有$2k+1$个点，则环内可以用$k$条边匹配任意$2k$个点，剩下一个未匹配的点可以向外匹配，这个未匹配点是根据需要回溯时才确定的，所以将奇环缩点，用并查集维护是否在同一个“花”内。

具体来说，我们每次选择一个未匹配点$bfs$进行增广(将该点标记为$S$)，并将所有访问到的点标记为$S$或$T$(出发点标记为$S$)。为了回溯连边还需要用到$pre$数组，对于每个标记为$T$的点$i$，$pr{e}_i$表示当前$bfs$中$i$点第一次是被哪个结点访问到的。

一颗$bfs$树形如：

其中起点为$s$，黑点标记为$S$，红点标记为$T$。$S,T$标记则相当于二分图匹配中的出度和入度一样。

如同二分图匹配，每次只增广$S$标记点，将需要增广的点逐个压入队列(一开始队列中只有起点$S$)依次处理。

如果$dfs$的话不能之间判断增广点的类型，甚至可能增广到一个首尾都是自己的奇环，所以$bfs$做的实际上是一个给点定型的操作，缩点后转成二分图。

模拟一下从当前点$x$向外扩展到$v$的情况：

1. $x$和$v$在同一个“花”内，或者$v$有标记$T$(偶环)，跳过
   偶环情况如图：
   
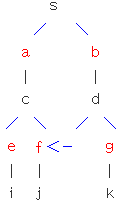
2. $v$没有标记，将$v$标记为$T$
   2.1. $v$已匹配，则将它的匹配点$matc{h}_v$标记为$S$，加入$bfs$队列进行增广
   所以实际上$bfs$树中除根结点外的$S$标记点都是已匹配点且它的匹配点为它的父亲结点(标记为$T$)。
   2.2. $v$为未匹配点，则找到了一条起点终点都为未匹配点的增广路。
   从这个$T$开始，将$v$点的匹配设为$pr{e}_v$，$pr{e}_v$的匹配也改成$v$，再向上跳到原本$matc{h}_{pr{e}_v}$的位置($pr{e}_v$的父亲结点)，不断如此操作直到根。
3. $v$有标记$S$，则找到了一个奇环，需要进行缩点。如将下图中的奇环缩成一个点，且点标记为$S$。从这个大点中的任意一个向外增广都是合法的。所以找到$lca(x,v)$后遍历这个环，将环中标记为$T$的点改成标记为$S$并压入队列进行增广。
   
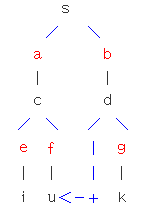
   那么此时若增广路通过回溯到某个在奇环上的点$i$，则表示$i$在环上的两条邻边不能选，而将其它不相交边依次选中。
   注意到如果$i$点原本就标记为$S$(它的邻边原本就都不选)，则不需要改变。
   但是如果$i$点原本标记为$T$，回溯时跳原本的$matc{h}_i$会向下跳到一个原本就标记为$S$的点，那么就需要将环上所有原本就标记为$S$的点的$pre$设成其儿子结点(具体来说就是在跳$lca$时记录每个标记为$T$的点$u$，将$pr{e}_{pr{e}_u}$赋值为$u$)。而对于最底层的标记为$S$点(如图中的$u$)，将其$pre$设成这条非树边的另一端即可。

p.s.每次增广成功就直接返回了，所以下一次增广前记得清空$queue$。

---

bzoj4405

将每个筐子拆成三个点。三个点互相连边(均为无向边)。

球可以放进某个箱子就是将球对应的点向对应的筐的三个连边。

答案即为最大匹配数-n。

---

代码

#include<bits/stdc++.h>
using namespace std;
const int N=605,M=1e6+10;

int tk,n,m,e,lim,bs1,bs2,bs3,ans;
int head[N],to[M],nxt[M],tot;
int pre[N],bel[N],f[N],typ[N],vs[N],tim;

inline void lk(int u,int v)
{
	to[++tot]=v;nxt[tot]=head[u];head[u]=tot;
    to[++tot]=u;nxt[tot]=head[v];head[v]=tot;
}

int getfa(int x){return x==f[x]?x:(f[x]=getfa(f[x]));}

inline int lca(int x,int y)
{
	for(tim++;;swap(x,y)) if(x){
		x=getfa(x);
		if(vs[x]==tim) return x;
		vs[x]=tim;x=pre[bel[x]];
	}
}

queue<int>que;

inline void trs(int x,int y,int z)
{
	for(;getfa(x)!=z;x=pre[y]){
		pre[x]=y;y=bel[x];
		if(typ[y]==2) typ[y]=1,que.push(y);
		if(getfa(x)==x) f[x]=z;if(getfa(y)==y) f[y]=z;
	}
}

inline int ext(int s)
{
	int i,j,x,y,lst,z;
	for(i=1;i<=lim;++i) f[i]=i;for(;que.size();que.pop());
	memset(typ,0,sizeof(typ));memset(pre,0,sizeof(pre));
	for(typ[s]=1,que.push(s);que.size();){
		x=que.front();que.pop();
		for(i=head[x];i;i=nxt[i]){
			j=to[i];if(getfa(j)==getfa(x) || typ[j]==2) continue;
			if(!typ[j]){
				typ[j]=2;pre[j]=x;
				if(!bel[j]){
					for(x=j;x;x=lst){
						y=pre[x];lst=bel[y];bel[y]=x;bel[x]=y;
					}
					return 1;
				}
				typ[bel[j]]=1;que.push(bel[j]);
			}else{z=lca(x,j);trs(x,j,z);trs(j,x,z);}
		}
	}
	return 0;
}

inline void sol()
{
	int i,j,x,y;
	memset(head,0,sizeof(head));tot=0;
	memset(bel,0,sizeof(bel));
	scanf("%d%d%d",&n,&m,&e);
	bs1=n;bs2=n+m;bs3=n+m+m;lim=n+m+m+m;
	for(i=1;i<=m;++i){lk(bs1+i,bs2+i);lk(bs2+i,bs3+i);lk(bs1+i,bs3+i);}
	for(i=1;i<=e;++i){
		scanf("%d%d",&x,&y);
		lk(x,bs1+y);lk(x,bs2+y);lk(x,bs3+y);
	}
	ans=0;
	for(i=1;i<=lim;++i) ans+=((!bel[i])&&(ext(i)));
	printf("%d\n",ans-n);
}

int main(){
	for(scanf("%d",&tk);tk;--tk) sol();
    return 0;
}