关于n个tromino覆盖3*n矩形方案数递推式的推导

Tromino

多米诺是$1\times 2$的骨牌。tromino就是$1\times 3$的骨牌(可以弯折)，有两种基本形态(可以旋转)：

---

公式

设$n$个tromino完全覆盖$3\times n$矩形的方案数为$f_n$，则对于$n\ge 6$存在递推式：
$$f_n=f_{n-1}+2f_{n-2}+6f_{n-3}+f_{n-4}-f_{n-6}$$
$f_0=1,f_1=1,f_2=3,f_3=10,f_4=23,f_5=62$。

---

推导

首先从$1\times 2$的多米诺的递推公式说起：

设完全覆盖$2\times n$矩形的方案数为$g_n$，则对$n\ge 2$存在递推式：
$$g_n=g_{n-1}+g_{n-2}$$
$g_0=0,g_1=1$

简单推导如下：
假设当前已填满前$2\times i$块，考虑怎样填可以使得其增加任意$2\times j$块($j\le n-i$)。有两种最基本的覆盖方式：

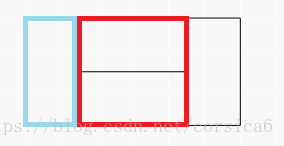
之所以称为最基本的覆盖方式，是因为这两种结构是无法再进一步拆分的，而对于其他方式(如下图)，都可以拆分成这二者。
所以求$g_n$时，它的最后一组基本排列方式只能二选一，所以$g_n=g_{n-1}+g_{n-2}$。

这样看来，对于tromino来说，只需要找出其所有的基本覆盖方式。

首先可以得到以下1+2+5=8种：

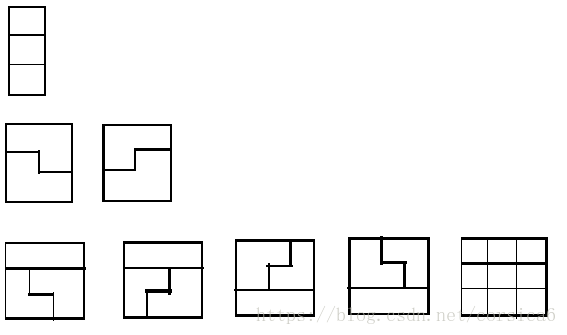
但是还有另外8种较难考虑到的情况：

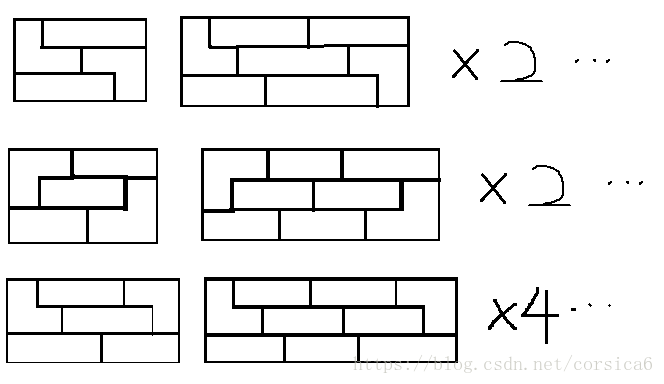
所以可以得到：$$f_n=f_{n-1}+2f_{n-2}+5f_{n-3}+(f_{n-4}+f_{n-7}+...)\times 2+(f_{n-5}+f_{i-8}+...)\times 2+(f_{n-6}+f_{n-9}+...)\times 4$$
而其中
$$(f_{n-4}+f_{n-7}+...)\times 2+(f_{n-5}+f_{n-8}+...)\times 2+(f_{n-6}+f_{n-9}+...)\times 4$$显然是一个分类前缀和的统计，可以由：
$$f_{n-3}=f_{n-4}+2f_{n-5}+5f_{n-6}+(f_{n-7}+f_{n-10}+...)\times 2+(f_{n-8}+f_{n-11}+...)\times 2+(f_{n-9}+f_{n-12}+...)\times 4$$
换元得到：
$$\begin{gathered} (f_{n-4}+f_{n-7}+...)\times 2+(f_{n-5}+f_{n-8}+...)\times 2+(f_{n-6}+f_{n-9}+...)\times 4 \\ =f_{n-3}-f_{n-4}-2f_{n-5}-5f_{n-6}+2f_{n-4}+2f_{n-5}+4f_{n-6} \end{gathered}$$

代回原式得到：
$$f_n=f_{n-1}+2f_{n-2}+6f_{n-3}+f_{n-4}-f_{n-6}$$

那么推导就结束了。

下面是求解n个tromino覆盖3*n矩形方案数的代码(矩阵+特征多项式优化)：

#include<bits/stdc++.h>
#define RI register
using namespace std;
const int N=4e4+100,M=6,mod=998244353;


char s[N];
int n,a[14],re[14],ans;

struct P{int t[14];}nw,b;

int c[10]={0,1,2,6,1,0,998244352};
int as[13]={1,1,3,10,23,62,170,441,1173,3127};

inline int ad(int x,int y){x+=y;return x>=mod?x-mod:x;}
inline int dc(int x,int y){x-=y;return x<0?x+mod:x;}
inline int mul(int x,int y){return 1ll*x*y%mod;}

inline void Ml(int *a,int *b)
{
	RI int i,j,val;
	memset(re,0,sizeof(re));
	for(i=0;i<7;++i)
	 for(j=0;j<7;++j)
	  re[i+j]=ad(re[i+j],mul(a[i],b[j]));
	for(i=12;i>5;--i) if(re[i]){
		val=re[i];
		for(j=0;j<6;++j)
		 re[i-6+j]=ad(re[i-6+j],mul(val,c[6-j]));
		re[i]=0;
	}
	for(i=0;i<=6;++i) a[i]=(re[i]+mod)%mod;
}

inline P fp(P a,int y)
{
	memset(nw.t,0,sizeof(nw.t));
	nw.t[0]=1;
	for(;y;y>>=1,Ml(a.t,a.t))
	 if(y&1) Ml(nw.t,a.t);
	return nw;
}

int main(){
	RI int i,j;P res;
	scanf("%s",s);
	n=strlen(s);
	reverse(s,s+n);
	if(n==1) {printf("%d\n",as[s[0]-'0']);return 0;}
	a[0]=b.t[1]=1;
	for(i=0;i<n;++i){
		if(s[i]!='0') {
			res=fp(b,s[i]-'0');
			Ml(a,res.t);
	    }
		res=fp(b,10);
		memcpy(b.t,res.t,sizeof(b.t));
	}
    for(i=0;i<6;++i) ans=ad(ans,mul(a[i],as[i]));
	printf("%d\n",ans); 
	return 0;
}