-
查找数据元素。
Search(bt, x):在以bt为二叉树的根结点指针的二叉树中查找数据元素x。查找成功时返回该结点的指针;查找失败时返回空指针。
算法实现如下,注意遍历算法中的Visit (bt->data) 等同于其中的一组操作步骤。
二叉树的元素查找算法

BiTree Search(BiTree *bt,elemtype x)
{ / * 在bt为根结点指针的二叉树中查找数据元素x */
BiTree p;
p=bt;
if (p->data= =x) return p; / * 查找成功返回 */
if ( p->lchild!=NULL) / * 在p->lchild为根结点指针的二叉树中查找数据元素x */
return (Search (p->lchild, x) );
if ( p->rchild!=NULL) / * 在p->rchild为根结点指针的二叉树中查找数据元素x */
return (Search (p->rchild, x));
return NULL; / * 查找失败返回 */
} -
求二叉树叶子结点个数
算法:
int CountLeaf2 (BiTree *bt)
{ / * 开始时,bt为根结点所在链结点的指针,返回值为bt的叶子数 */
if (btNULL) return(0);
else if (bt->lchildNULL && bt->rchild==NULL)
return (1);
else
return (CountLeaf2 (bt->lchild)+CountLeaf2 (bt->rchild));
} -
求二叉树的深度运算。
求深度算法同样可以通过遍历操作来实现,算法如下int treehigh (BiTree *bt)
{ int lh,rh,h;
if (bt==NULL) h=0;
else
{ lh=treehigh(bt->lchild);
rh=treehigh (bt->rchild);
h=(1h>rh-1h:rh)+1;
}
return h;
} -
已知结点的前序序列和中序序列分别如下。
前序序列:A B C D E F G
中序序列:C B E D A F G
则可按上述分解求得整棵二叉树。其构造过程如图所示。首先由前序序列得知二叉树的根为A,则其左子树的中序序列为(C B E D),右子树的中序序列为(F G)。反过来得知其左子树的前序序列必为(B C D E),右子树的前序序列为(F G)。类似地,可由左子树的前序序列和中序序列构造得A的左子树,由右子树的前序序列和中序序列构造得A的右子树。

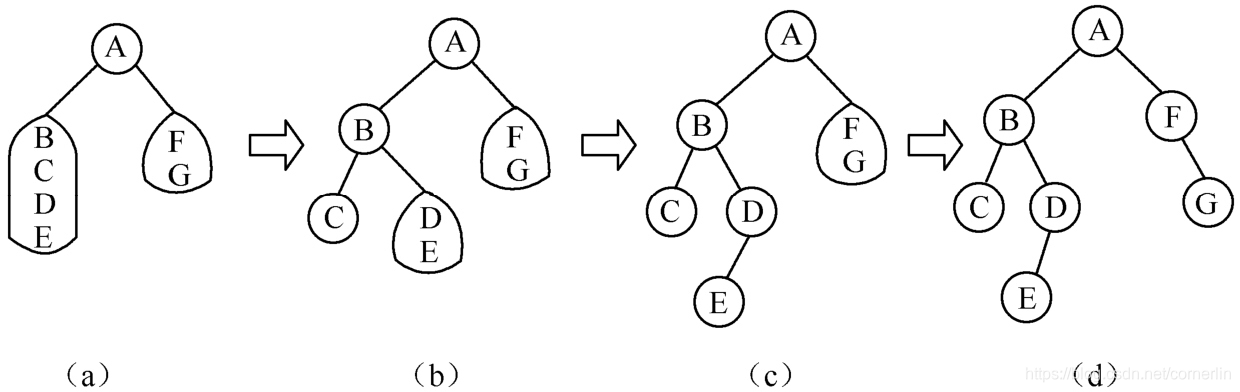
数据结构(c语言版 5.2.2 二叉树的其他操作举例)
最新推荐文章于 2022-01-13 16:51:56 发布
 本文深入探讨了二叉树的查找、叶子节点计数及深度求解算法,通过具体实例展示了算法的实现过程,包括递归查找数据元素、计算叶子节点数量及确定二叉树深度。同时,还介绍了如何根据前序和中序序列构建二叉树。
本文深入探讨了二叉树的查找、叶子节点计数及深度求解算法,通过具体实例展示了算法的实现过程,包括递归查找数据元素、计算叶子节点数量及确定二叉树深度。同时,还介绍了如何根据前序和中序序列构建二叉树。





















 864
864

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








