5.23 Matplotlib

最新推荐文章于 2025-03-02 10:37:28 发布

alt_ctrl

最新推荐文章于 2025-03-02 10:37:28 发布

阅读量297

点赞数

CC 4.0 BY-SA版权

分类专栏：作业

本文链接：https://blog.youkuaiyun.com/control_xu/article/details/80495148

作业专栏收录该内容

20 篇文章

订阅专栏

本文通过几个Python代码示例展示了如何使用matplotlib进行图表绘制，包括曲线图、参数比较图及核密度估计图，并利用numpy和scipy库进行数据生成与分析。

import matplotlib.pyplot as plt
import numpy as np
import math

x = np.linspace(0,2,1000)
y = np.power(np.sin(x-2),2) * np.power(math.exp(1),-np.power(x,2))

plt.plot(x,y)
plt.xlabel("x-axis")
plt.ylabel("y-axis")
plt.title("11.1 figure")
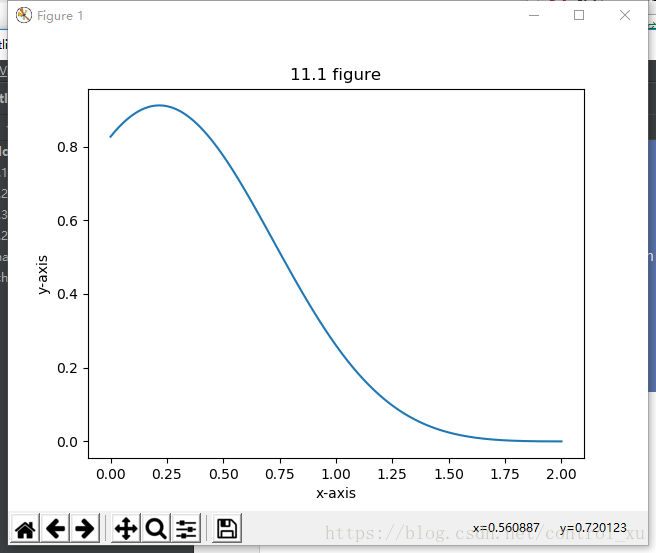
plt.show()

没什么好说的，用内置的指数函数，三角函数，然后生成一个x的序列再对应生成f（x），再plot和show出来就好了。

结果如下

import matplotlib.pyplot as plt
import numpy as np

X = np.random.normal(size= (20,10))
z = np.random.normal(size = (20,1))
b = np.random.normal(size = (10,1))
y = np.dot(X,b) + z

b1, _,__, ___ = np.linalg.lstsq(X, y)

plt.plot(np.array([i for i in range(10)]), b, 'xr' ,label='true parameters')
plt.plot(b1,'.b' ,label='estimated parameters')
plt.xlim((-1,10))
plt.ylim((-2,2))
plt.xlabel('index')
plt.ylabel('value')
plt.title('Parameter plot')
plt.legend()
plt.show()

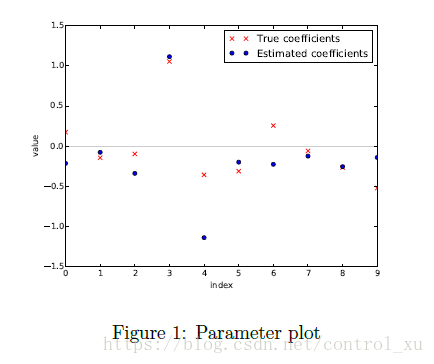
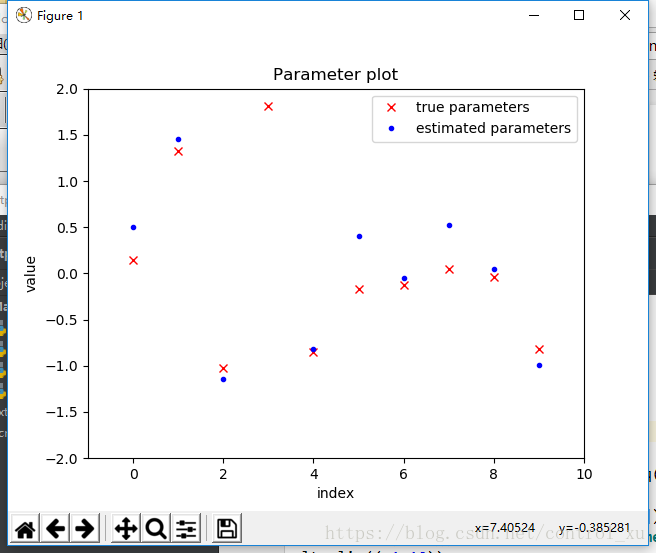
题目的意思是自己给出一个X，b和z，然后y=Xb+z。

之后用y和X反过来估计b（和z）的值

这里我用了numpy.linalg中内置的lstsq函数，即最小二乘法，返回的第一个参数就是b。

之后在同一个图中画出各个点进行比较。

输出效果如图

import matplotlib.pyplot as plt
import numpy as np
import scipy.stats


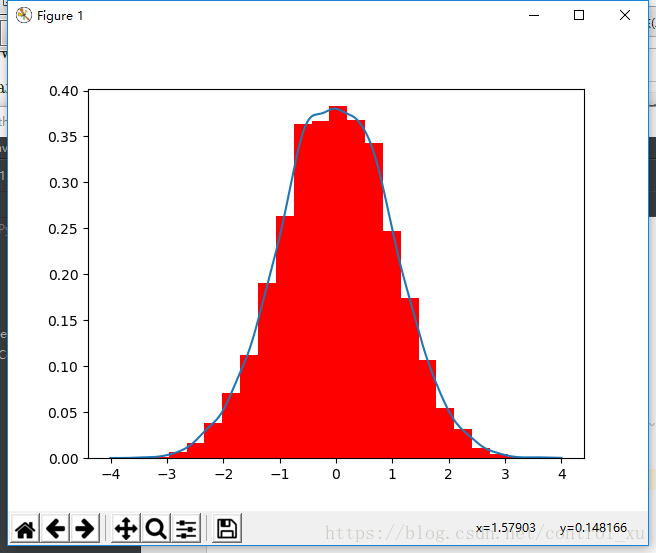
z = np.random.normal(size = 10000)
kernel = scipy.stats.gaussian_kde(z)
data = np.linspace(-4,4,10000)

n, bins, patches = plt.hist(z, bins = 25, color= 'r', normed = True)
plt.plot(data, kernel.evaluate(data))
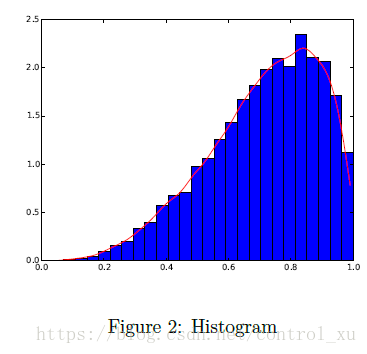
plt.show()

题目的意思是z是满足一个满足同一分布的10000个样本的向量，这个分布自选。然后生成一个这样的有25个柱子的柱形图，同时有一个使用高斯核密度估计法生成的密度估计。scipy.stats有内置的gaussian_kde函数，但是不知道怎么用。

最后试来试去，就生成了一个均匀分布的数据data，然后让这个核作用于data。然后画出来。跟要求的差不多，不过纵坐标有点看不懂。

效果图如图