二分查找-面试题之二

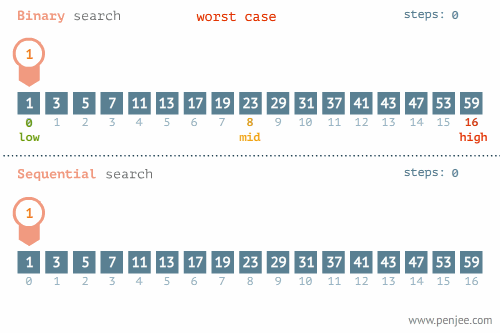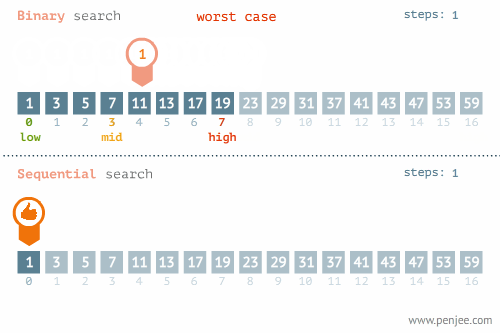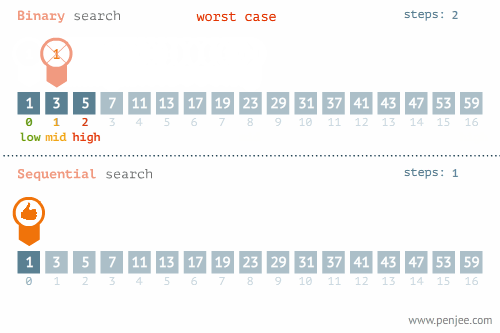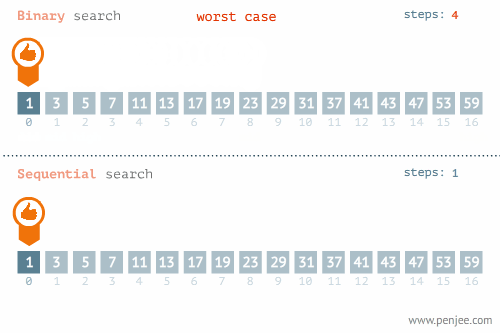
二分查找过程：通过将有序的数组(注意是有序)折半，首先将目标元素与数组中间的数字做比较，如果目标元素值小于中间元素,则将数组前半部分进行折半查找，将前半部分的mid元素与目标元素做比较，如果目标元素小于mid元素，同理将数组再折半在前半部分(此时是数组的1/4部分)二分查找，以此类推；反之，若目标元素值大于数组中间元素，则向后半部分查找。（见下面动图1）

线性查找（见动图2）

二分查找(折半搜索)目的：查找有序结构中某一特定元素

（图转载自：https://www.cnblogs.com/tflsnoi/p/8071970.html）

时间复杂度：log(n),n是元素的个数

空间复杂度：o(1)

缺点：

前提条件必须是有序结构。

优点：

每次都是折半查询，查询次数少，效率高，性能较好

适用场景：不经常变动，查询频繁且有序的结构。

迭代实现：

public  static  int binarySearch(int arr[] ,int target){
    int mid ;
    int start = 0;
    int end =arr.length-1;
    while (start <= end){
        mid = (end -start)/2+start;
        if (target<arr[mid]){
            end = mid - 1;
        }
        else if (target>arr[mid]){
            start = mid + 1;
        }
        else {
            return mid;
        }
    }
    return  -1;

}

/*
 * 非递归方式二分查找法 ，返回目标元素的下标
 * target 要查找的目标元素
 * mid 中间元素下标
 * start 数组开始元素下标
 * end 数组末尾元素下标
 * 运行下来大概需要3000ns左右 慢的时候达到4000ns  没有递归方式快，递归需要1000ns左右
 * */

递归实现：

public  static  int binarySearch2(int []arr,int start ,int end ,int target){
    int mid =  start+ (end - start)/2;
    if (start>end){
        return  -1;
    }
    if (arr[mid] < target){
       return  binarySearch2(arr,mid+1,end,target);

    }
    else if (arr[mid] > target){
       return binarySearch2(arr,start,mid-1,target);
    }
    else if (arr[mid] == target){
        return  mid;
    }
        return -1;

}