优先队列实现哈夫曼树——中堂系的困难任务

 

题目链接CDOJ中堂系的困难任务

 

 

 

 

 

 

 

 

 

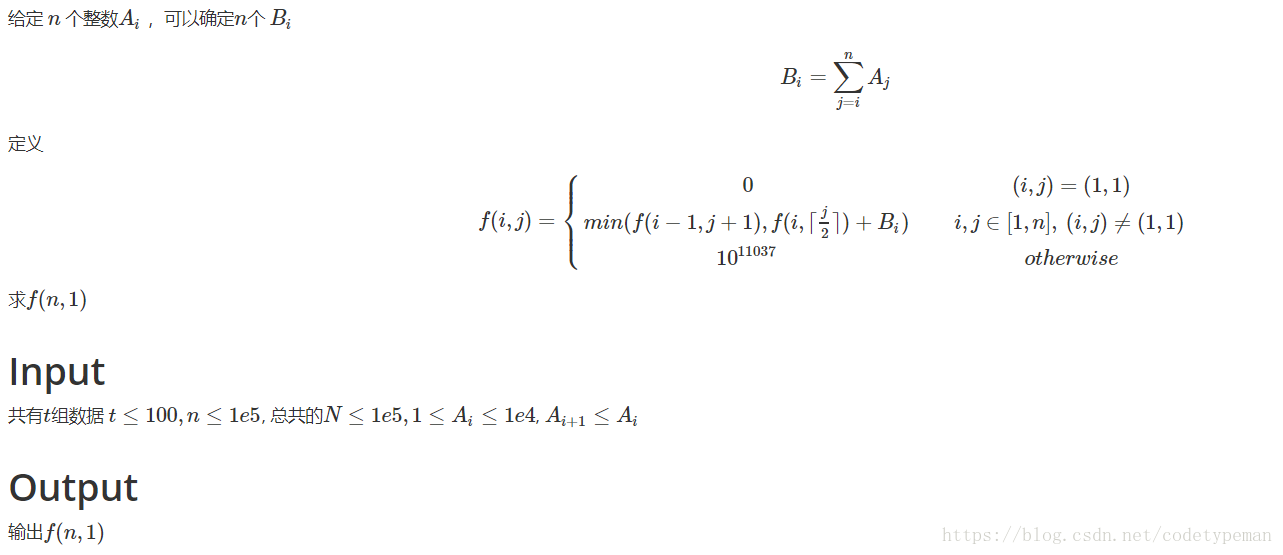
Sample input and output

Sample Input	Sample Output
3 3 1 1 1 5 28 26 25 24 1 10 996 901 413 331 259 241 226 209 139 49	5 233 11037

 

按照题目给的公式稍微推一下发现f ( i,  j) = min(f (i -1 ,j+1 ) , f ( i, j/2 ) +b[ i ] ) 这个公式与哈夫曼树的dp式有些相似，

哈夫曼树的dp推导

先对元素从大到小排序。 
设f（ i , j ）表示现在已经做了前i个元素，还空出来j个叶子节点的最小代价。 
第一种转移显然，就是把第i+1个元素放到一个叶子节点上，f ( i+1,j−1 )=f (i , j )。 
第二种转移就是把当前剩下的叶子节点都再生成出两个节点来,代价是把当前的剩下元素全部加深了一层，所以

f( i,2∗j )=f( i,j )+b[ i+1 ]。    Ans=min(fn,k)

所以题目的公式就是哈夫曼树的推导式；f （n，1） 就是最小带权路径和；

然后看样例发现恰好是这样,逃....ε=ε=ε=┏(゜ロ゜;)┛

所以直接用优先队列模拟堆实现，类比合并果子那个题

#include<iostream>
#include<iomanip>
#include<cstdio>
#include<algorithm>
#include<cmath>
#include<queue>
using namespace std;
const int maxn=1e5+7;
int t;
int a[maxn];
int b[maxn];
int n;
int main()
{
    cin>>t;
    while(t--)
    {
        cin>>n;
        priority_queue<long long,vector<long long > ,greater<long long > > q;
        long long cnt=0;
        for(int i=1;i<=n;i++)
            {
                cin>>a[i];
                q.push(a[i]);
                cnt+=a[i];
            }

        long long ans=0;
        while(q.size()>1)
        {
            long long f1=q.top();
            q.pop();
            long long f2=q.top();
            q.pop();
            ans+=f1+f2;
            q.push(f1+f2);
        }
        cout<<ans<<endl;

        //    cout<<ans-cnt<<endl;



    }
    return 0;
}

 

 

哈夫曼树知识补充：

哈夫曼树

给定n个权值作为n个叶子结点，构造一棵二叉树，若带权路径长度达到最小，称这样的二叉树为最优二叉树，也称为哈夫曼树(Huffman Tree)。哈夫曼树是带权路径长度最短的树，权值较大的结点离根较近。

对于一颗哈夫曼树，我们把所有节点排序，权值大的必定层数较低，f[i][j]代表已经放了i-1个叶子节点，正准备放置Ai，该层还有j个空节点，我们可以选择在空节点上放一个叶子节点，从而转移到状态f[i+1][j-1]，或者选择移动到下一层，即转移到f[i][j*2]，该树权值增大量剩下节点的总权值。