牛客寒假算法集训营3VP

最新推荐文章于 2025-12-01 17:13:03 发布

原创最新推荐文章于 2025-12-01 17:13:03 发布 · 748 阅读

11 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #c++ #数据结构 #动态规划

本文讨论了几种编程竞赛中常见的数学问题，包括基于奇偶性分析的博弈、利用数的性质和模运算、枚举法、概率计算以及动态规划求解最优化问题。展示了如何通过编写AC代码解决这些数学和逻辑挑战。

1.简单的博弈

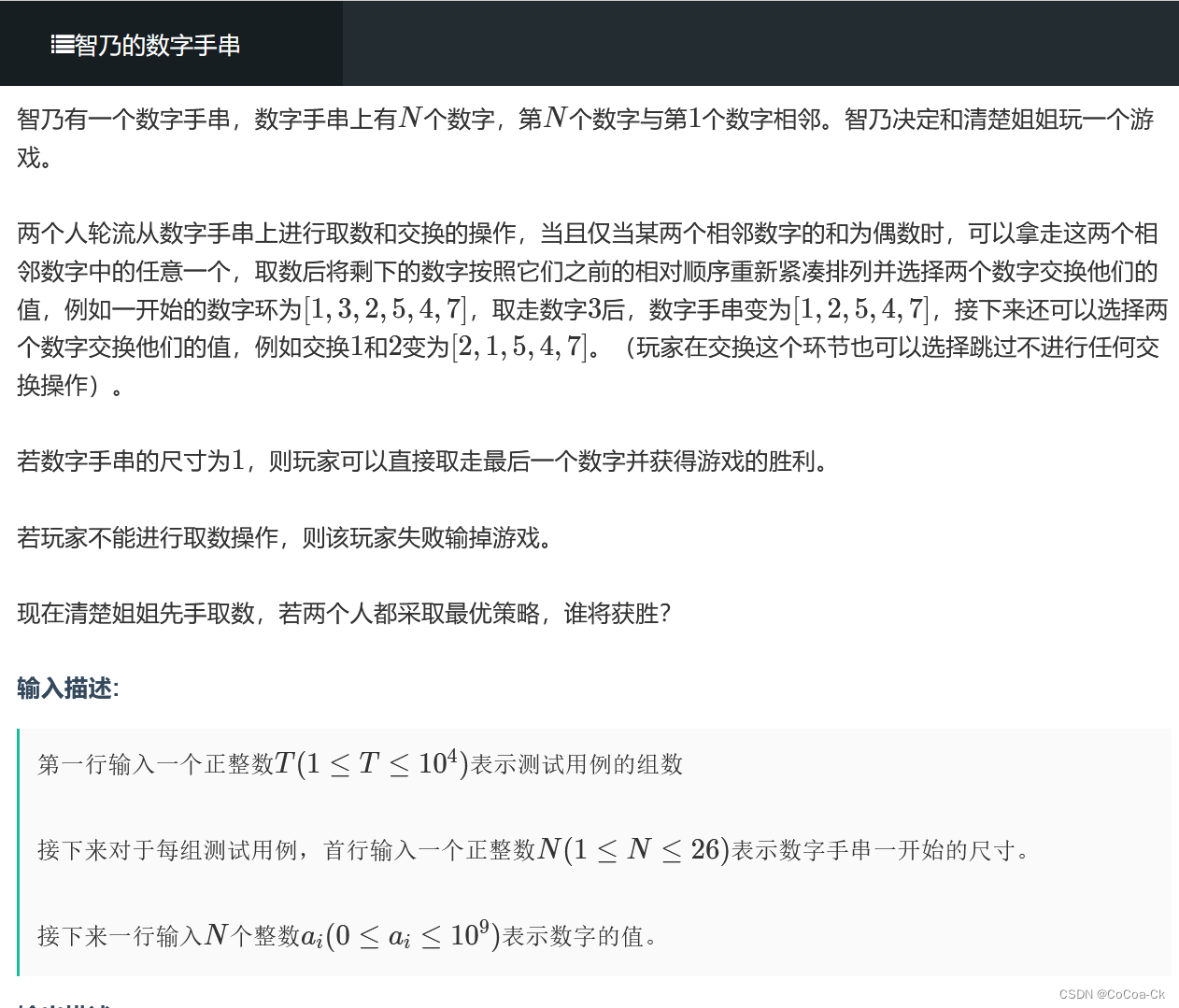
何时可以交换？即相邻的数为奇数与奇数或者偶数和偶数，不可以的一定是121212.。。。

即最终不能拿的一定是偶数个，假如qcjj要赢那么必须有奇数个，即一开始若有偶数个，那么她一定输，若是奇数个，则胜。

下面是AC代码：

#include<bits/stdc++.h>
using namespace std;
int t,n,cnt,w;
int main(){
    cin>>t;
    while(t--){
        cin>>n;
        for(int i=1;i<=n;i++) cin>>w;
        if(n%2==0){
            cout<<"zn"<<endl;
        }
        else cout<<"qcjj"<<endl;
    }
}

2.数学

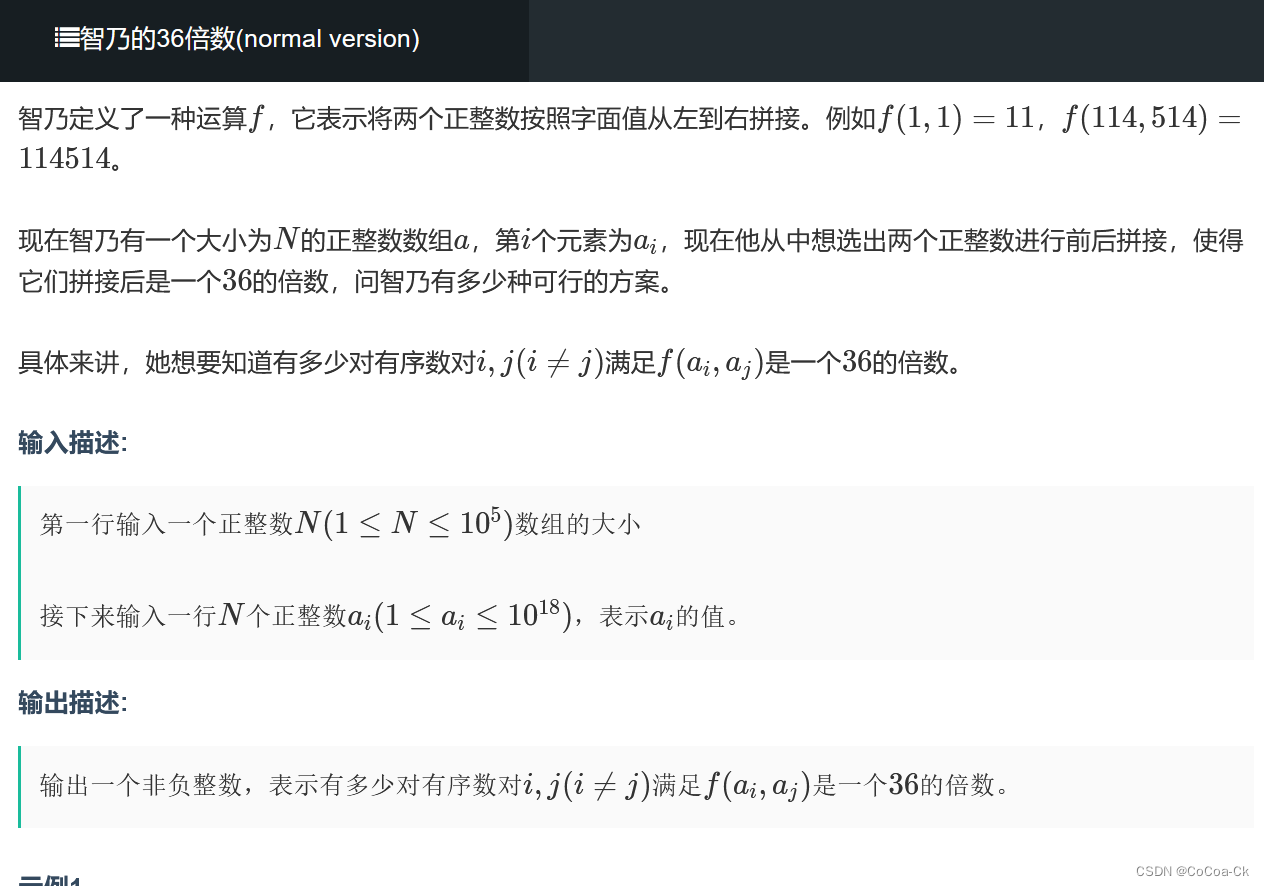
法1.数的小性质：首先，我们把36分解成可以被4和9整除

对于4的倍数只要看最后两位，对于9的倍数只要各个位上的数字和为9倍数。

假如有10个最后两位24，%9等于6的数，我们只要找%9==3的拼前面相乘即可。

我们用cnt[x][y]统计最后两位为x %9等于y的个数。

注意对于个位数，5和105是不一样的，若为105则直接抛弃，但是5的话还需要特判一下。

法2.模的性质：

我们把每一个数记录一下它%36以及它的位数。

我们先正着枚举一遍当前作为高位，前面作低位的情况，然后反着再来一遍使刚刚作高位的反过来作低位（这样可以避免自己加自己）。

下面是AC代码：

#include<bits/stdc++.h>
using namespace std;
long long n,sum[40];
struct node{
    long long zhi;
    int cnt;
}a[100010];
int cc(long long ck){
    int ccc=0;
    while(ck){
        ck/=10;
        ccc++;
    }
    return ccc;
}
long long qpow(long long a,long long b){
    long long ans = 1;
    while(b)
    {
        if(b&1) ans = ans * a;
        b >>= 1;
        a = a * a;
    }
    return ans%36;
}
int main(){
    cin>>n;
    for(int i=1;i<=n;i++){
        scanf("%lld",&a[i].zhi);
        a[i].cnt=cc(a[i].zhi);
        a[i].zhi=a[i].zhi%36;
    }
    long long sss=0;
    for(int i=1;i<=n;i++){
        for(int j=0;j<36;j++){
            if((a[i].zhi+j*qpow(10,a[i].cnt))%36==0) sss+=sum[j];
        }
        sum[a[i].zhi]++;
    }
    memset(sum,0,sizeof(sum));
    for(int i=n;i>=1;i--){
        for(int j=0;j<36;j++){
            if((a[i].zhi+j*qpow(10,a[i].cnt))%36==0) sss+=sum[j];
        }
        sum[a[i].zhi]++;
    }
    cout<<sss;
}

3.枚举

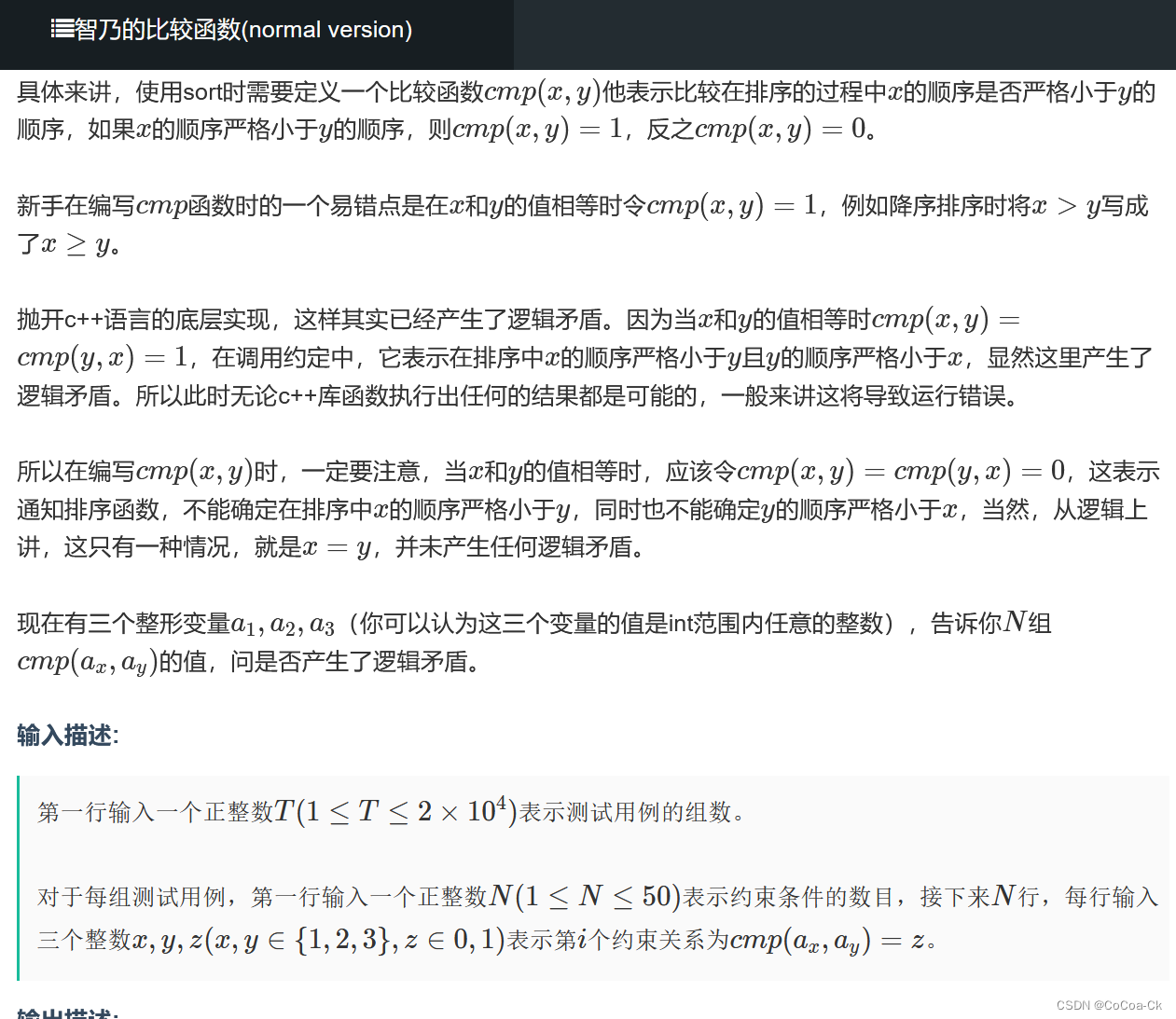
直接按照要求比较难写，但是总共就3个数，于是我们可以先用123枚举这3个数，然后判断即可。

下面是AC代码：

#include<bits/stdc++.h>
using namespace std;
int t,n,f;
struct node{
    int x,y,z;
}a[55];
int check(int a1,int a2,int a3){
    for(int i=1;i<=n;i++){
        if(a[i].z==0){
            if(a[i].x==1&&a[i].y==2&&a1<a2) return 0;
            if(a[i].x==1&&a[i].y==3&&a1<a3) return 0;    
            if(a[i].x==2&&a[i].y==1&&a2<a1) return 0;
            if(a[i].x==2&&a[i].y==3&&a2<a3) return 0;
            if(a[i].x==3&&a[i].y==1&&a3<a1) return 0;
            if(a[i].x==3&&a[i].y==2&&a3<a2) return 0;
        }
        else{
        if(a[i].x==a[i].y) return 0;
        if(a[i].x==1&&a[i].y==2&&a1>=a2) return 0;
        if(a[i].x==1&&a[i].y==3&&a1>=a3) return 0;    
        if(a[i].x==2&&a[i].y==1&&a2>=a1) return 0;
        if(a[i].x==2&&a[i].y==3&&a2>=a3) return 0;
        if(a[i].x==3&&a[i].y==1&&a3>=a1) return 0;
        if(a[i].x==3&&a[i].y==2&&a3>=a2) return 0;
        }
    }
    return 1;
}
int main(){
    cin>>t;
    while(t--){
        cin>>n;
        f=0;
        for(int i=1;i<=n;i++){
            scanf("%d%d%d",&a[i].x,&a[i].y,&a[i].z);
        }
        for(int i=1;i<=3;i++){
            for(int j=1;j<=3;j++){
                for(int w=1;w<=3;w++){
                    if(f==1) continue;
                    if(check(i,j,w)){
                        f=1;
                    }
                }
            }
        }
        if(!f) cout<<"No"<<endl;
        else cout<<"Yes"<<endl;
    }
}

4.高中概率题：

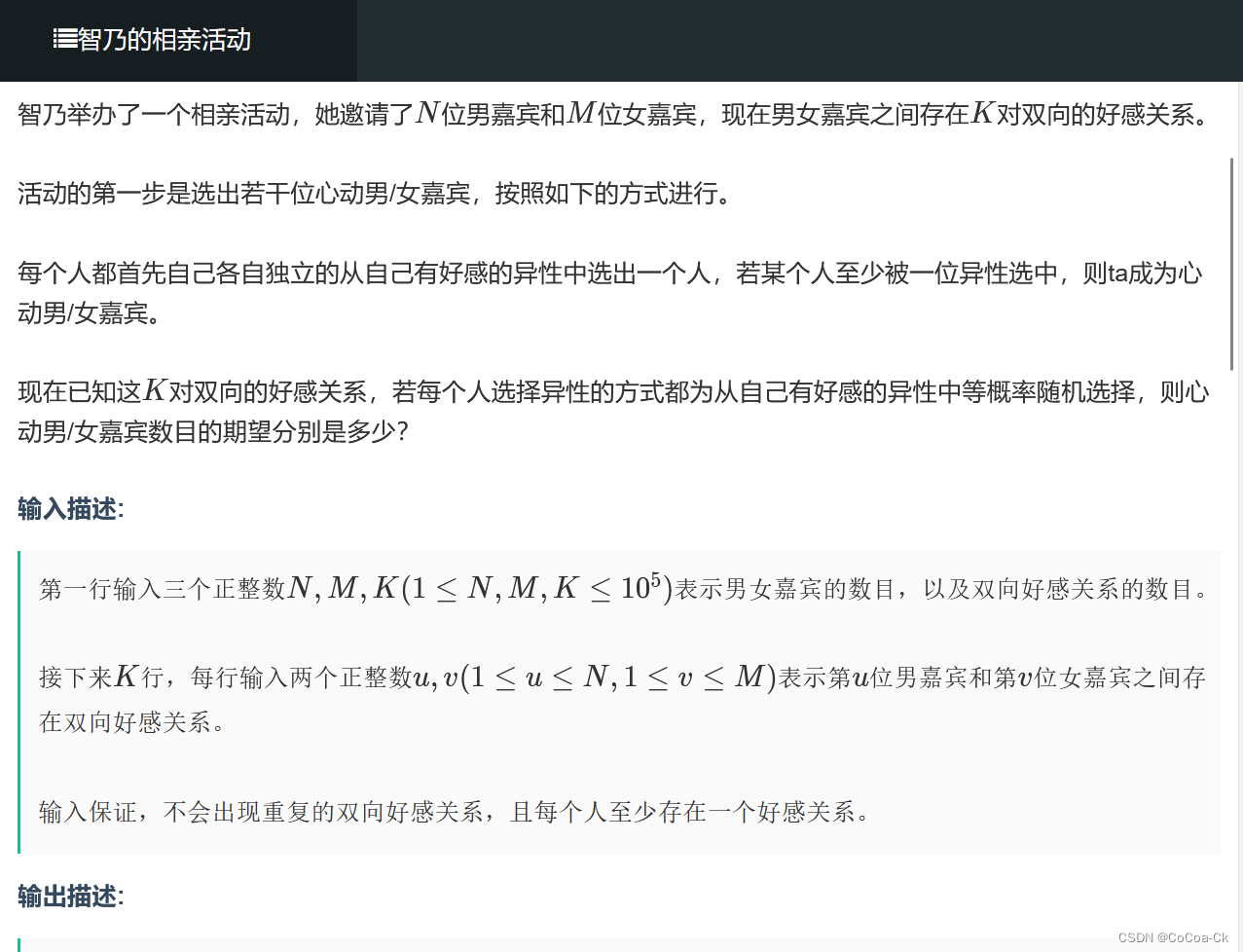
直接算比较麻烦，我们对于每一个人，我们不妨计算它不被选的p

- $p=1-\prod (1-1/ei)$ ,然后加起来即可。

#include<bits/stdc++.h>
using namespace std;
int n,m,k,u,v;
double p1[100010],p2[100010];
vector<int> b1[100010],b2[100010];
int main(){
    cin>>n>>m>>k;
    for(int i=1;i<=n;i++) p1[i]=1;
    for(int i=1;i<=m;i++) p2[i]=1;
    for(int i=1;i<=k;i++){
        scanf("%d%d",&u,&v);
        b1[u].push_back(v);
        b2[v].push_back(u);
    }
    for(int i=1;i<=n;i++){
        double k=b1[i].size();
        for(int j=0;j<b1[i].size();j++){
            p2[b1[i][j]]*=(k-1)/k;
        }
    }
    for(int i=1;i<=m;i++){
        double k=b2[i].size();
        for(int j=0;j<b2[i].size();j++){
            p1[b2[i][j]]*=(k-1)/k;
        }
    }
    double ans1=0,ans2=0;
    for(int i=1;i<=n;i++) ans1+=1-p1[i];
    for(int i=1;i<=m;i++) ans2+=1-p2[i];
    cout<<"float"<<endl;
    printf("%.10f %.10f",ans1,ans2);
}

5.模拟题：

显然，只要黑色节点为奇数，红色节点为偶数，并且保证黑色节点数不超过红色节点数*2+1，红色节点数不超过黑色节点数*2即可。

至于构造，我们只要构建一个完全二叉树，每一层红黑相间即可。

我们可以用BFS的思想来层序遍历即可，下面是AC代码：

#include<bits/stdc++.h>
using namespace std;
int t,cnt,a,b;
queue<int> q;
int main(){
    cin>>t;
    while(t--){
        cnt=2;
        while(!q.empty()) q.pop();
        scanf("%d%d",&a,&b);
        if(a%2==0||b%2==1||a>2*b+1||b>2*a) cout<<"No"<<endl;
        else{
            a--;
            cout<<"Yes"<<endl;
            q.push(1);
            while(!q.empty()){
                int ck=q.front();
                q.pop();
                if(ck==1){
                    if(b==0) cout<<-1<<" "<<-1<<endl;
                    else{
                        cout<<cnt<<" "<<cnt+1<<endl;
                        cnt+=2;
                        q.push(0);
                        q.push(0);
                        b-=2;
                    }
                }
                else{
                     if(a==0) cout<<-1<<" "<<-1<<endl;
                    else{
                         cout<<cnt<<" "<<cnt+1<<endl;
                        cnt+=2;
                        q.push(1);
                        q.push(1);
                        a-=2;
                    }
                }
            }
        }
    }
}

6。DP（目前感觉最难也最巧的）

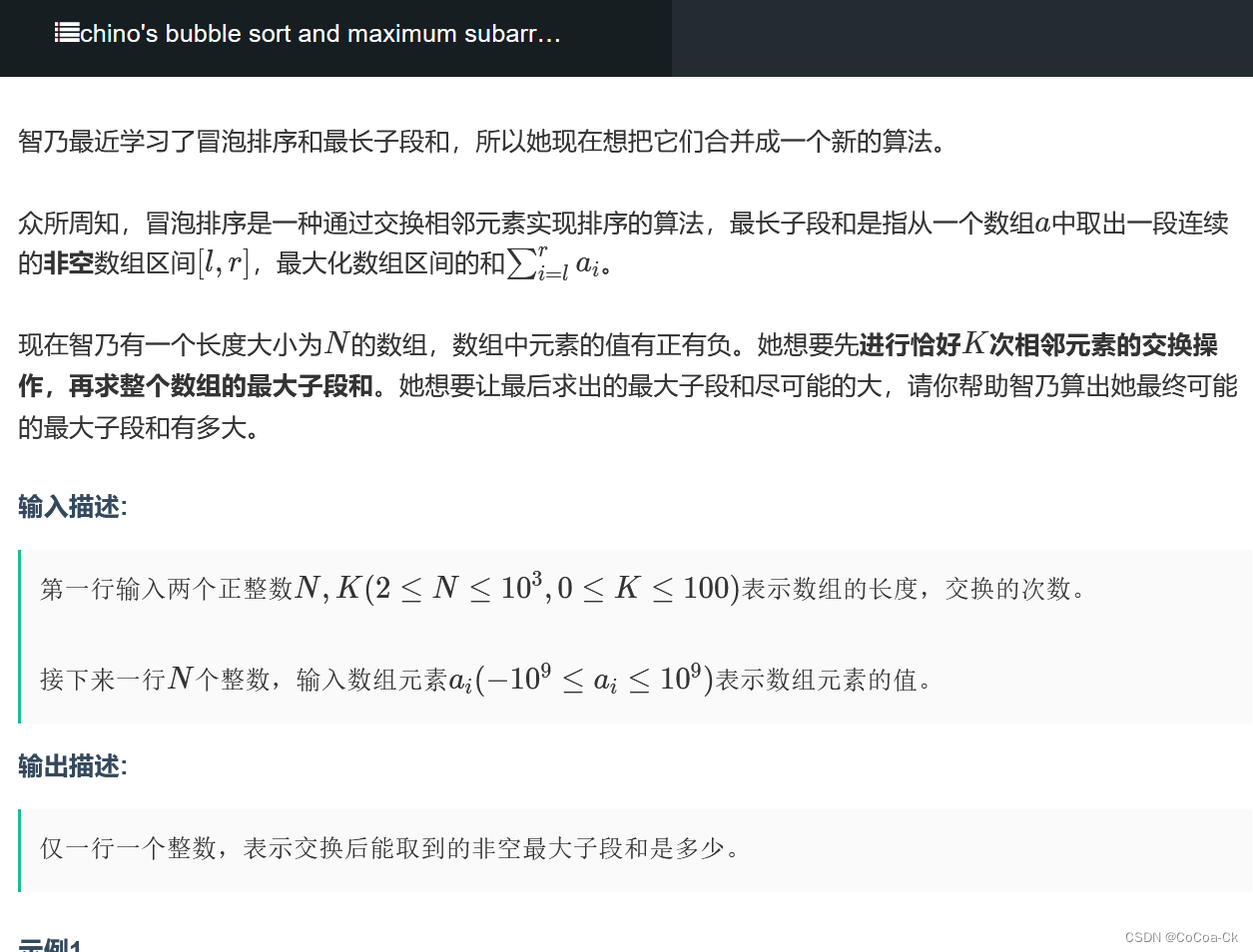
比较地妙，我们假如在最终答案时让1表示选，0表示不选，那么对于111101001，只要把0移走的次数小于交换次数就是可以的，其中我们要把0移走，那么怎么移呢？

它可以往左移也可以往右移，而假如一个元素往左移了，它左边的0一定也要左移，因此一定存在一个分界线，它左边的0都左移，它右边的都右移。于是我们枚举断点，那么答案就是这两端的拼接。

但是又有一个问题，那就是我们怎么知道一个数选还是不选？

我们不妨令dp[i][j][k]表示前i个数字已经处理过，其中要移j次，k为保留的个数（其实是一个动态的0/1背包，这里的V不能直接确定，于是增加一个维度来处理）。

易得dp[i][j][k]=max(dp[i-1][j][k-1]+a[i],dp[i-1][j-k][k])。

那么如何拼接？当dp完成后，其保留的个数没有用了，于是我们令f[i][j]表示1--i交了j次，那么答案是单个元素或者fl[i][j]+fr[i+1][w]。

下面是AC代码：

#include<bits/stdc++.h>
using namespace std;
long long n,k,dp1[110][1010],dp2[110][1010],a[1010],fl[1010][110],fr[1010][110];
int main(){
    cin>>n>>k;
    for(int i=1;i<=n;i++) scanf("%lld",&a[i]);
    memset(dp1,-0x3f,sizeof(dp1));
    memset(dp2,-0x3f,sizeof(dp2));
    memset(fl,-0x3f,sizeof(fl));
    memset(fr,-0x3f,sizeof(fr));
    dp1[0][0]=0,dp2[0][0]=0;
    for(int i=1;i<=n;i++){
        for(int j=k;j>=0;j--){
            for(int w=n;w>=1;w--){
                long long res=-1e18;
                res=max(res,dp1[j][w-1]+a[i]);
                if(j-w>=0) res=max(res,dp1[j-w][w]);
                dp1[j][w]=res;
                fl[i][j]=max(fl[i][j],dp1[j][w]);
            }
        }
    }
    for(int i=n;i>=1;i--){
        for(int j=k;j>=0;j--){
            for(int w=n;w>=1;w--){
                long long res=-1e18;
                res=max(res,dp2[j][w-1]+a[i]);
                if(j-w>=0) res=max(res,dp2[j-w][w]);
                dp2[j][w]=res;
                fr[i][j]=max(fr[i][j],dp2[j][w]);
            }
        }
    }
    long long ans=-1e18;
    for(int i=1;i<=n;i++) ans=max(ans,a[i]);
    for(int i=1;i<=n;i++){
        for(int j=0;j<=k;j++){
            for(int jj=0;jj<=k;jj++){
                if(j+jj<=k){
                    ans=max(ans,fl[i][j]+fr[i+1][jj]);
                }
            }
        }
    }
    cout<<ans;
}