垃圾小白羊leetcode刷题记录2

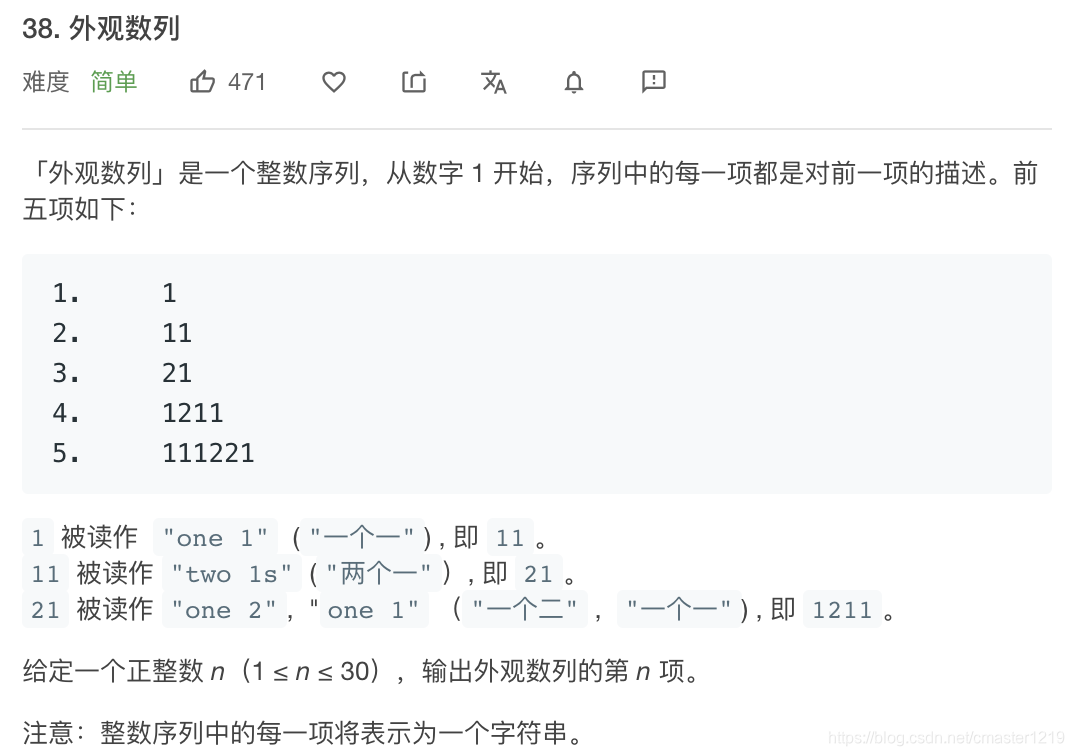
我的解法：

class Solution:
    def countAndSay(self, n: int) -> str:
        if n == 1:
            return "1"
        i = 1
        obj = self.countAndSay(n-1)
        val = obj[0]
        count = 1
        res = ''
        while i < len(obj):
            if obj[i] != val:
                res += (str(count)+val)
                val = obj[i]
                count = 1
            else:
                count += 1
            i += 1
        res += (str(count)+val)
        return res

采用递归算法，n=1时作为基本样例，对其余的输入n，以countAndSay(n-1)作为描述对象，遍历该描述对象，记录当前的数字以及其对应的连续出现次数，若数字改变，则将之前的数字及次数记录到结果中，重新开始计数。

---

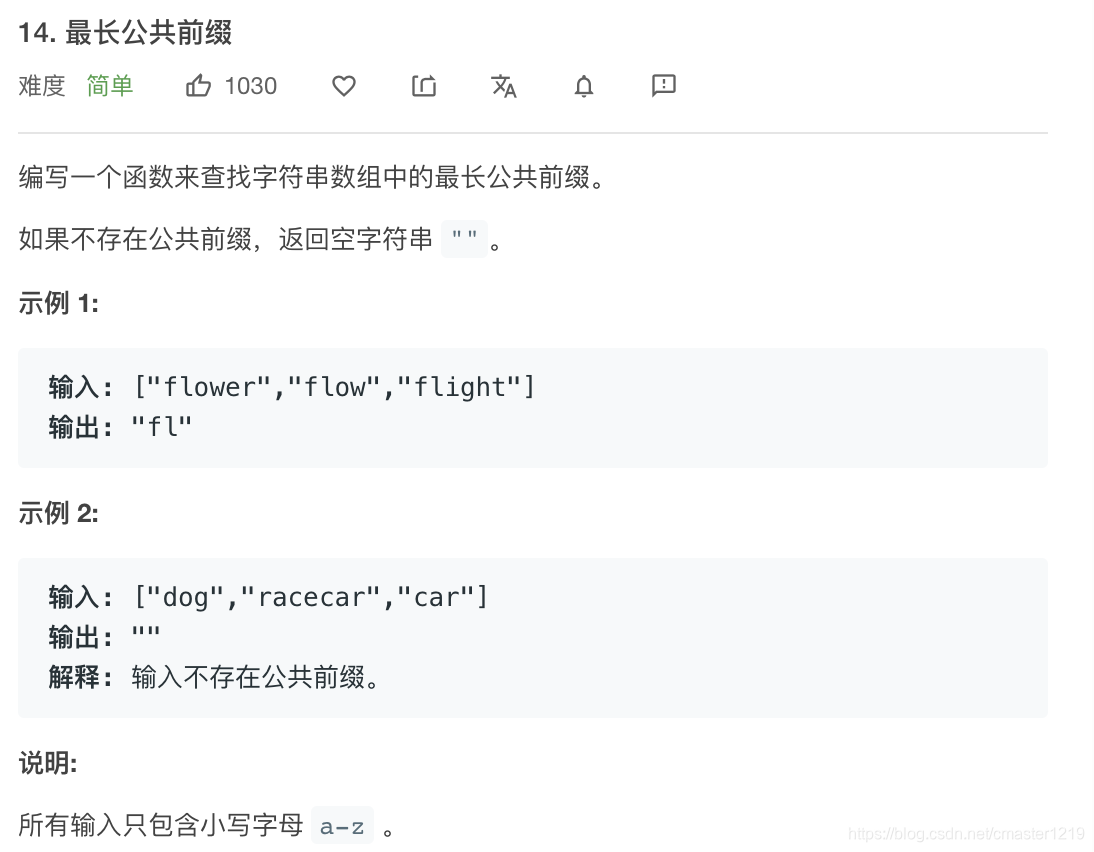
我的解法：

class Solution:
    def longestCommonPrefix(self, strs: List[str]) -> str:
        if not strs:
            return ""
        min_len = min(map(len,strs))
        if min_len == 0:
            return ""
        for i in range(min_len, 0, -1):
            if len(set(map(lambda x: x[:i],strs))) == 1:
                return strs[0][:i]
        return ""

首先判断列表是否为空或有空元素，若有直接返回""，之后找到列表中最短的字符串，以它的长度min_len开始判断公共前缀长度，通过判断列表各元素前i位组成的集合长度是否为1来确定各元素是否有公共前缀。最后若第一位元素都不相同，则返回""。

---

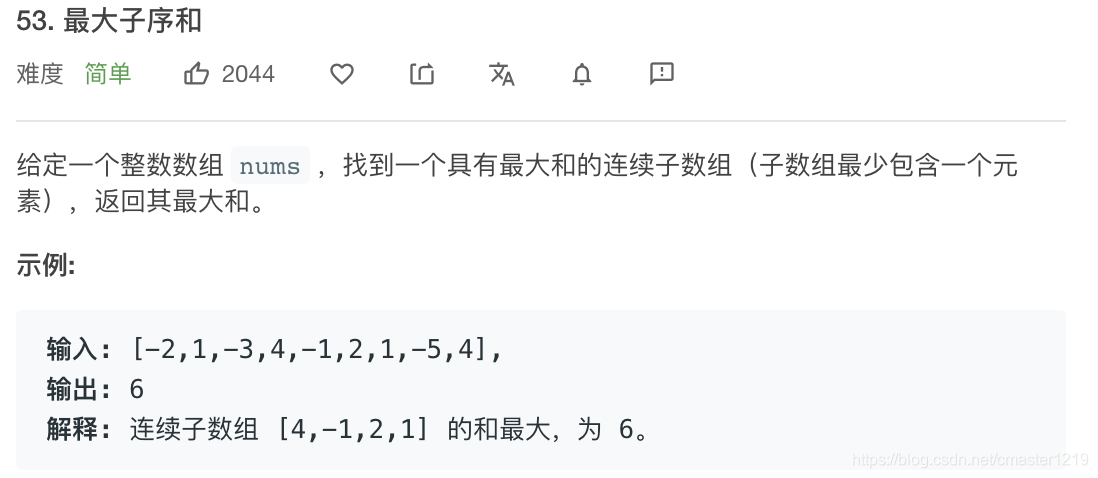
我的解法：

class Solution:
    def maxSubArray(self, nums: List[int]) -> int:
        tmp = nums[0]
        max_ = tmp
        for i in range(1, len(nums)):
            if tmp >= 0:
                max_ = max([nums[i]+tmp, tmp, max_])
                tmp += nums[i]
    
            else:
                max_ = max([tmp, nums[i], max_])
                tmp = nums[i]
        return max([max_, tmp])

遍历一边数列，记录当前累加和以及最大值。若前项累加和大等于0，则继续累加；若前项累加和小于0，则以当前元素为起点重新开始累加。途中不断记录更新最大值。

大佬解法：

class Solution:
    def maxSubArray(self, nums: List[int]) -> int:
        n = len(nums)
        if n == 1:
            return nums[0]
        max_left = self.maxSubArray(nums[:n//2])
        max_right = self.maxSubArray(nums[n//2:])

        tmp = 0
        max_l = nums[n//2-1]
        for i in range(n//2-1,-1,-1):
            tmp += nums[i]
            max_l = max([tmp, max_l])

        tmp = 0
        max_r = nums[n//2]
        for i in range(n//2,n):
            tmp += nums[i]
            max_r = max([tmp, max_r])
        return max([max_left, max_right, max_l+max_r])

使用分治法，将数列等分为左边和右边两部分，最大子序和可能产生于左数列、右数列或者中间，分别计算三者的最大子序和，其中最大者为原序列的最大子序和。左右数列的最大子序和可以由递归求得，中间序列的最大子序和分左右两半求得，左半部分由右向左遍历累加，只需考虑累加中的最大值，同理右半部分考虑从左向右遍历累加中的最大值，左右半边之和几位中间序列的最大子序和。

---

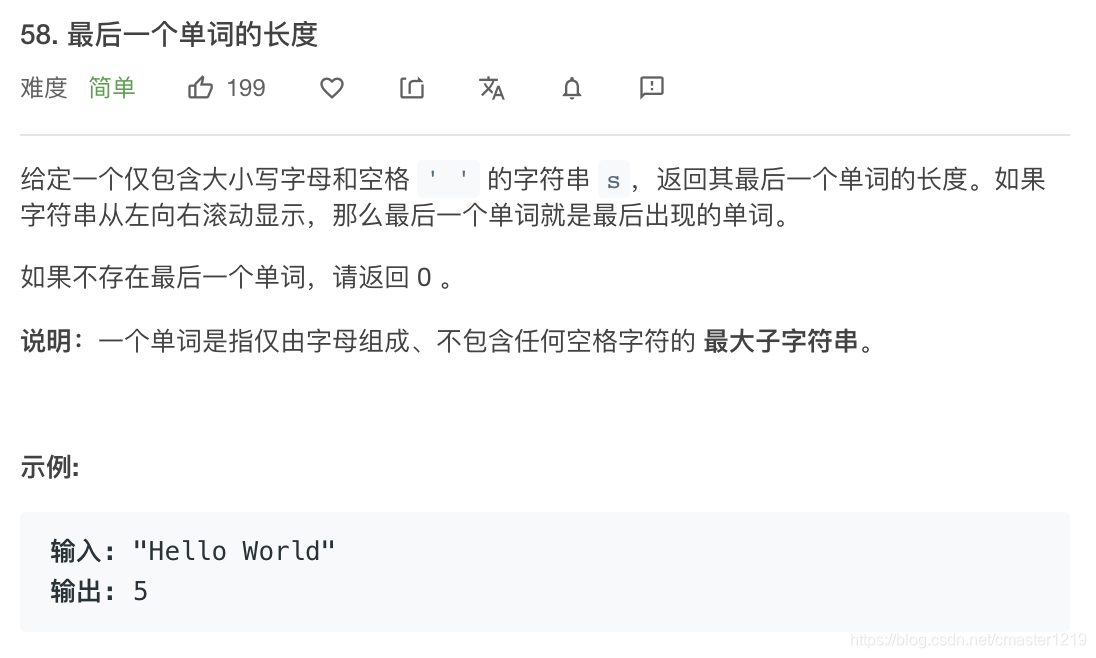
我的解法：

class Solution:
    def lengthOfLastWord(self, s: str) -> int:
        n = len(s.rstrip())
        if n == 0:
            return 0
        for i in range(n-1, -1, -1):
            if s[i] == ' ':
                return n-i-1
        return n

删除字符串末尾的空格" "，从后往前计数，遇到第一个空格时输出当前计数。

---

我的解法：

class Solution:
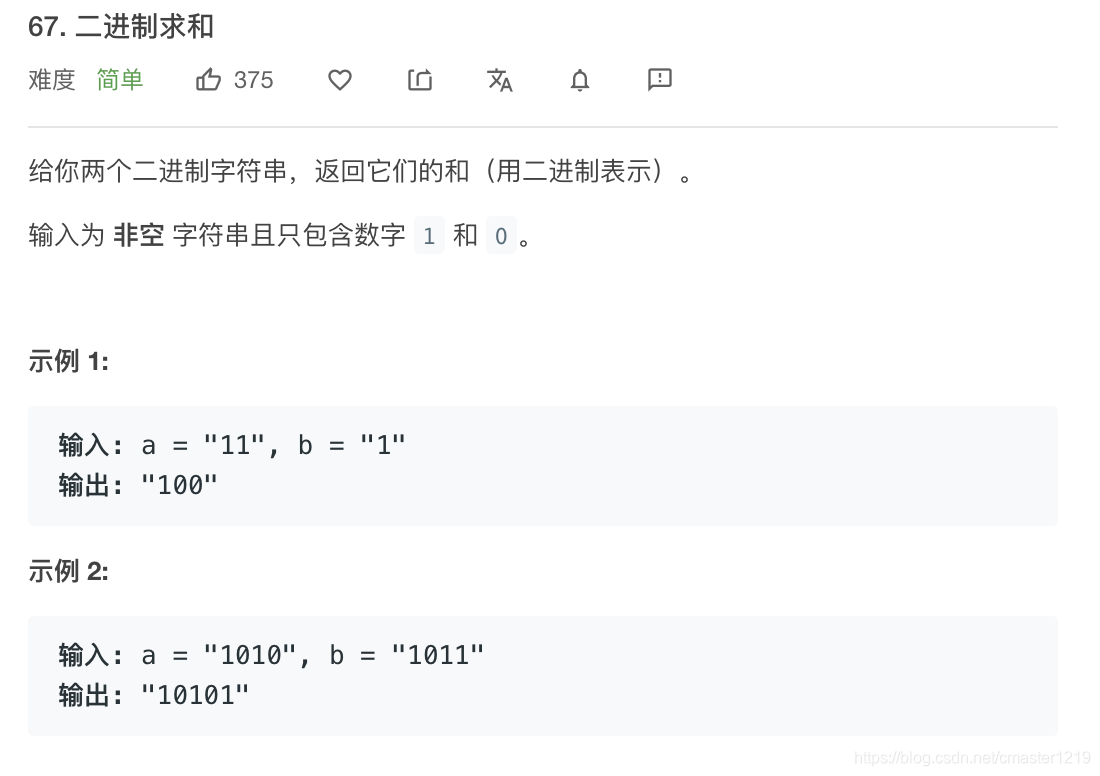
    def addBinary(self, a: str, b: str) -> str:
        sum = list(str(int(a)+int(b)))
        for i in range(len(sum)-1, -1, -1):
            if int(sum[i]) >= 2:
                sum[i] = str(int(sum[i])-2)
                if i>0:
                    sum[i-1] = str(int(sum[i-1])+1)
                else:
                    sum.insert(0,'1')
        return ''.join(sum)

将两二进制字符串转为整数后相加，由后往前遍历，若出现大等于2的项，则该项减一，前项加一，遍历至首项后，若首项大等于2，则在加和项最前面插入1。

大佬解法：

class Solution:
    def addBinary(self, a: str, b: str) -> str:
        a, b = int(a,2), int(b,2)
        while b:
            answer = a ^ b
            carry = (a & b) << 1
            a, b = answer, carry
        return bin(a)[2:]

使用位运算，将两者加和分解为无进位相加结果，以及进位部分。前者由两二进制数异或运算获得，后者由两者与运算再左移一位获得。两者视为新的两个二进制数，继续做加和，直至进位部分为0为止。

---

我的解法：

class Solution:
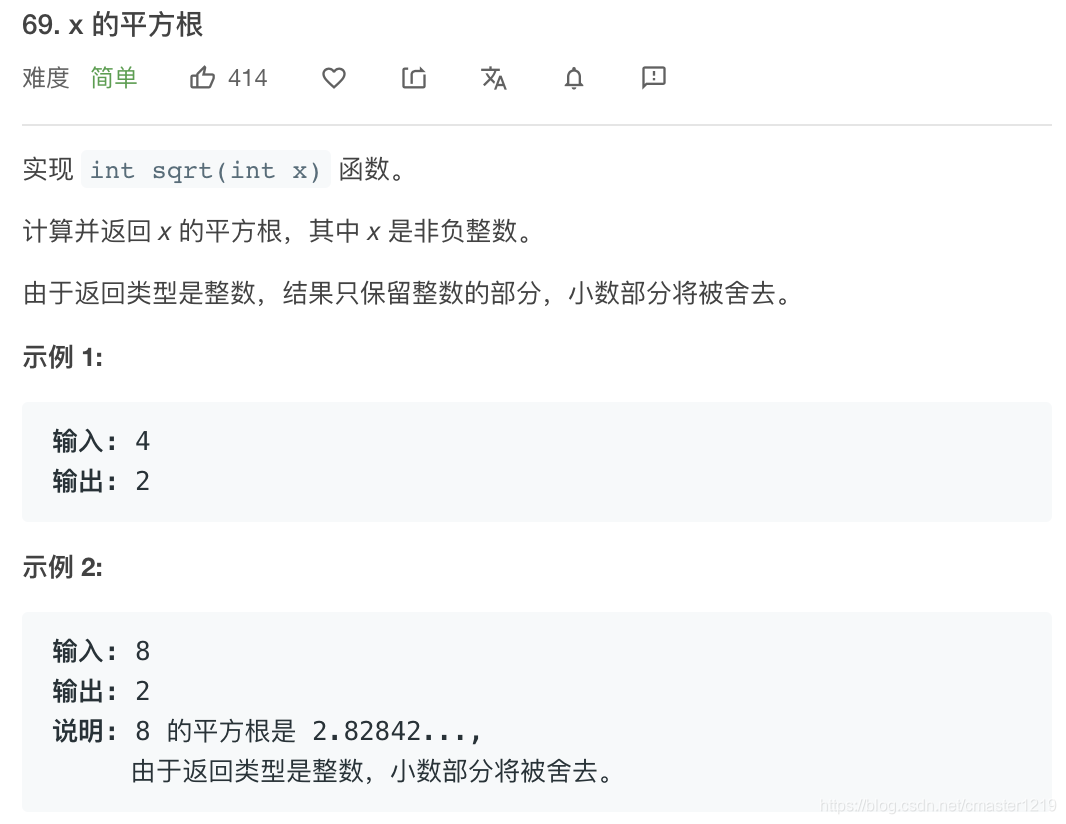
    def mySqrt(self, x: int) -> int:
        l, r, ans = 0, x, -1
        while r >= l:
            mid = (l+r)//2
            if x == mid**2:
                return mid
            elif x > mid**2:
                ans = mid
                l = mid+1
            else:
                r = mid-1
        return ans

二分法查找，初始范围是[0, x]。

---

我的解法：

class Solution:
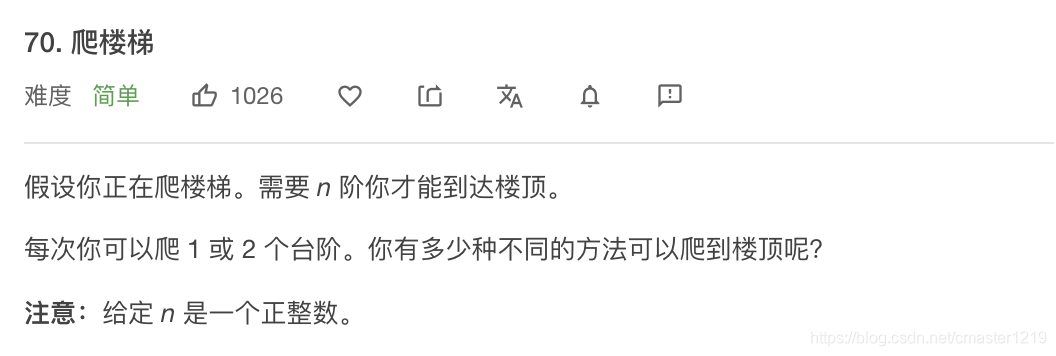
    def climbStairs(self, n: int) -> int:
        memo = {1:1, 2:2}

        def fn(n):
            if memo.get(n):
                return memo.get(n)

            else:
                ans = memo.get(n-1, fn(n-1)) + memo.get(n-2, fn(n-2))
                memo[n] = ans
                return ans
        
        return fn(n)

采用记忆化递归算法，用字典保存计算过的n对应的走法数fn(n)，以便接下来的递归过程中直接调用，时间复杂度O(n)。

大佬解法：

class Solution:
    def climbStairs(self, n: int) -> int:
        if n == 1:
            return 1
        if n == 2:
            return 2

        fir = 1
        sec = 2
        for i in range(n-2):
            thr = fir+sec
            fir = sec
            sec = thr
        return thr

动态规划思想，运用f(n) = f(n-1)+f(n-2)的子问题关系式，循环n-2次计算n级台阶对应的取值，每次只记录更新f(n-1)和f(n-2)，时间复杂度O(n)。

---

我的解法：

# Definition for singly-linked list.
# class ListNode:
#     def __init__(self, x):
#         self.val = x
#         self.next = None

class Solution:
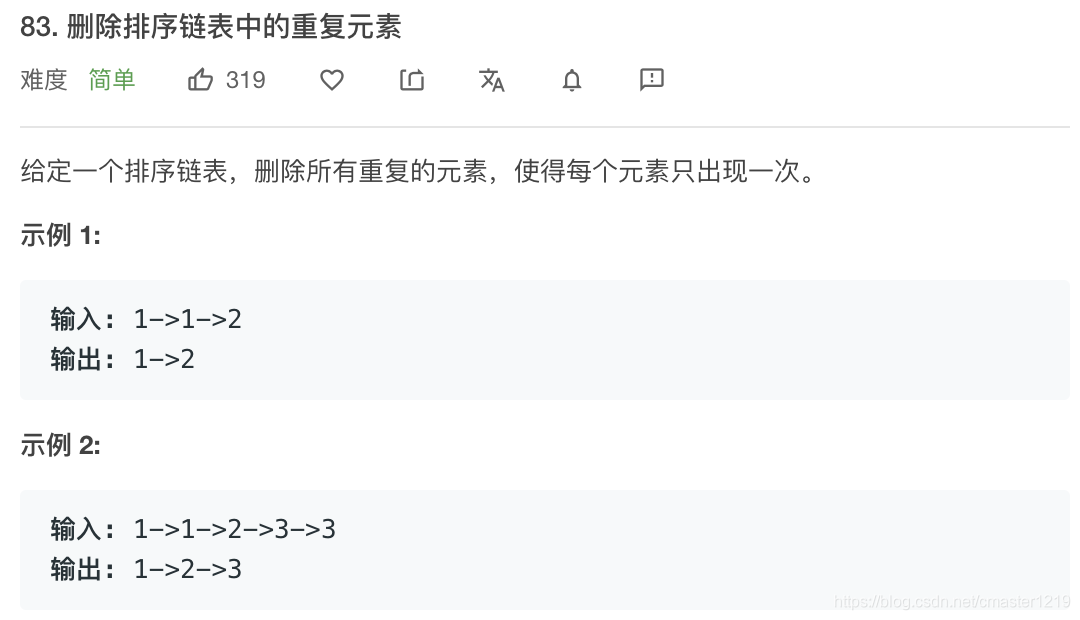
    def deleteDuplicates(self, head: ListNode) -> ListNode:
        if not head:
            return 
        fir = head
        sec = head.next
        while sec:
            if sec.val == fir.val:
                sec = sec.next
                fir.next = None
            else:
                fir.next = sec
                fir = sec
                sec = sec.next
        return head

双指针，如果两个指针的值相等，第一个指针指向第二个指针的后一位。

另有解法：

# Definition for singly-linked list.
# class ListNode:
#     def __init__(self, x):
#         self.val = x
#         self.next = None

class Solution:
    def deleteDuplicates(self, head: ListNode) -> ListNode:
        if not head:
            return 
        child = self.deleteDuplicates(head.next)
        if child and (head.val == child.val):
            head.next = child.next

        return head

递归算法，将链表递归的分为首位元素以及剩余子链表，对于剩余的子链表递归调用原函数，比较子链表返回结果首位与父链表首位元素，若相同，则父链表首元素指向子链表第二位元素。

---

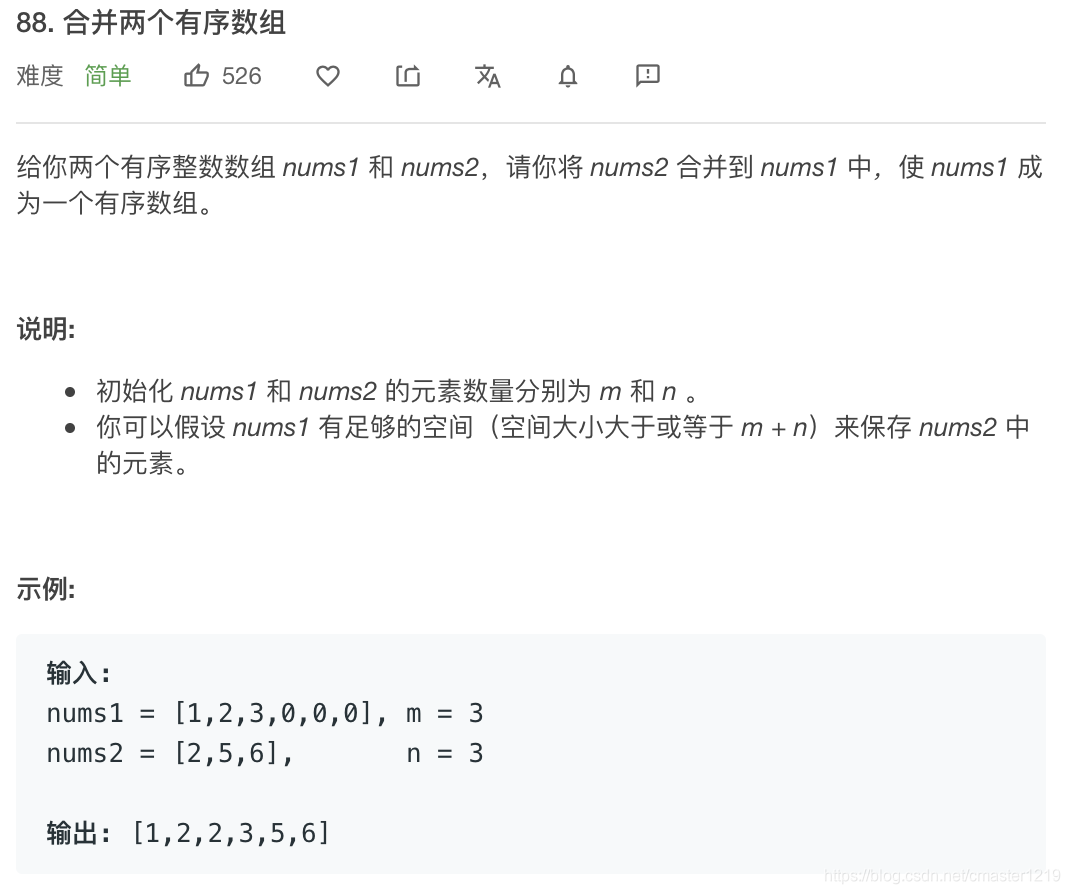
我的解法：

class Solution:
    def merge(self, nums1: List[int], m: int, nums2: List[int], n: int) -> None:
        """
        Do not return anything, modify nums1 in-place instead.
        """
        i, j, t = m-1, n-1, m+n-1
        if nums2:
            while t>=0:
                if nums1[i] <= nums2[j]:
                    nums1[t] = nums2[j]
                    j -= 1
                else:
                    nums1[t] = nums1[i]
                    i -= 1
                t -= 1
                
                if j < 0:
                    break
                if i < 0:
                    nums1[:j+1] = nums2[:j+1]
                    break

特别考虑避免出现插入操作，降低时间复杂度。采用反向遍历三指针方法，指针i、j分别指向两数组的尾部，主指针t从nums1的m+n-1元素开始反向遍历，取值为指针i、j指向元素的较大值。当nums2遍历完成时，直接结束遍历；当nums1遍历完成时，将nums1的前j个元素替换为nums2的前j个元素。

---