边缘分布和条件分布

最新推荐文章于 2025-11-25 00:00:00 发布
原创 最新推荐文章于 2025-11-25 00:00:00 发布 · 3.2k 阅读 · 18 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
文章标签：

#概率论

本文介绍了概率论和统计学中的边缘分布和条件分布，边缘分布关注单个变量的独立分布，通过求和或积分获得；条件分布则关注在已知其他变量的情况下，某个变量的概率分布。

边缘分布（Marginal Distribution）和条件分布（Conditional Distribution）是概率论和统计学中两个重要的概念。

边缘分布（Marginal Distribution）： 边缘分布是指在多维随机变量的联合分布中，对其中某一个或某几个变量的分布。具体而言，如果有一个二维随机变量 (X, Y) 的联合分布，那么X的边缘分布就是在所有可能的Y值上对联合分布进行求和或积分，得到X的分布。同理，Y的边缘分布是在所有可能的X值上对联合分布进行求和或积分，得到Y的分布。

数学表达：

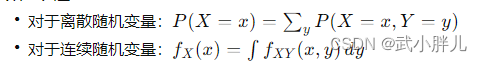
条件分布（Conditional Distribution）： 条件分布是在给定另一随机变量或一组随机变量的条件下，某个随机变量的分布。在条件分布中，我们关心的是在某种条件下的随机变量的行为。

数学表达：

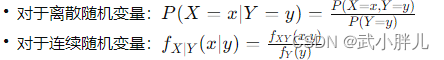
在这些公式中，P(X=x,Y=y) 表示X和Y同时取特定值的联合概率（离散情况下），fXY​(x,y) 表示X和Y的联合概率密度函数（连续情况下），而  P(Y=y) 或 fY​(y) 表示边缘分布。

总的来说，边缘分布关注单个变量的分布，而条件分布关注在给定其他变量的条件下某个特定变量的分布

图解联合概率密度、边缘概率密度、条件概率密度之间的关系
一个搬运知识的笨小孩
10-12 2万+
简要图解联合概率密度、边缘概率密度、条件概率密度之间的关系
联合分布、边缘分布、条件分布各函数之间的关系
一个搬运知识的笨小孩
05-21 5992
联合分布、边缘分布、条件分布各函数之间的关系
CS229《机器学习》笔记 | 多元高斯分布的边缘分布和条件分布
X的博客
12-15 8724
吴恩达的《机器学习（CS229）》Lecture note 9（Part X Factor analysis）中提及了多元高斯分布的边缘分布和条件分布，指出这两者本身亦是高斯分布，但没有给出详细的证明。我自己尝试着推导，但不得要领，直到上网搜索后才恍然大悟。现将该证明过程记录于此，关键在于对协方差矩阵进行LDU分解。 边缘分布 一个多元概率分布的部分元所服从的概率分布即边缘分布，通过将剩余元求...
边际分布与条件分布函数；条件概率和条件密度；随机变量的独立性；随机向量简单函数的分布
最新发布
BLOG域名:programb.blog.youkuaiyun.com
11-25 72
| 边际密度 | $ f_X(x) = \int f(x,y)\,dy $ | | 条件密度 | $ f_{X|Y}(x|y) = \frac{f(x,y)}{f_Y(y)} $ | | 独立性判定 | $ f(x,y) = f_X(x)f_Y(y) $ | | 和的密度（独立） | $ f_{X+Y}(z) = \int f_X(x)f_Y(z-x)\,dx $ | | 最大值分布（独立） | $ F_{\max} = F_X(z)F_Y(z) $ | | 商的密度（独立） | $ f_{X/Y}(z)
机器学习|条件分布（离散型、连续型随机变量）|10mins入门|概统学习笔记（四）
用途：中英文学习笔记，如有侵权，可评论留言，及时清理；学历：NUS计算机硕士；SYSU地球物理学士
03-28 2815
条件分布 背景：在事件B发生的条件下事件A发生的条件概率： P(A∣B)=P(AB)P(B) P(A|B)=\frac{P(AB)}{P(B)} P(A∣B)=P(B)P(AB)​ 随机变量条件分布：设有两个随机变量X，Y，在给定Y取某个或某些值的条件下，求X的概率分布 条件分布是一种概率分布，它具有概率分布的一切性质，正如条件概率是一种概率，具有概率的一切性质 例如： P(X=xi...
【概率论】3-5:边缘分布(Marginal Distribution)
热门推荐
Tony的博客
09-22 1万+
title: 【概率论】3-5:边缘分布(Marginal Distribution) categories: Mathematic Probability keywords: Marginal p.f. 边缘概率函数 Marginal p.d.f. 边缘密度函数 Independent 独立性 toc: true date: 2018-02-09 11:33:45 Abstract: 本...
Marginal distribution
weixin_33754913的博客
08-12 192
http://www.ask.com/wiki/Marginal_probability   Real-world example Imagine for example you want to compute the probability that a pedestrian will be hit by a car while crossing the road at a pedestr...
对齐边际分布和条件分布
qq_51465769的博客
12-07 857
对齐边际分布和条件分布
多元高斯分布的边际分布与条件分布
03-30
在多元高斯分布中，边际分布和条件分布是研究多个变量相互依赖关系的重要工具。 边际分布是指从多元分布中获得单个变量或变量子集的概率分布。例如，假设有一个n维随机向量X，其可以被分割为两个子向量Y和Z，维度...
PRML学习笔记-条件高斯分布与边缘高斯分布的常用性质
qq_37394299的博客
11-14 1315
条件高斯分布与边缘高斯分布的常用性质 基本知识 多元高斯分布的一个重要性质是,如果两组变量是联合高斯分布,那么以一组变量为条件,另一组变量同样是高斯分布。类似地,任何一个变量的边缘分布也是高斯分布。 首先考虑条件概率的情形。假设 x 是一个服从高斯分布 N(x∣μ,Σ)\mathcal{N}(\boldsymbol{x} | \boldsymbol{\mu}, \mathbf{\Sigma})N(...
深入理解边缘高斯分布与条件高斯分布
新型多传感器导航融合算法及基于贝叶斯框架下自适应鲁棒滤波
01-23 2853
多元高斯分布在统计学和机器学习领域中扮演着关键的角色。在这个分布的框架下，我们经常会遇到边缘高斯分布和条件高斯分布，它们分别涉及了从原始分布中选择一部分变量和在已知条件下计算其他变量的概率分布。本文将深入研究这两个概念，探讨它们的核心思想、数学表示以及在实际问题中的应用。
迁移学习在深度学习中的边缘分布对齐和条件分布对齐
lyy的博客
02-09 4296
个人理解： 边缘分布对齐：源数据和目标数据输入神经网络，经过卷积池化等操作提取特征后，形成的feature map相似。 条件分布对齐：不光要feature相似，还得是同类别的feature map相似，比如分类标签为1的源数据的feature map和分类标签为1的目标数据的feature map相似，而不是和分类标签为2或其他的目标数据的feature map相似。 注意，迁移学习的目的之一是为少标签的数据添加标签，所以训练的时候不能使用目标数据的标签，这样限制了我们的操作空间、操作手段，高精度还是挺.
迁移学习中的条件概率分布与边缘概率分布
小帆的博客
11-10 6934
在迁移学习中，一个热门的研究方向是领域自适应（Domain Adaptation）。在领域自适应的定义中，涉及到条件概率分布与边缘概率分布，先就其定义解释如下。 首先定义联合概率。假设有随机变量X与Y，此时P(X=a, Y=b)用于表示X=a且Y=b的概率。这类包含多个条件且所有条件同时成立的概率称为联合概率。联合概率一览表被称为联合概率分布。 接下来定义边缘概率。边缘概率与联合概率相对应，当P(...
边缘分布
User
04-04 1万+
什么是边缘分布函数，有那些性质 设F(x,y)F(x,y)F(x,y)为随机变量(X,Y)(X,Y)(X,Y)的分布函数，则F(x,y)=P{X≤x,Y≤y}F(x,y)=P\{X \le x,Y \le y\}F(x,y)=P{X≤x,Y≤y} 令 y→∞y \rightarrow \inftyy→∞，称P(X≤x)=P(X≤x,Y<∞)=F(x,∞)P(X \le x)=P(X\le x,Y < \infty) = F(x,\infty)P(X≤x)=P(X≤x,Y<∞)=F(x,∞)
三种分布 （边缘 &amp;amp; 联合 &amp;amp; 条件）
qq_34722315的博客
03-09 1817
自己的理解：联合分布：观察变量大于等于2时出现的概念，即多种变量同时出现时的概率（上图例子是变量为离散的情况，也有连续的情况）。边际分布/边缘分布：（和“边缘”两个字本身没太大关系，因为是求和，在表格中往往将这种值放在margin（表头）的位置，所以叫margin distribution），可以大致理解为，多种变量出现时，某一变量出现的概率。（关于求和的说法，可以参看例子，其和相加一定为1）条件...
概率图模型(01): 概述 & 三种分布 （边缘 & 联合 & 条件）
mjiansun的专栏
06-28 1057
https://blog.youkuaiyun.com/thither_shore/article/details/52192553
【笔记】迁移学习中边缘概率分布和条件概率分布
weixin_45648030的博客
06-04 4142
迁移学习——域自适应迁移学习概述（Transfer Learning）在迁移学习中，边缘概率分布和条件概率分布有什么含义？ 学习域适应之前比较陌生的是在迁移学习中边缘概率分布和条件概率分布有什么含义？（参考王晋东大佬和一些知乎上的回答）......
边缘分布 条件分布 联合分布
07-08
在概率论中，**边缘分布**、**条件分布**和**联合分布**是描述多个随机变量之间关系的重要概念。它们分别从不同的角度刻画了随机变量之间的依赖结构。 ### 联合分布 联合分布描述两个或多个随机变量**共同取值的概率分布**。对于离散型随机变量 $ X $ 和 $ Y $，其联合分布可以用联合概率质量函数 $ P(X = x, Y = y) $ 来表示；对于连续型随机变量，则用联合概率密度函数 $ f_{X,Y}(x, y) $ 表示。 例如，在引用中提到的例子中，$ X $ 是掷骰子的结果（取值为 1 到 6），$ Y $ 是抛硬币的结果（0 或 1），则 $ P(X = 3, Y = 0) $ 就是二者联合分布中的一个具体概率值[^1]。 ### 边缘分布 边缘分布是指从联合分布中“提取”出单个随机变量的分布。它是通过对联合分布中另一个变量的所有可能取值进行求和（离散情况）或积分（连续情况）得到的。 对于离散变量，边缘分布律定义为： $$ p_i = \sum_{j=1}^{\infty} p_{ij},\quad i = 1,2,\cdots $$ 类似地，对另一个变量也存在对应的边缘分布： $$ p_j = \sum_{i=1}^{\infty} p_{ij},\quad j = 1,2,\cdots $$ 这些公式表明，边缘分布本质上是从联合分布中忽略其他变量信息后所保留的关于某个变量的概率分布[^3]。 ### 条件分布 条件分布描述的是在已知某一个变量取特定值的前提下，另一个变量的分布情况。它反映了变量之间的依赖关系。 对于离散变量，条件分布可以表示为： $$ P(X = x \mid Y = y) = \frac{P(X = x, Y = y)}{P(Y = y)} $$ 前提是 $ P(Y = y) > 0 $。同样地，也可以定义 $ P(Y = y \mid X = x) $。 在连续情况下，条件概率密度函数定义为： $$ f_{X|Y}(x \mid y) = \frac{f_{X,Y}(x, y)}{f_Y(y)} $$ 其中 $ f_Y(y) $ 是 $ Y $ 的边缘密度函数。 ### 区别与联系 - **区别**： - 联合分布描述的是多个变量**同时取值**的概率； - 边缘分布关注的是**单一变量**的概率分布，忽略其他变量； - 条件分布反映的是**在已知某一变量取值的前提下**，另一变量的分布情况。 - **联系**： - 联合分布可以通过边缘分布和条件分布相互转换： $$ P(X = x, Y = y) = P(X = x \mid Y = y) \cdot P(Y = y) $$ 这体现了乘法法则的基本思想[^2]。 - 边缘分布可以从联合分布中通过求和或积分获得； - 条件分布由联合分布和边缘分布共同决定。 ### 示例代码：计算联合分布下的边缘分布 以下是一个简单的 Python 示例，展示如何从二维离散联合分布中计算边缘分布： ```python import numpy as np # 假设有一个二维联合分布矩阵 P(X,Y)，行代表X，列代表Y joint_dist = np.array([ [0.1, 0.2], [0.3, 0.4] ]) # 计算X的边缘分布（按行求和） marginal_X = np.sum(joint_dist, axis=1) # 计算Y的边缘分布（按列求和） marginal_Y = np.sum(joint_dist, axis=0) print("X的边缘分布:", marginal_X) print("Y的边缘分布:", marginal_Y) ``` 该程序输出如下结果： ``` X的边缘分布: [0.3 0.7] Y的边缘分布: [0.4 0.6] ``` 这个例子展示了如何从联合分布中提取边缘分布，从而理解变量各自的独立分布特性。 ---
评论
成就一亿技术人!
拼手气红包6.0元
还能输入1000个字符
 
红包 添加红包
表情包 插入表情
表情包 代码片
 条评论被折叠 查看
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值