Partition
Time Limit: 6000/3000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)Total Submission(s): 422 Accepted Submission(s): 242
Problem Description
How many ways can the numbers 1 to 15 be added together to make 15? The technical term for what you are asking is the "number of partition" which is often called P(n). A partition of n is a collection of positive integers (not necessarily distinct) whose sum equals n.
Now, I will give you a number n, and please tell me P(n) mod 1000000007.
Now, I will give you a number n, and please tell me P(n) mod 1000000007.
Input
The first line contains a number T(1 ≤ T ≤ 100), which is the number of the case number. The next T lines, each line contains a number n(1 ≤ n ≤ 10
5) you need to consider.
Output
For each n, output P(n) in a single line.
Sample Input
4 5 11 15 19
Sample Output
7 56 176 490
思路:此题坑了,虽然很快想出了dp 的解法确发现根本开不了如此之大的数组。方法是:dp[n][k]代表k个数加起来等于n的种数。转移方程很容易dp[n][k]=dp[n-1][k-1]+dp[n-k][k]。本题正解用的是五边形数定理:(摘wiki百科里面的一段)
考虑 项的系数,在 n>0 时,等式右侧的系数均为0,比较等式二侧的系数,可得
项的系数,在 n>0 时,等式右侧的系数均为0,比较等式二侧的系数,可得
因此可得到分割函数p(n)的递归式
其中规律是两项两项的加减变化。然后里面是n-pi,其中pi是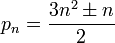 .其他细节可以看代码。
.其他细节可以看代码。
/*
* File :tmp.cpp
* Author :Kevin Tan
* Source :ZJNU
*
* 2013年8月7日,下午7:16:41
*/
#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<climits>
#include<utility>
#include<cctype>
#include<iomanip>
#include<string>
#include<map>
#include<deque>
#include<queue>
#include<set>
#include<vector>
#include<iterator>
using namespace std;
#define MAX 100005
#define MOD 1000000007
int q[MAX], p[MAX];
int main(int argc, char **argv) {
q[0] = 0;
int k = 1;
for (int i = 1; q[k - 1] <= MAX; i++) {
q[k++] = (3 * i * i - i) / 2;
q[k++] = (3 * i * i + i) / 2;
}
p[0] = 1;
for (int i = 1; i <= MAX; i++) {
p[i] = 0;
for (int j = 1; q[j] <= i; j++) {
if (((j - 1) >> 1) & 1) p[i] = (p[i] - p[i - q[j]]) % MOD;//(j-1)>>1 &1是符号两位两位的变
else p[i] = (p[i] + p[i - q[j]]) % MOD;
if (p[i] < 0) p[i] += MOD;
}
}
int T;
scanf("%d", &T);
while (T--) {
int n;
scanf("%d", &n);
printf("%d\n", p[n]);
}
return 0;
}







 本文探讨了一种利用五边形数定理解决整数分拆问题的高效算法,并提供了具体的实现代码,旨在帮助读者理解如何计算给定整数n的所有可能分拆方式的数量。
本文探讨了一种利用五边形数定理解决整数分拆问题的高效算法,并提供了具体的实现代码,旨在帮助读者理解如何计算给定整数n的所有可能分拆方式的数量。
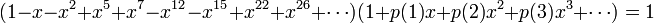
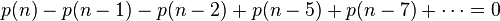

















 133
133

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








