推荐系统的多样性

背景

如果是用 point-wise 的方法, 根据ctr做倒排, 会出现 high similar items were clustered together 的现象. 相似的item扎堆, 这种体验并不友好.

MMR

Maximal Marginal Relevance .

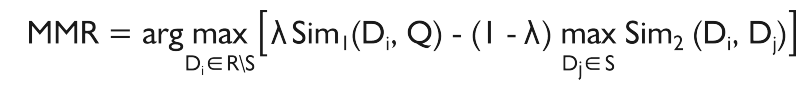
详见参考[2].
大致思想: 给定一个Query, 召回了一些文档A. 要从集合A中选一个大小为k的子集$A_k$ 呈现给用户. 每挑选一个元素i时, 综合考虑$A_k$ 的多样性和与Query相关性.

submodular diversification

思想

对$A_k$的评分函数为:
$$\rho (A_k)=\alpha \times d(A_k)+(1-\alpha )\sum _{a_i\in A_k}s(a_i)\text{\hspace{1em}(1)}$$
where $A_k$ is a subset of $A$ of size k.
$s(a)$ means the relevance between item $a$ and the current customer.
$d(A_k)$ is the measure of the diversity of $A_k$.
the optimal subset is given by:
$$A_k^{\ast }:=\underset{A_k\in A,|A_k|=k}{\mathrm{argmax}}\rho (A_k)\text{\hspace{1em}(2)}$$

落地

给出多样性的具体描述:
$$d(A_k)=\sum _i^k\sum _j^{i}distance(a_i,a_j)\text{\hspace{1em}(2)}$$
$$distance(a_i,a_j)=virtualCateDistance(a_i,a_j)\ast spanWeight(|i-j|)\text{\hspace{1em}(3)}$$
虚拟类目相似度与item间距综合考虑.

Eq(2) is a special case of the NP-hard (Non-deterministic Polynomial time problem) maximum set cover problem.
We have to use an iterative greedy procedure to obtain a near-optimal solution.

(5) A i + 1 = A i ∪ { arg ⁡ max ⁡ a ∈ A − A i ρ ( A i ∪ { a } ) } A_{i+1}=A_i \cup \{\underset{a\in A-A_i}{\arg\max} \rho(A_i\cup \{a\})\} \tag 5 Ai+1​=Ai​∪{a∈A−Ai​argmax​ρ(Ai​∪{a})}(5)

simple wide used solution

分享一种很简单, 应用也很广泛的做法.
定义两个元素之间的相似度 d i s t a n c e ( i , j ) ∈ { 0 , 1 } distance(i,j) \in \{0,1\} distance(i,j)∈{0,1}, 电商推荐中可以认为两个商品同类目,同店铺, 同品牌 等, 命中其一就是相似.
$$distance(a_i,a_j)=\{\begin{array}{ll}0& ,a_i与a_j类目相等,作者相等...\\ 1& ,others\end{array}$$
定义元素和集合之间的相似度
$distance(S,a)=\sum _{b\in S}distance(a,b)$
那么迭代过程就是:
(10) A i + 1 = A i ∪ { arg ⁡ max ⁡ a ∈ A − A i , d i s t a n c e ( A i , a ) = 0 s ( a ) } A_{i+1}=A_i \cup \{ \underset{a\in A-A_i, distance(A_i,a)=0} {\arg\max} s(a) \} \tag {10} Ai+1​=Ai​∪{a∈A−Ai​,distance(Ai​,a)=0argmax​s(a)}(10)

即在所有满足打散的结果中选取最相关的那个.

mmr&rule mix rerank

伪代码.

参考

1. Adaptive, Personalized Diversity for Visual Discovery
2. min-presentation, MMR