题目1: 阿里2022.0407场算法在线笔试, 单选第4题
问: 牛牛群里聊天的时候,总会有人说“停停”("ting ting"),但是有的人却想表达的意思是"搞快点"("gkd")。也就是说如果一个人说 "ting ting" 他可能表达的意思有两种:"ting ting" 和 "gkd", 同理连续三个“ting”组成的 "ting ting ting" 则有三种含义:"ting gkd", "ting ting ting", "gkd ting"。四个"ting以此类推。若4l6 个"ting" 相连有 x 种含义,则 x mod 10 的值为多少?
解法一: 可用斐波那契数列的递推规律去解. f(n) = f(n-1)+f(n-2), 解释为 n 个 "ting"(以下简称单词) 的不同含义数,等于 固定第一个单词,后续 n-1 个单词的含义数 + 合并前两个单词为 "gkd",后续 n-2 个单词的含义数。由于无法手动算,需借助编程,递归去解。此时复杂度依旧很高,可引入记忆数组,此时秒解。还需注意数值溢出,考虑到题目要求,计算过程中也可只保留个位数。py代码见下。
ans = [0] * 500
def f(n: int) -> int:
if n <= 3:
return n
if ans[n] == 0:
ans[n] = f(n - 1) + f(n - 2)
# 数值太大防止溢出
ans[n] = ans[n] % 10
return ans[n]
print(f(416))
解法二: 用排列组合的思路去解。, 解释为有0个 "gkd",1个"gkd",2个"gkd" ,等等,以此类推的结果的加和。这个有没有个位数的什么规律,手动能不能求解,还不确定, 但代码一定可以秒解,见下.
def f2(n: int) -> int:
from scipy.special import comb, perm
ans = 0
for i in range(0, n):
if i <= n - i:
ans += comb(n - i, i, exact=True)
ans = ans%10
return ans
题目2: 对以往数据分析结果表明,当机器调整得良好时,产品的合格率为98%,而机器发生某一故障时,产品的合格率为55%,每天早上机器开动时,机器调整达良好的概率为95%。试求已知某日早上第一件产品是合格品时,机器调整达良好的概率是多少?
答:设事件A:产品合格;B:机器调整良好。已知P(A|B)=0.98,P(A|B的逆)0.55,P(B)=0.95。
求P(B|A)。
P(B|A)=P(AB)/P(A)=P(A|B)P(B)/[P(A|B)P(B)+P(A|B的逆)P(B的逆)]=0.97。
此题为贝叶斯公式的应用。
题目3: 阿里2022.0407场算法在线笔试, 单选第1题
问: 已知进入某商场的男性和女性中,45%的女性和15%的男性会进行消费,随机挑选一人,这个人进行了消费,则这个人是男性的概率是__? 假设进入该商场的男性和女性比例为 1:4.
答: P(Male | buy)
= P(M*buy) / P(buy)
= p(M)p(buy|M)/p(buy)
= 0.2*0.15/(0.8*.45+0.2*0.15)
= 0.0769
题目4: 将15名新生随机地平均分配到三个班级中去,其中有3名优等生。问:
(1)每班各分配到一名优等生的概率;
(2)这三人被分配到同一班中的概率。

题目5:阿里2014春,实习生招聘笔试
问:现有三个包,甲包两个白球,乙包两个黑球,丙包一白一黑。现随机从一个包中随机挑一个球,为白色。问再从此包中拿一个球仍为白色的概率是多少?
答:
再从此包中拿一个球仍为白色,意味着所选的包是甲包。
事件A:所挑的包为甲包;
事件B:随机从一个包中随机挑一个球,为白色。
P(A)=1/3,P(B)=(1/3)*1+(1/3)*(1/2)=1/2;
所求为P(A|B)=P(AB)/P(B)=P(B|A)*P(A)/P(B)=1*(1/3)/(1/2)=0.66。
此题考查条件概率,贝叶斯公式。
题目6: n个不同元素顺序入栈,共有多少种不同的出栈序列?
答:设入栈动作为0,出栈动作为1。一个入栈动作必然对应这一个出栈动作,n个元素的入栈和出栈就是n个0和n个1的排列。
我们需要求出可行的入出栈排列。故该问题可划归为:
n个0和n个1的排列,在任意位置之前,0的个数不少于1的个数。
卡塔兰数公式
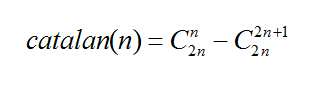





















 444
444

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








