堆排序详解与Java实现-优快云博客

前言

堆排序很重要的排序算法，它的时间复杂度是O(NlgN)。堆排序虽然没有快速排序常用，但是他提供的数据结构很优秀，比如优先队列的就是基于堆这个数据结构实现的。

堆数据结构简介

堆就是一个完整的二进制树，树中的每一个节点对应着数组中的元素。

如图所示

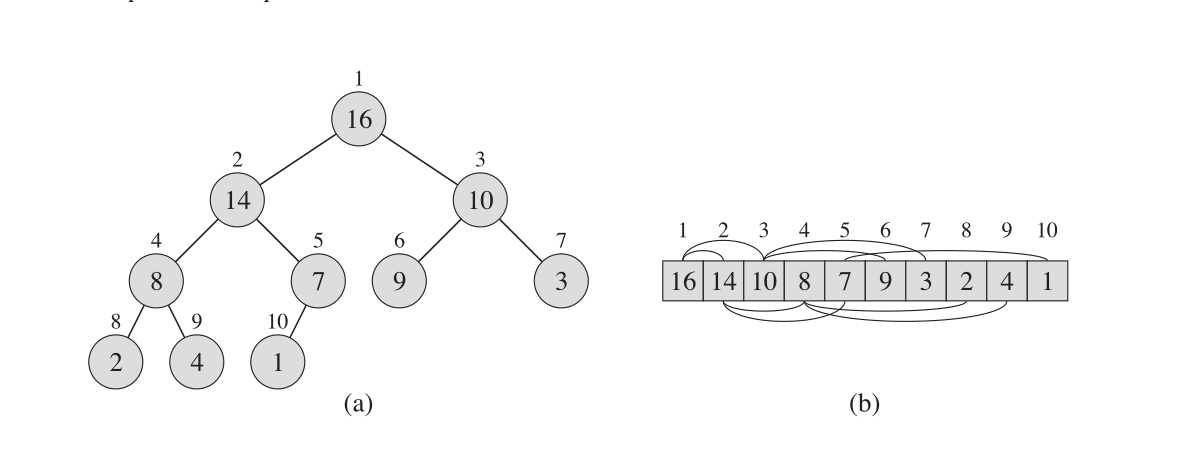
给定一个节点的索引 i，那么计算这个节点的父节点，左节点，右节点的公式是：

Parent(i)
 return i/2
Left(i)
 return i*2
Right(i)
 return i*2+1

需要注意的是，计算父节点的结果需要去掉小数点。举例 3/2=1.5，实际父节点的索引是1。

计算上述公式是非常快的（大多数计算机都是原生支持移位操作）：计算i/2时，只需要将操作数i向右移动一位，消耗一个指令，计算i*2时，只需要将操作数向左移动移位，消耗一个指令。

堆分两种，最大堆和最小堆，最大堆必须满足：A[parent(i)]>=A[i]。

到此堆的定义就结束了。开始介绍堆排序

堆排序的关键步骤有三个：保持最大堆，构建最大堆，堆排序算法。

保持最大堆

为了保持最大堆属性，我们调用MAX-HEAPIFY方法。这个方法的输入是数组A和数组A中的一个索引i。当调用这个方法的时候，它默认根在LEFT(i)和RIGHT(i)的二进制树是最大堆，但是A[i]这个节点可能比它的子树要小。MAX-HEAPIFY方法让A[i]这个元素下沉，从而使以索引i为根的二进制树保持最大堆的属性。

贴上算法导论里的伪代码

这个算法的实现使用了递归，所以很简洁易懂：首先计算左右子树的索引位置，当索引位置合法的情况下，和A[i]比较大小，并将最大值的索引位置记录下来，最后判断存储最大值索引位置是不是位置i，如果是，那就保持了最大堆属性，程序结束，如果不是，那就将这两个索引位置的值交换，递归的调用MAX-HEAPIFY(A,largest)。解决问题。

组建一个最大堆

我们使用从底至上的顺序调用MAX-HEAPIFY方法来组建一个最大堆。注意，叶子节点本身就是最大堆，所以这个方法的开始节点是A.length/2去掉小数点，结束节点是第一个节点。

贴出伪代码：

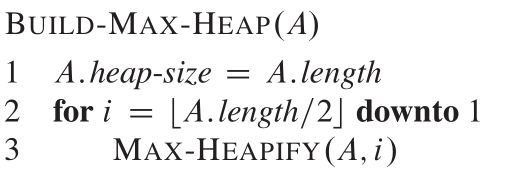
堆排序

堆排序开始使用组建最大堆方法的组建一个堆：A[1...N]，堆大小n=A.length。由于最大的元素已经在A[i]，我们通过交换A[1]和A[N]的方式将最大的元素放在最后位置。如果我们抛弃节点n，我们观察这个新的二进制树：新增的节点A[1]很可能会破坏最大堆的性质。没关系，我们可以调用构建最大堆方法MAX-HEAPIFY(A,1)，此时堆A=[1...n-1]。堆排序算法重复这样的步骤，直到堆的大小是2。

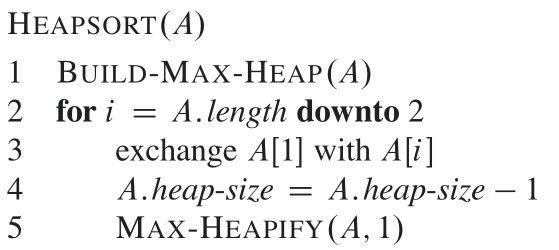
后记

算法的确是我的硬伤，但这也是计算机技术的基础，既然反抗不来，那就勉强享受这样的过程把，哈哈哈！

贴上java的简单实现:

package test;

public class HeapSortDemo1 {

	  public static void main(String[] args) {
	    //初始化数组
	    int arr[] = {9, 4, 8, 3, 1, 2, 5};
	    System.out.print("Initial Array  : ");
	    printArray(arr);
	    arr = heapsort(arr);
	    System.out.print("After Sorting  : ") ;
	    printArray(arr);
	  }
	  public static void printArray(int[] arr) {
	    for(int i = 0; i < arr.length; i++) {
	      System.out.print(arr[i] + " ");
	    }

	    System.out.println();
	  }
	  //以非递减顺序排列数组
	  public static int[] heapsort(int arr[]) {
	    int N = arr.length;
	    //创建一个堆
	    MaxHeap heap = createHeap(arr, N);

	    //重复以下步骤，直到堆的大小为1
	    while(heap.len > 1) {
	      //在堆中把最大值和最后一个值交换
	      swap(heap, 0, heap.len - 1);
	      heap.len--;//堆的大小减1
	      heapify(heap, 0);
	    }

	    return heap.arr;
	  }
	  public static MaxHeap createHeap(int arr[], int N) {
	    MaxHeap maxheap = new MaxHeap(N, arr);
	    int i = (maxheap.len - 2) / 2;

	    while(i >= 0) {
	      maxheap = heapify(maxheap, i);
	      i--;
	    }

	    return maxheap;
	  }
	  public static MaxHeap heapify(MaxHeap maxheap, int N) {
	    int largest = N;
	    int left = (N<<1) + 1; //左边孩子的索引
	    int right =(N<<1) + 2; //右边孩子的索引

	    if(left < maxheap.len && maxheap.arr[left] > maxheap.arr[largest])    {
	      largest = left;
	    }

	    if(right < maxheap.len && maxheap.arr[right] > maxheap.arr[largest]) {
	      largest = right;
	    }

	    if(largest != N) {
	      swap(maxheap, largest, N);
	      heapify(maxheap, largest);
	    }

	    return maxheap;
	  }
	  public static void swap(MaxHeap maxheap, int i, int j) {
	    int temp;
	    temp = maxheap.arr[i];
	    maxheap.arr[i] = maxheap.arr[j];
	    maxheap.arr[j] = temp;
	  }
	  static class MaxHeap {
	    int len;
	    int arr[];
	    MaxHeap(int l, int a[]) {
	      len = l;
	      arr = a;
	    }
	  }
}

转载于:https://my.oschina.net/huaxiaoqiang/blog/3016846