关于数字签名、数字证书,之前只知道是和双秘钥加密RSA有关,而且加密方法也只是初步了解,现在整理下。
参考文章:
http://www.ruanyifeng.com/blog/2011/08/what_is_a_digital_signature.html(数字签名是什么?)
http://www.ruanyifeng.com/blog/2006/12/notes_on_cryptography.html(密码学笔记)
http://www.ruanyifeng.com/blog/2013/06/rsa_algorithm_part_one.html(RSA加密算法原理:数论知识)
http://www.ruanyifeng.com/blog/2013/07/rsa_algorithm_part_two.html(RSA加密算法原理:实现)
http://www.ruanyifeng.com/blog/2016/08/migrate-from-http-to-https.html(https升级指南)
(1)加密方法的分类
加密方法分为两类:单钥加密、双钥加密。
单钥加密:加密和解密过程都用同一套密码。又称“对称加密”或者“私钥加密”。
双钥加密:加密用一套密码,解密用另一套密钥。又称“非对称加密”或者“公钥加密”。
(2)单钥加密的典例:代换加密
代换加密就是一种典型的单钥加密,加密和解密都用同一套密钥,下图中明文与密文的转换规则也就是密钥:

假设明文为 syk,那么通过密钥加密后就可得到密文为 VBC,同样通过密文通过同一套密钥也可以得出明文。
除了代换加密外,还有很多单钥加密的例子,其中【DES加密】也是很经典的,这里就先不详述了。
(3)双钥加密
单钥加密,又称“私钥加密”、“对称加密”,它的缺点主要在于需要把密钥告知给解密方,这就存在密钥的传递,也就有丢失的风险,不安全。
双钥加密,又称“公钥加密”、“非对称加密”,它就很好的解决了单钥加密需要传递私钥的问题,可以说是计算机信息安全方面,最重要的一种加密方法了。
双钥加密,一把为公钥,一把为私钥,原理如下:
a) 公钥和私钥是一一对应的关系,有一把公钥就必然有一把与之对应的、独一无二的私钥,反之亦成立。
b) 所有的(公钥, 私钥)对都是不同的。
c) 用公钥可以解开私钥加密的信息,反之亦成立。
d) 同时生成公钥和私钥应该相对比较容易,但是从公钥推算出私钥,应该是很困难或者是不可能的。
(4)双钥加密的实现:RSA 加密算法
1977年,三位数学家Rivest、Shamir 和 Adleman 设计了一种算法,可以实现非对称加密(即双钥加密),也就是 RSA 加密算法。
RSA 加密算法非常可靠,密钥越长,它就越难破解,可以说有计算机网络的地方,就有 RSA 加密算法。
目前被破解的最长 RSA 密钥是 768 个二进制位。也就是说,长度超过 768 位的密钥,还无法破解(至少没人公开宣布)。因此可以认为,1024 位的RSA密钥基本安全,2048 位的密钥极其安全。
(5)RSA 加密算法所需的数论知识
一、质数:
一个数只能被 1 和本身整除,那么这个数就是质数。如 1 、3、 5、 7、 ....... 。
其中,能整除给定正整数的质数,称为质因数。
17世纪时,法国修道士梅森(Marin Mersenne)提出了一个质数计算公式:2^n - 1,称为梅森公式。符合该公式的质数,就称为梅森质数,如下图:

二、互质关系:
如果两个正整数除了1以外,没有其他公因子,则两者为互质关系。如 15 和 32 、 3 和 7

三、欧拉函数:
任意给定正整数n,请问在小于等于n的正整数之中,有多少个与n构成互质关系?求这个值的函数,就称为欧拉函数。
如在1到8之中,有多少个数与8构成互质关系?答:有1 , 3 , 5 , 7 这个四个数,所以为 4。计算公式如下:

四、欧拉定理:
若 n , a 为正整数,且 n , a 互质,则:
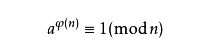
五、模反元素:
如果两个正整数a和n互质,那么一定可以找到整数b,使得 ab-1 被n整除,或者说ab被n除的余数是1。那么 b 就是 a 的模反元素:
b = a 的 φ(n)-1 次方
(6)RSA 加密算法的具体实现
公钥私钥的生成,以及使用它们去加密解密,这些步骤还是原文写得清楚,详细的我还是去看:
http://www.ruanyifeng.com/blog/2013/07/rsa_algorithm_part_two.html
(7)数字签名、数字证书
通过“双钥加密”(又称“公钥加密”、“非对称加密”),我们既能很好的实现内容的加密,又能够通过私钥,确定发送人。
假设小明有两把钥匙,一把为私钥,一把为公钥。
【数字签名】:
作用:小明用私钥对内容的摘要进行加密,生成“数字签名”,其他人通过小明的公钥进行解密,解密成功,则证明是对应的人(小明)发送的。
过程:小明要想其他人发送内容,使用私钥对摘要(也就是内容的一部分)加密,生成"数字签名",和内容一起发送。其他人接收到后,使用小明的公钥进行解密,如果能解开,则证明的确是小明发送的(这就是数字签名的作用),同时如果解密后的摘要的内容与实际的内容一致,则证明内容没有被人中途修改。
【数字证书】:
起因:在数字签名的使用过程中,其他人接受的数据,需要用小明的公钥进行解密,可是如何保证自己拿到的公钥是小明的呢?因为可能存在有人假冒小明,得到的公钥并不是小明的,导致一直误以为是小明发送的数据。为了解决公钥的所属问题,数字证书就出现了。
作用:为了保证其他人拿到的公钥是小明的,"证书中心"(certificate authority,简称CA),为公钥做认证,CA用自己的私钥对对应人的信息和公钥进行加密,生成“数字证书”。其他人用CA的公钥(无法假冒,CA的公钥存于其网站中,可下载)对“数字证书”解密,从而得到对应人的公钥,并证明公钥是属于对应人的。
过程:
a)小明在发送信息时,将“数字签名”、“数字证书”、内容一起发送
b)其他人接收到后,根据CA的公钥(这个假冒不了,因为这些公钥都是在对应的CA官网下载的)对“数字证书”进行解密,得到小明的信息和公钥,证明得到的公钥是小明的。
c)再使用小明的公钥对“数字签名”进行解密,证明是小明发送的。
d)对比数字签名中的摘要,以及发送的内容,证明内容在发送过程中未被修改。
注意:使用数字证书时,自己的“公钥“是证书机构提供的,而私钥是自己设定的,两者结合形成双钥加密。
(8)https协议中加密的使用
首先,客户端向服务器发出加密请求。从 http 升级为 https 可参考:http://www.ruanyifeng.com/blog/2016/08/migrate-from-http-to-https.html(https升级指南)
注意:公钥是证书机构提供的,私钥是自己设定的,两者结合形成双钥加密。
服务器用自己的私钥加密网页以后,连同本身的数字证书,一起发送给客户端。
客户端(浏览器)的"证书管理器",有"受信任的根证书颁发机构"列表。客户端会根据这张列表,查看解开数字证书的公钥是否在列表之内。
如果数字证书记载的网址,与你正在浏览的网址不一致,就说明这张证书可能被冒用,浏览器会发出警告。
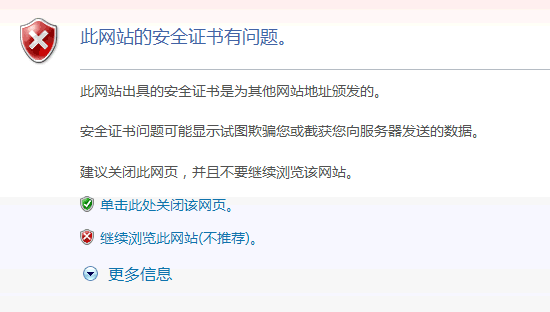
如果这张数字证书不是由受信任的机构颁发的,浏览器会发出另一种警告。
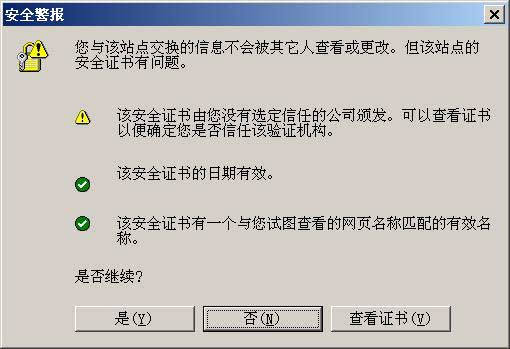
如果数字证书是可靠的,客户端就可以使用证书中的服务器公钥,对信息进行加密,然后与服务器交换加密信息。




 本文深入探讨了数字签名和数字证书的概念,解释了它们在确保数据安全和验证身份中的作用。通过双钥加密(公钥加密)机制,数字签名能够验证消息来源的真实性,而数字证书则确保了公钥的正确归属,防止了中间人攻击。文章还详细介绍了RSA加密算法的原理及其在生成公钥和私钥对中的应用。
本文深入探讨了数字签名和数字证书的概念,解释了它们在确保数据安全和验证身份中的作用。通过双钥加密(公钥加密)机制,数字签名能够验证消息来源的真实性,而数字证书则确保了公钥的正确归属,防止了中间人攻击。文章还详细介绍了RSA加密算法的原理及其在生成公钥和私钥对中的应用。

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








