支持向量机(SVM)
svm有三宝:间隔,对偶,核技巧。
svm又分成:hard margin svm;soft margin svm;kernel svm
间隔
svm思想:最大间隔分类器,
几何间隔:(点到直线的距离)
函数间隔:
对于所有的x,满足最近的x与分类平面最远。
即:max margin(w,b)
这是一个二次不等式凸优化。
hard margin svm
带约束优化目标:
拉格朗日去约束:
强对偶关系(线性二次凸优化问题满足强对偶):
后面的最小化拉格朗日函数可以先对b求导代入后再对w求导得到最优解w
最后优化函数变为:
===>
KKT条件<==>强对偶关系:
;
;
;偏导等于0
;约束
;
;
之前已得到:,通过KKT条件可得x不为支持向量时λ为0,所以
;(
)为支持向量。
(KKT条件只是为了得到b的最优解和得出最优解和对新样本的预测只和支持向量有关的结论???)
之前得到最后的优化函数只有λ一个变量,使用SMO算法可求得。
soft margin svm
思想:数据并不可分或存在噪声,允许一点点错误。
损失函数的构造:
①错误样本点的个数:
损失函数是不连续的,无法求解。
②使用错误点的距离表示:
损失函数:
令
求解过程和hard margin svm相同。
核方法背景介绍
kernel method:思想角度
kernel trick:计算角度
kernel function: (满足非线性转换的内积)。
1.非线性带来高维转换:对于严格的非线性,先进行给线性转换(模型角度)。
2.对偶表示带来内积,svm对偶表示后有样本内积的表示(优化角度)。
3.cover theorem:高维比低维更易线性可分。
正定核函数
核函数如果是正定核函数,则:
①对称性
②正定性:对应的gram matrix是半正定的。
或: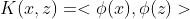 ;Φ属于希尔伯特空间。
;Φ属于希尔伯特空间。
希尔伯特空间:完备的(对极限是封闭的),可能是无限维的,被赋予内积(对称性,正定性,线性)的线性空间。





















 1103
1103

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








