STL序列式容器之heap（堆）

原创已于 2024-11-16 20:59:46 修改 · 775 阅读

19 ·

CC 4.0 BY-SA版权

文章标签：

#c++ #开发语言

于 2024-11-16 19:47:26 首次发布

STL学习专栏收录该内容

34 篇文章

订阅专栏

heap概述

heap并不归属于STL容器组件，它是幕后英雄，扮演了priority queue的助手；

priority queue允许用户以任意顺序将元素推入容器内，但是取出时，是按优先级最高的元素开始取。针对priority queue要求的特性，最直观的做法，有两种：

1:插入后，保持底层queue的排序状态，此时插入的时间复杂度是O(n);取数据可在常数时间内将元素取出

2:插入还是放在容器的末尾，插入的时间复杂度尾O(1);取数据时，需要遍历数组，而后取出最大的那个元素；时间复杂度为O(n);

此外为了能够获取O(logN)时间复杂度性能的插入和获取性能，可能会想到用二分查找树的方式（红黑树）；事实上如果采用红黑树的做法，也能实现该功能，只是再实现复杂度和存储容量上都会有一定程度上的提升；本文采用了binary heap的方式进行实现；

所谓binary heap就是一种complete binary tree（完全二叉树），也就是整颗binary tree除了最底层的叶子节点之外，是填满的，且最底层的叶子节点由左至右不得存在空隙。如下图所示

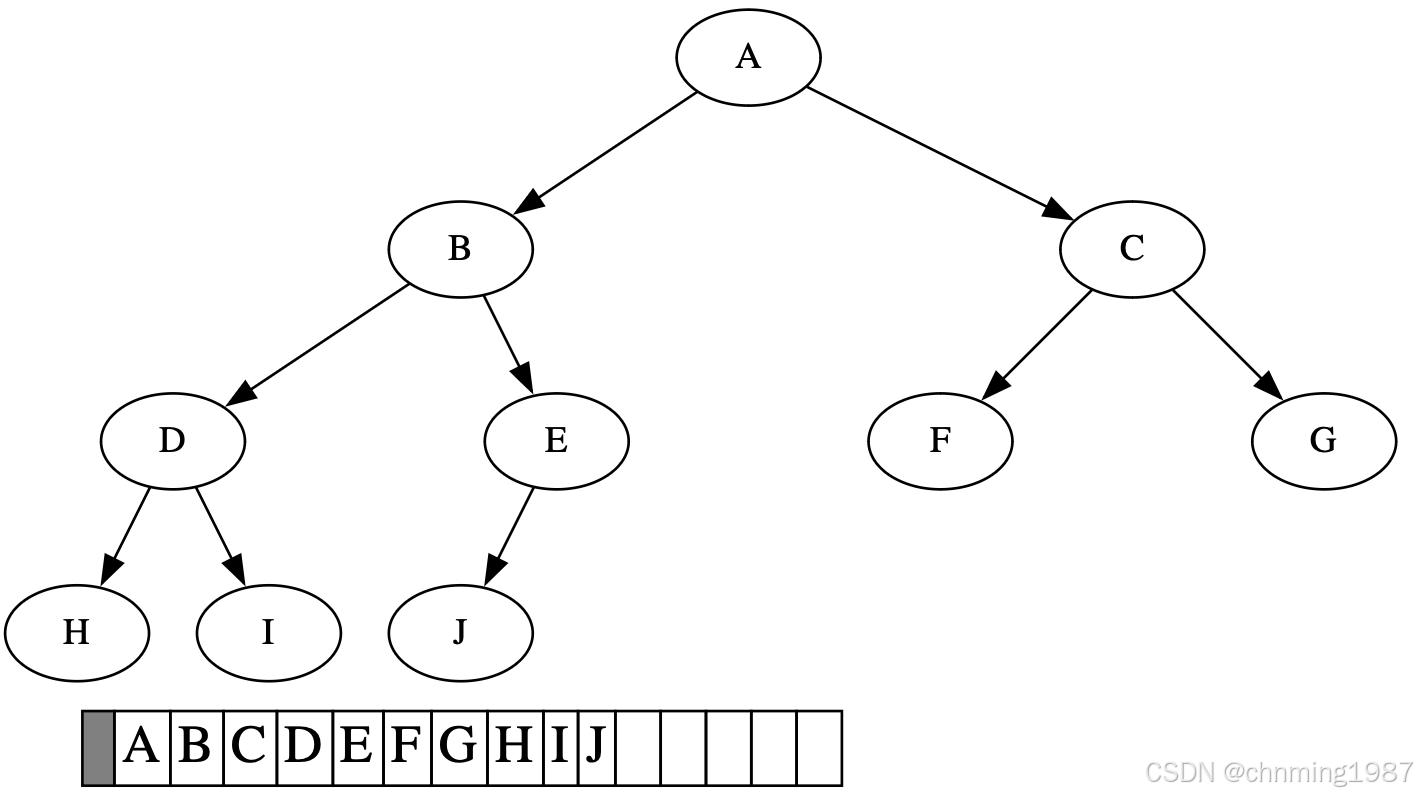
因为完全二叉树节点紧凑的特性；我们可以采用array来存储所有节点；其中i标识父节点的索引，则其左右子几点的索引分别为2*i 及2*i+1；如此一颗完全二叉树可以通过array进行表示，同时我们称这种表示法为隐式表述法（implicit representation）。

如此分析之后，我们需要的工具，可以采用一个array和一组heap算法（用于插入元素、删除元素、取极值，将某一整组数据排列成一个heap）。array的缺点是无法动态改变大小，而heap却需要这项功能，因此，以vector代替array。

根据元素排列方式，heap可分为max-heap和min-heap两种，前者每个节点的键值(key)都大于或等于其子节点键值，后者的每个节点键值(key)都小于或等于其子节点键值。因此，max-heap的最大值在根节点，并总是位于底层array或vector的起始处（front）；min-heap

的最小值在根节点，亦总是位于底层array或vector的起始处（front）。STL提供的max-heap，以下描述的算法都是指max-heap。

heap 算法

push_heap算法

push_heap,将元素加入heap中

heap初始状态如下：

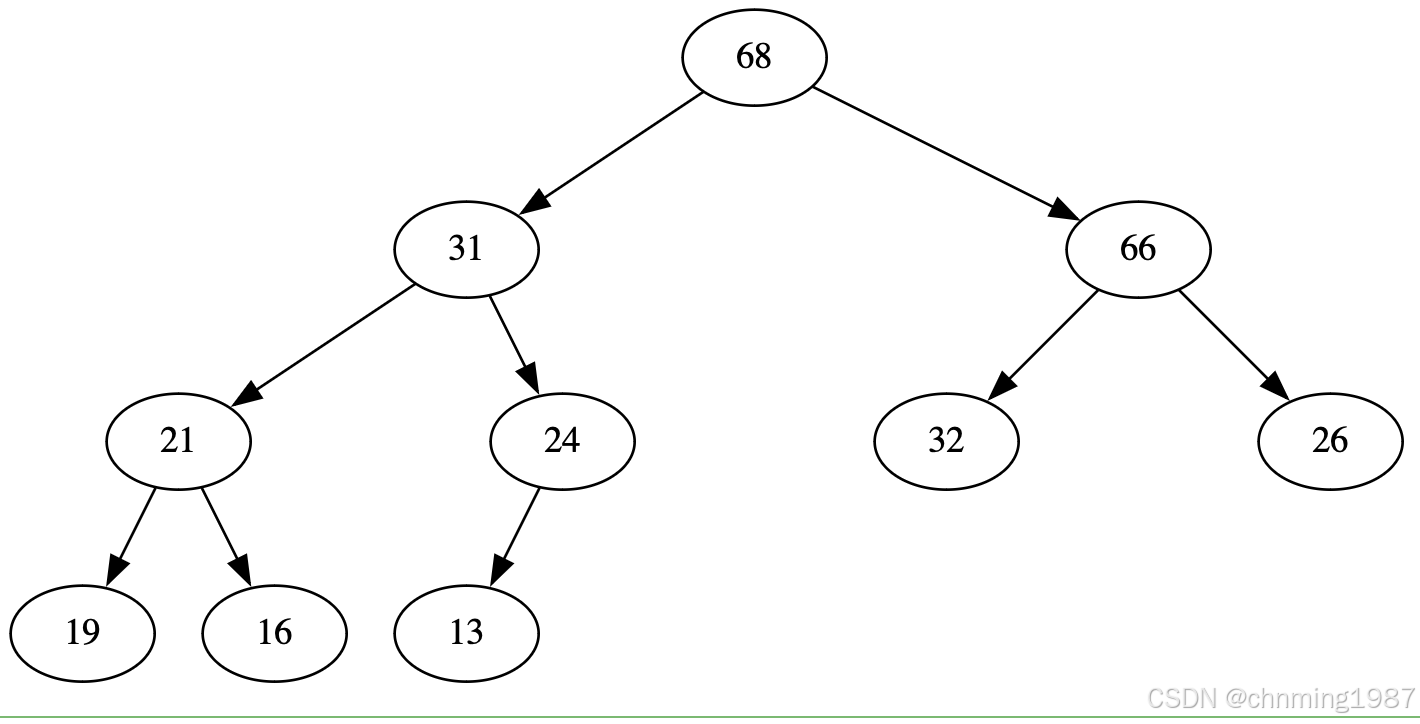
此时需要将新的节点加入heap中，假设加入新的节点的key为50.

此时待加入的节点位于heap的末尾，亦即tree最底层叶子节点的最右端

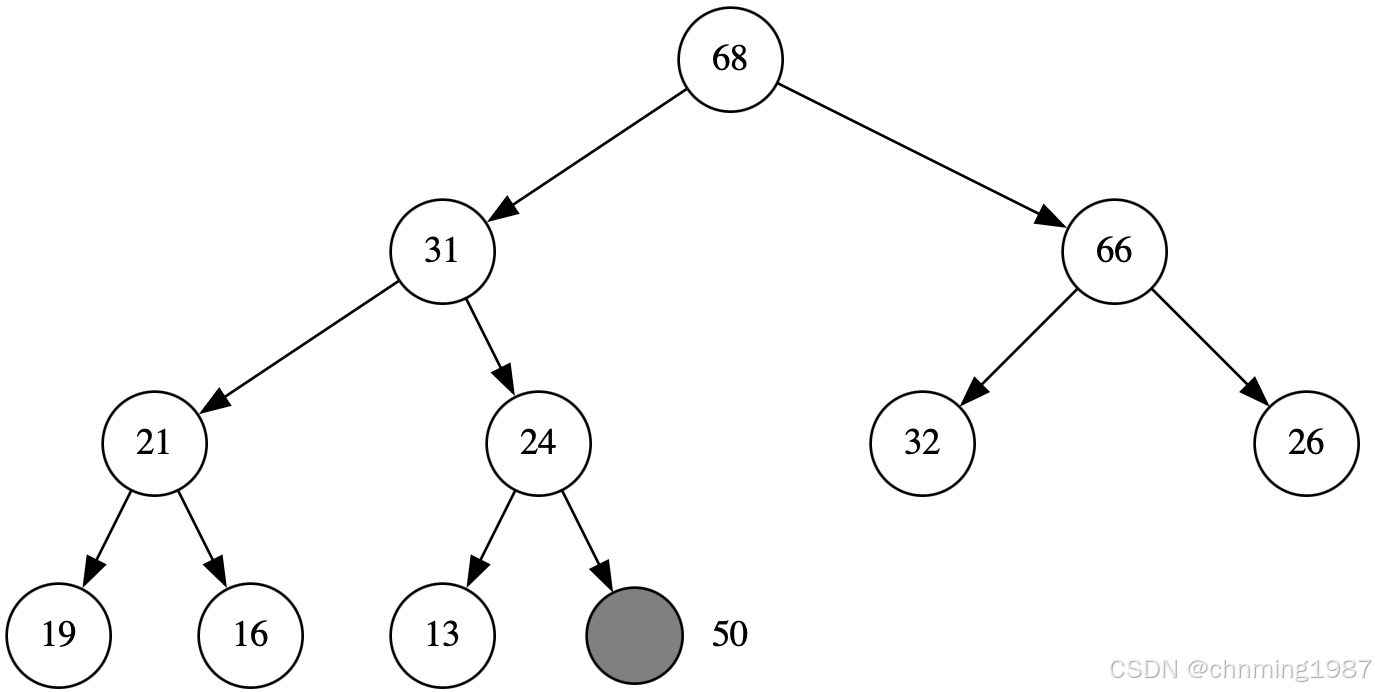
加入节点后，这颗树已不再满足max-heap的特性；通过percolate up（上溯）程序：将新节点拿来与其父节点比较，如果其键值(key)比父节点大，就父子节点进行交换(实际实现算法只是把父节点进行了下移)，如此一直上溯，直到不需要交换或直到根节点为止。执行过程如下：

1：当前节点key50比父节点key24来得大，所以交换当前父子节点；

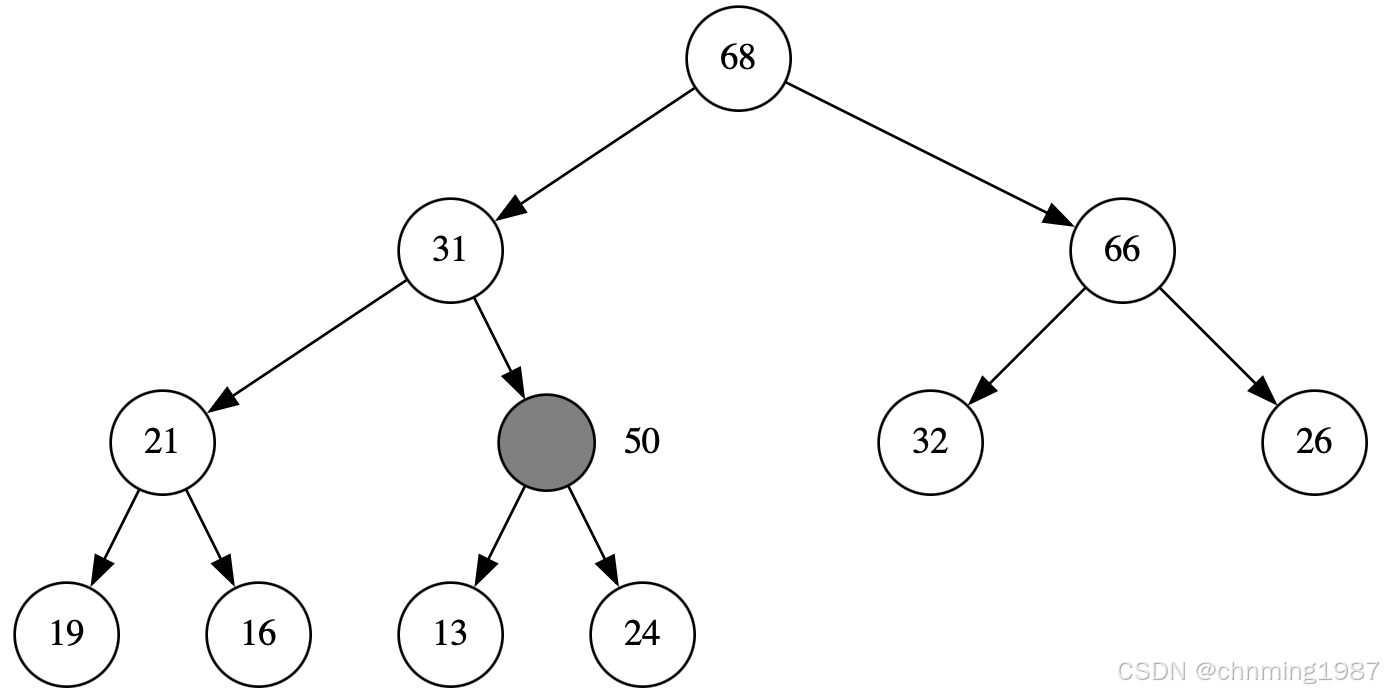
交换完成后，当前节点为值依然为50，但是其索引已经发生了改变，为原节点父节点的索引。而后继续进行上溯，上溯完后为：

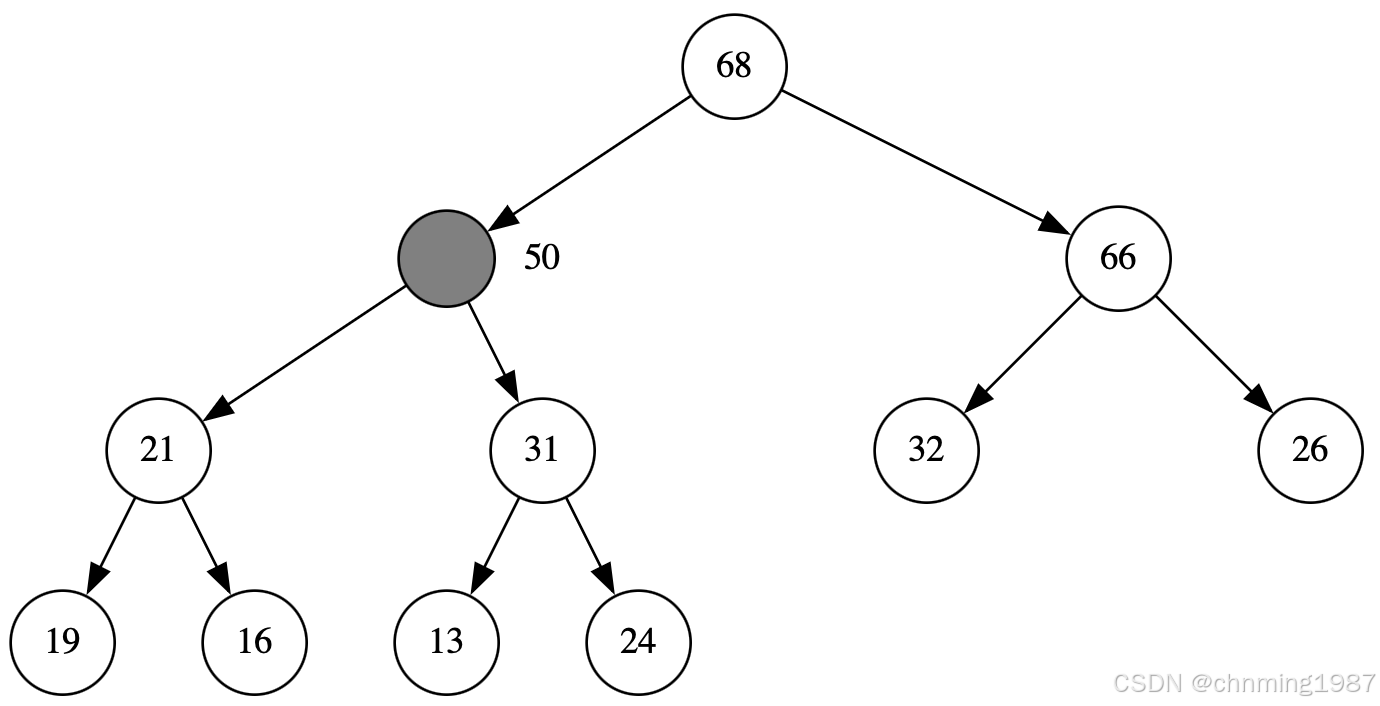
此时因为31比50来得小，所有有执行了一次上溯；而后继续进行上溯，发现父节点的key为68，大于当前节点的key50，所以上溯结束；将50填入当前节点；最终max-heap形如：

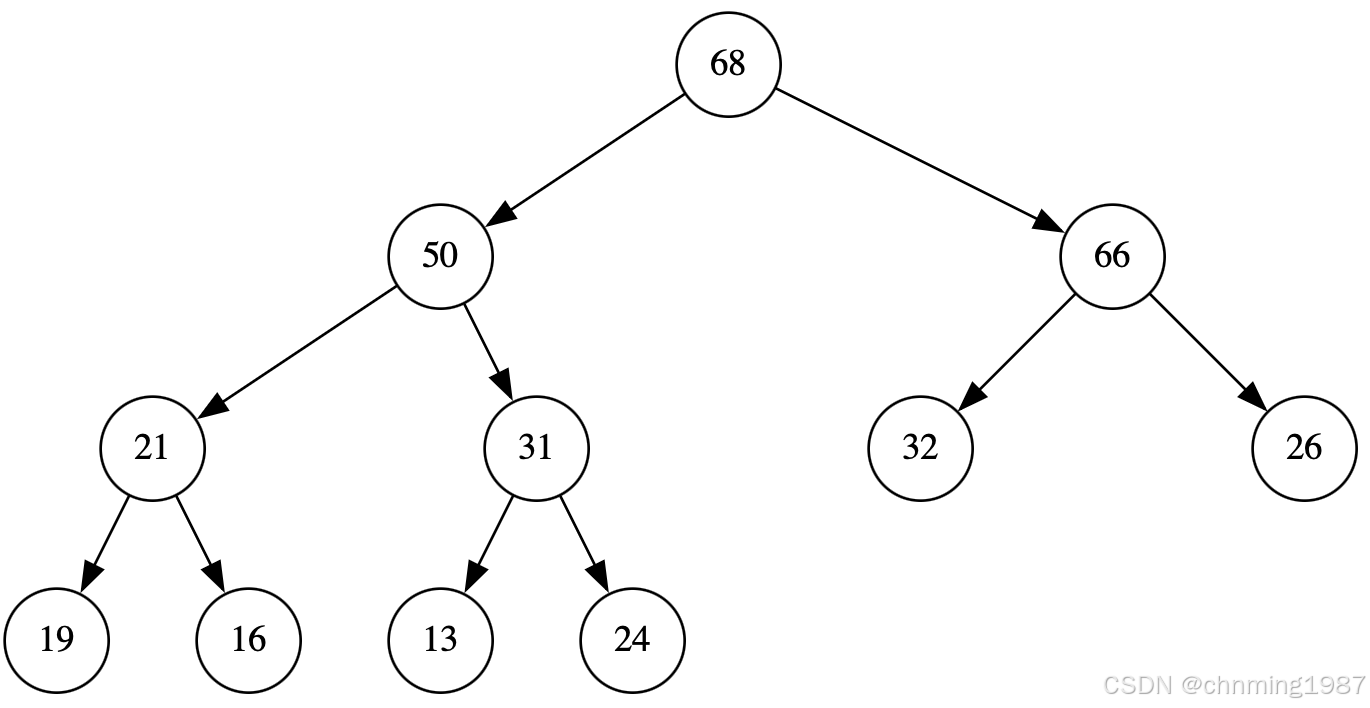
下面便是push_heap算法的实现细节。该函数接受两个迭代器，又来表现一个heap底部容器（vector）的头和尾，并且新元素已经插入到底部容器的最尾端（end()-1）。其代码如下：

template<class RandomAccessIterator>
inline void push_head(RandomAccessIterator first, RandomAccessIterator last) {
    __push_head_aux(first, last, distance_type(first), value_type(first));
}

template<class RandomAccessIterator, class Distance, class T>
inline void __push_head_aux(RandomAccessIterator first, RandomAccessIterator last, Distance*, T*) {
    __push_heap(first, Distance((last-first) - 1), Distance(0), T(*(last-1));
}


template <class RandomAccessIterator, class Distance, class T>
void __push_heap(RandomAccessIterator first, Distance holeIndex, Distance topIndex, T value) {
    Distance parent = (holeIndex -1) / 2;
    while (holeIndex > topIndex && *(first + parent) < value) {
        *(first + holeIndex) = *(first + parent);
        holeIndex = parent;
    }
    *(first+holeIndex) = value;
}

从实现算法的代码可以看出，前文提到的交换，实际上未进行真正的交换，而只是进行了父节点的下移，需要上溯的节点始终保存的value中，只是最后一步再进行了赋值操作；（这么做的好处是，可以减少一次每次“交换”的赋值操作，因为逻辑上的效果和交换是一样的）。

pop_heap算法

有对堆的插入操作，需要有配套的从堆中，pop优先级最高的元素的操作；操作函数名为pop_heap;既然是max-heap那么最大元素必然在根节点。pop取走根节点后，剩余元素将不在满足heap的特性，所以需要一系列操作进行修正；其修正过程如下：

1：将起始节点和尾部节点进行交换（交换完之后，尾部节点即为需要pop的节点，算法执行完后，可以调用vector的back()函数返回最大的key）

2：对于替换过来的尾部节点从top沿着tree往下进行下溯（percolate down）：将空间节点和其较大子节点进行“对调”（将子节点中的较大者放入当前空间，然后指针朝刚刚被调换的子树方向移动），直到叶子节点为止，将之前的尾部节点填入“空洞节点”；而后再执行一遍上溯（percolate up）程序；即完成了pop_heap操作；实例如下：

初始状态为

此时将，68节点放入最后节点，起始节点变成了空洞节点；而后24成为了待插入节点

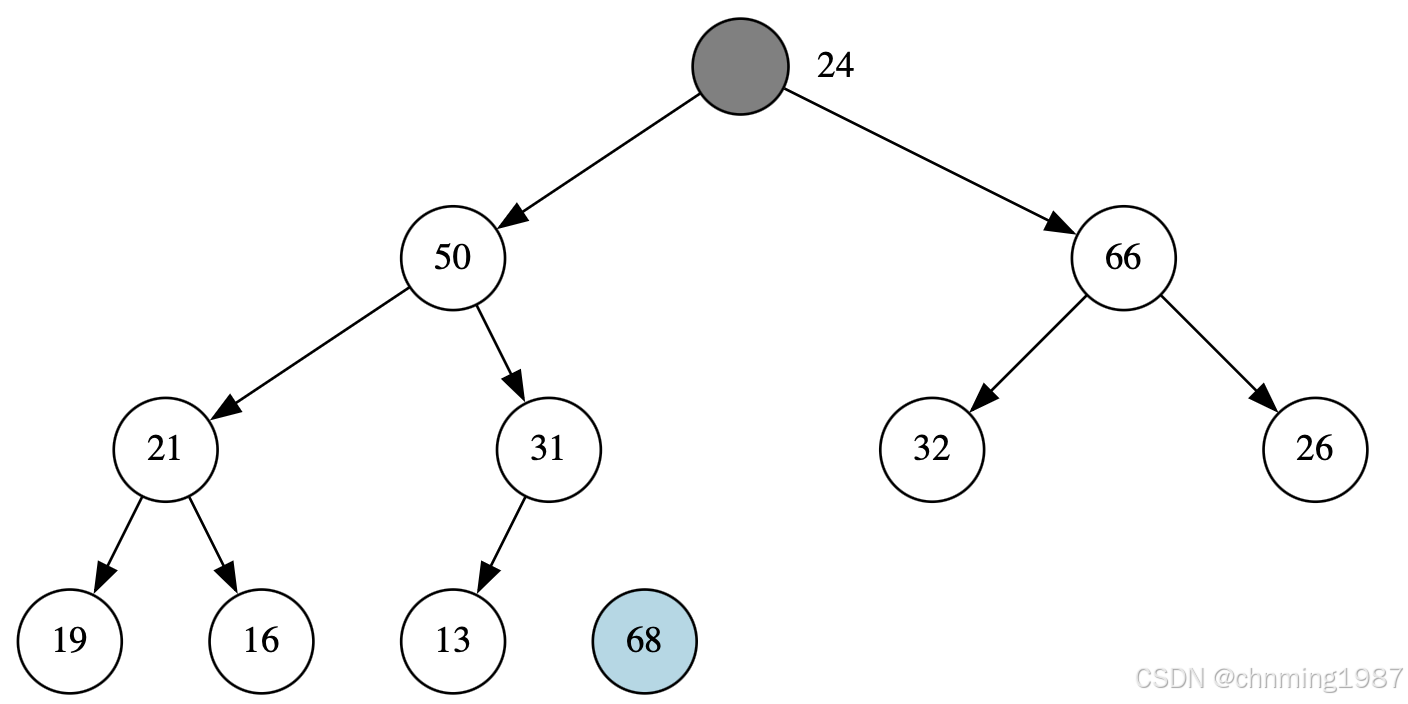
此时的holeIndex为0，而后判断两个子节点分别为66和50，取66进行交换：

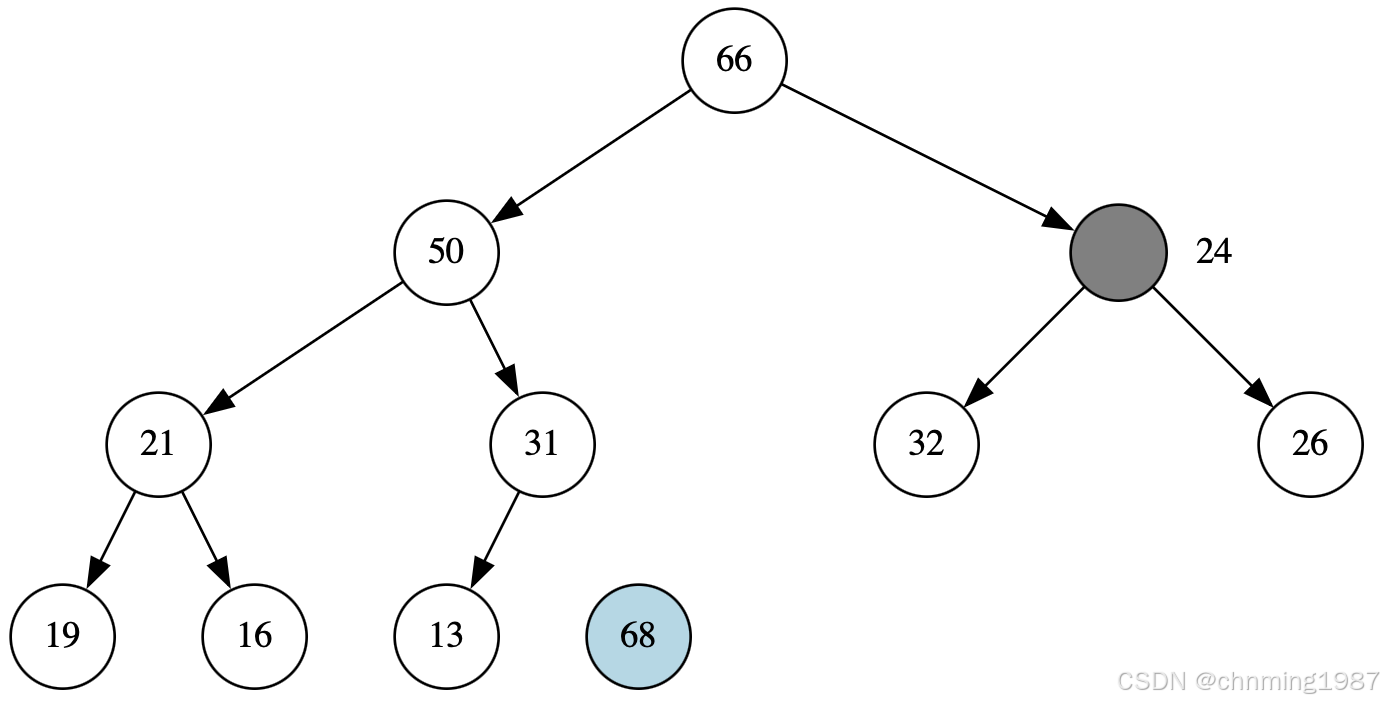
继续选择32作为交换节点：

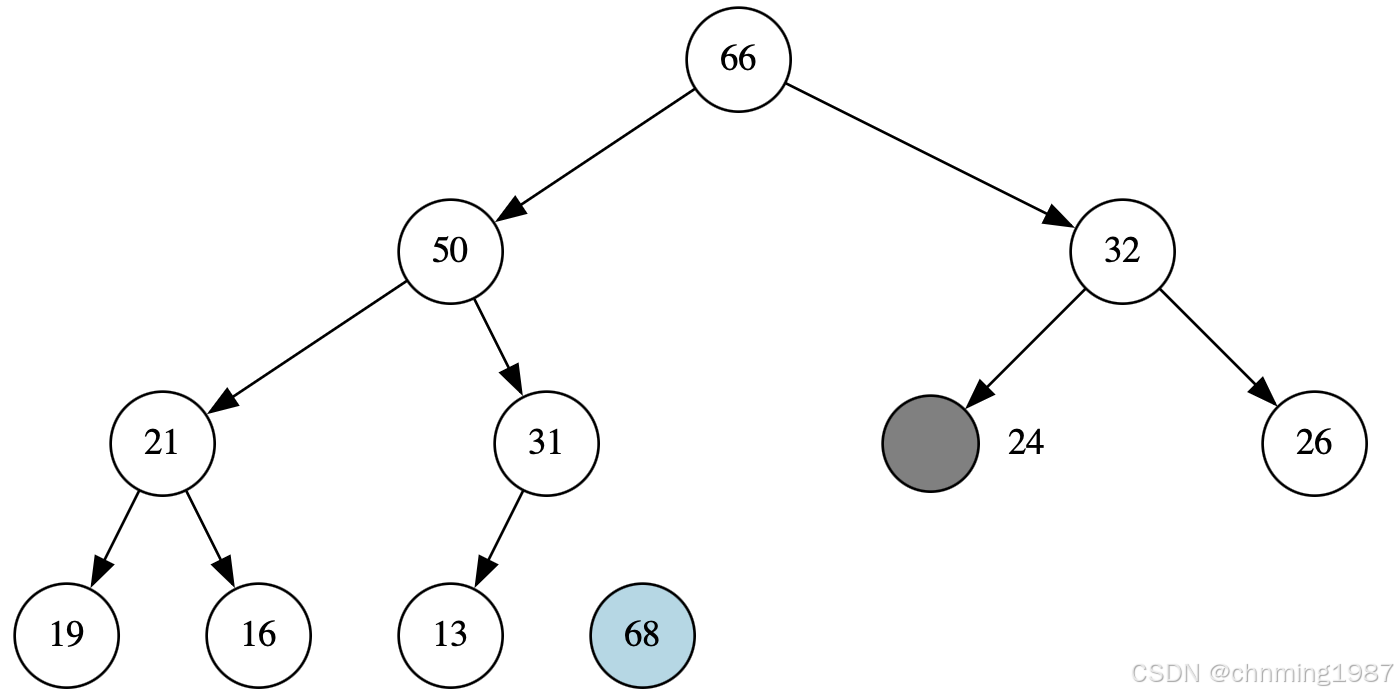
执行完以上步骤后，已经到达了叶子节点，然后针对24节点进行上溯操作；

因为24比32来得小，所以上溯执行到第一步就结束了。结果如下

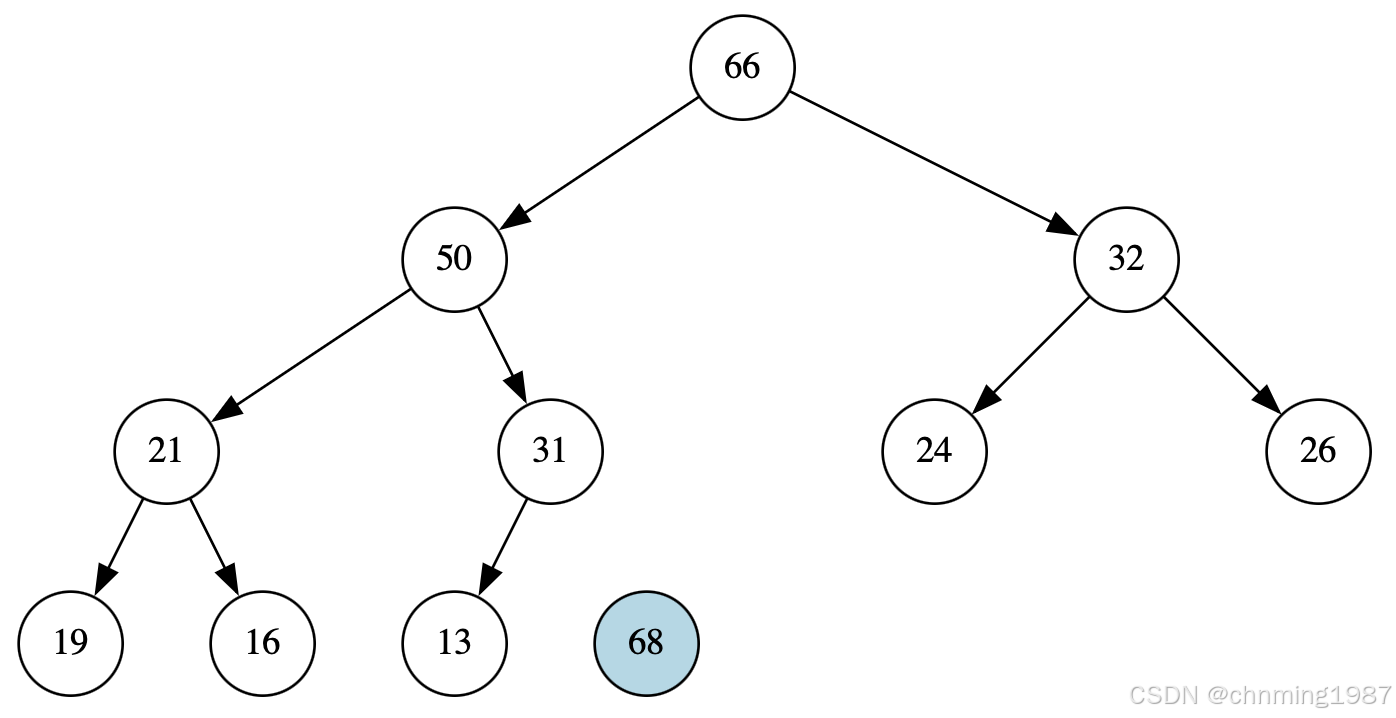
此时68节点存放在底层容器的最尾端，可通过c.back()获取key值最大的元素；同时剩余节点满足heap的特性；其代码如下：

template<class RandomAccessIterator>
inline void pop_heap(RandomAccessIterator first, RandomAccessIterator last) {
    __pop_heap_aux(first, last, value_type(first));
}

template<class RandomAccessIterator, class T>
inline void __pop_heap_aux(RandomAccessIterator first, RandomAccessIterator last, T*) {
    __pop_heap(first, last-1, last-1, T(*(last-1)), distance_type(first));
}

template<class RandomAccessIterator, class Distance, class T>
inline void __pop_heap(RandomAccessIterator first, RandomAccessIterator last, RandomAccessIterator result, T value, Distance*) {
    *result = *first;
    __adjust_heap(first, Distance(0), Distance(last-first), value);
}


template<class RandomAccessIterator, class Distance, class T>
void __adjust_heap(RandomAccessIterator first, Distance holeIndex, Distance len, T value) {
    Distance topIndex = holeIndex;
    Distance secondChild = 2*holeIndex + 2;
    while (secondChild < len) {
        if (*(first + secondChild) < *(first+secondChild - 1)) 
            secondChild --;
    
        *(first + holdIndex) = *(first + secondIndex);
        holdIndex = secondIndex;
        secondChild = 2*holeIndex + 2
    }
    
    if (secondChild == len) {
        *(first + holdIndex) = *(first + secondIndex - 1);
        holdIndex = secondIndex - 1;
    }

    __push_heap(first, holeIndex, topIndex, value);

}

sort_heap算法

基于之前pop_heap算法每次都能获取容器当中的最大元素；如果持续对heap进行pop_heap操作，每次将操作范围向前缩减一个元素，当整个程序执行完毕后，我们即可得到一个递增序列；操作过程如下所示：（为了便于展示，在节点的左侧加上了节点的索引相对first的距离）

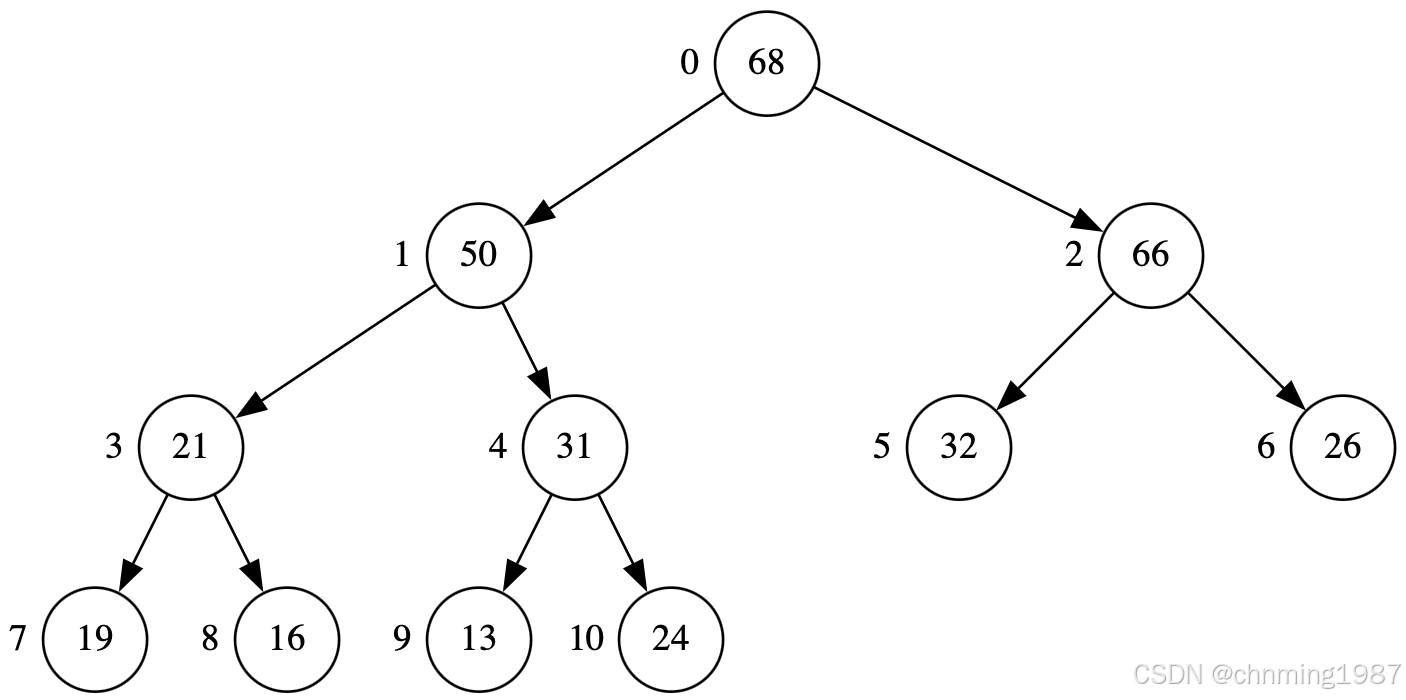
首先获取68，并调整heap后得到如下结构

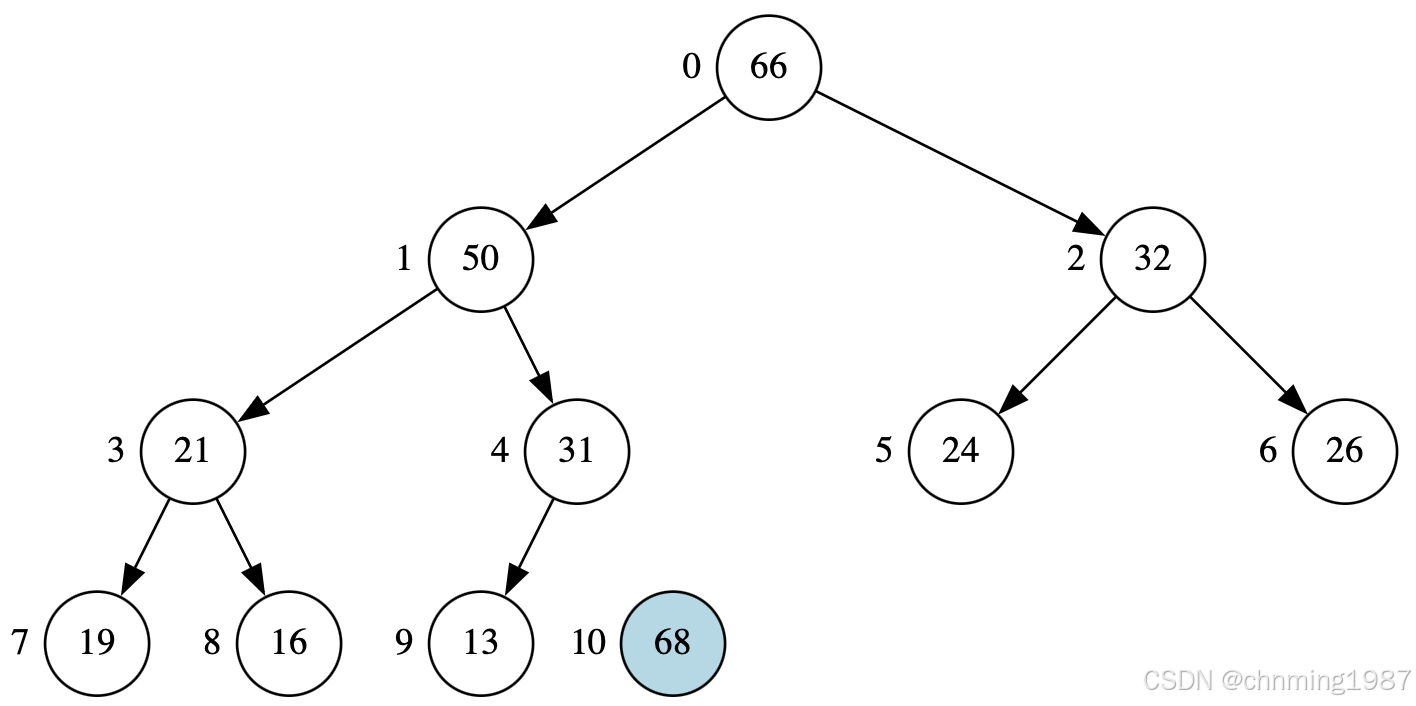
继续获取66，并调整堆

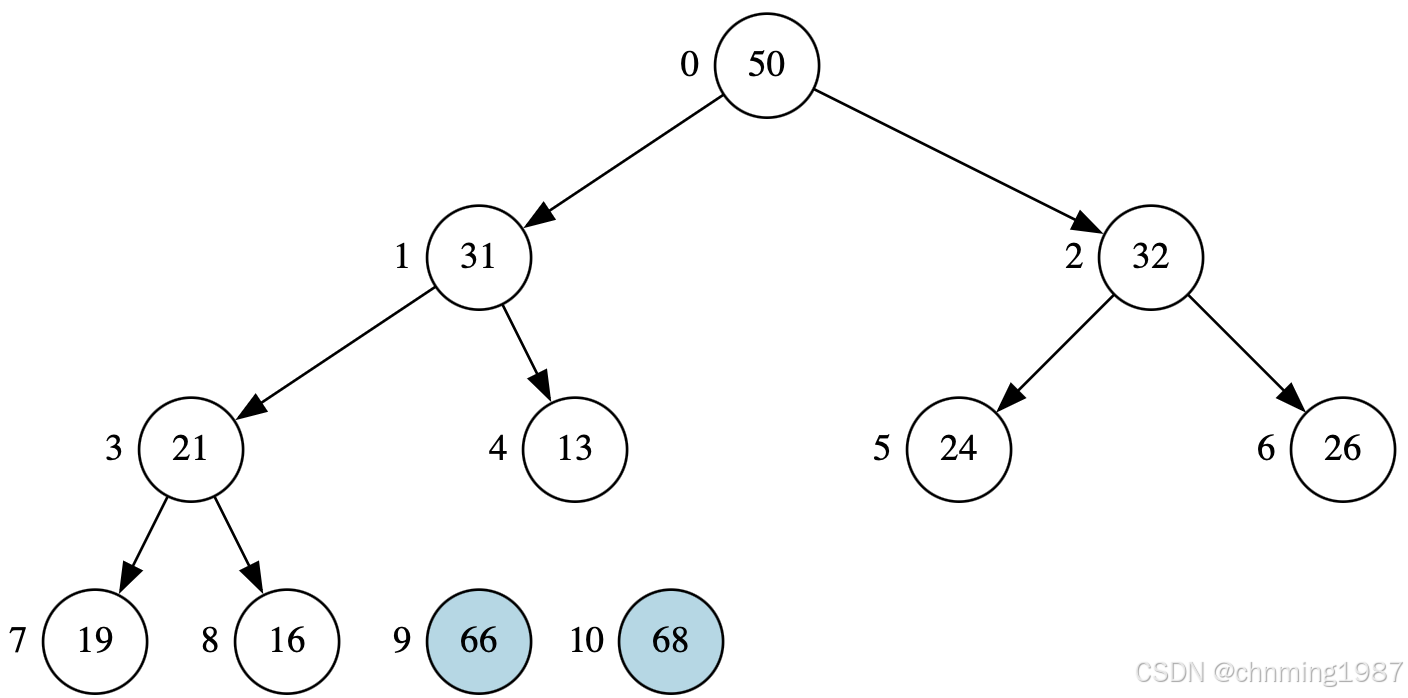
而后获取50，并调整堆

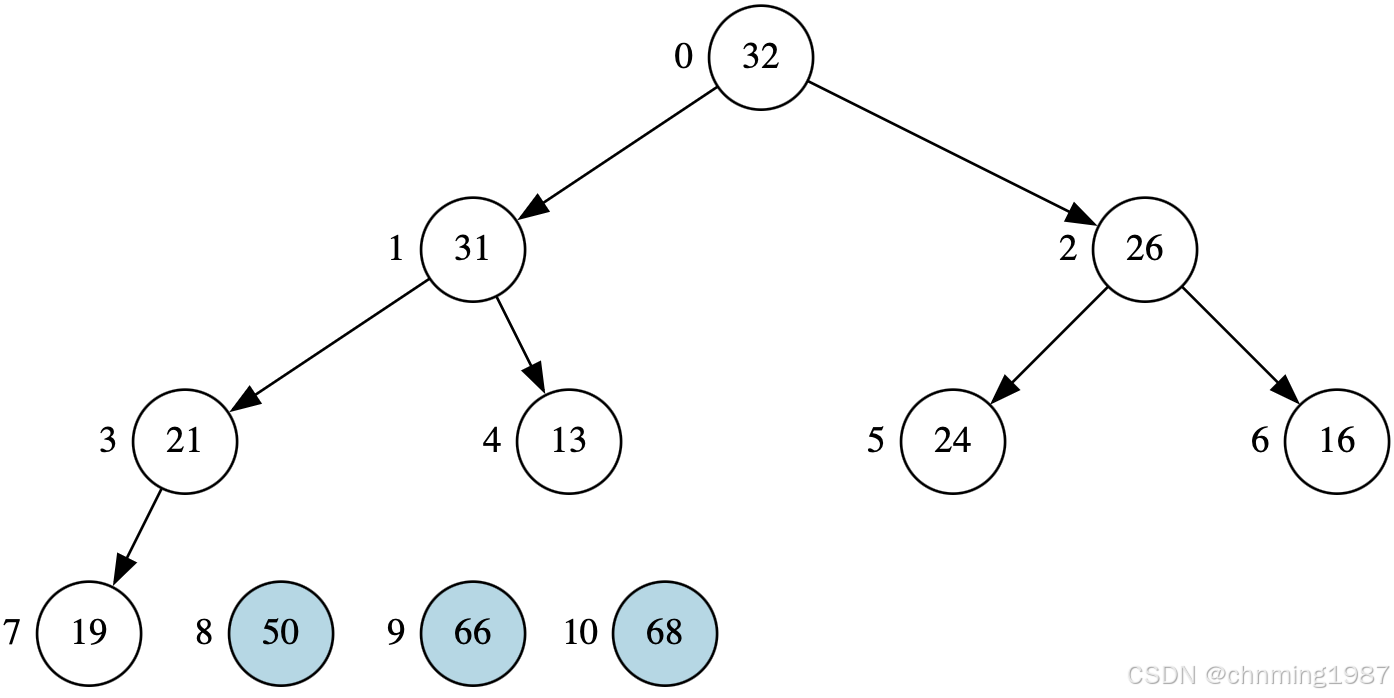
获取32，并调整堆

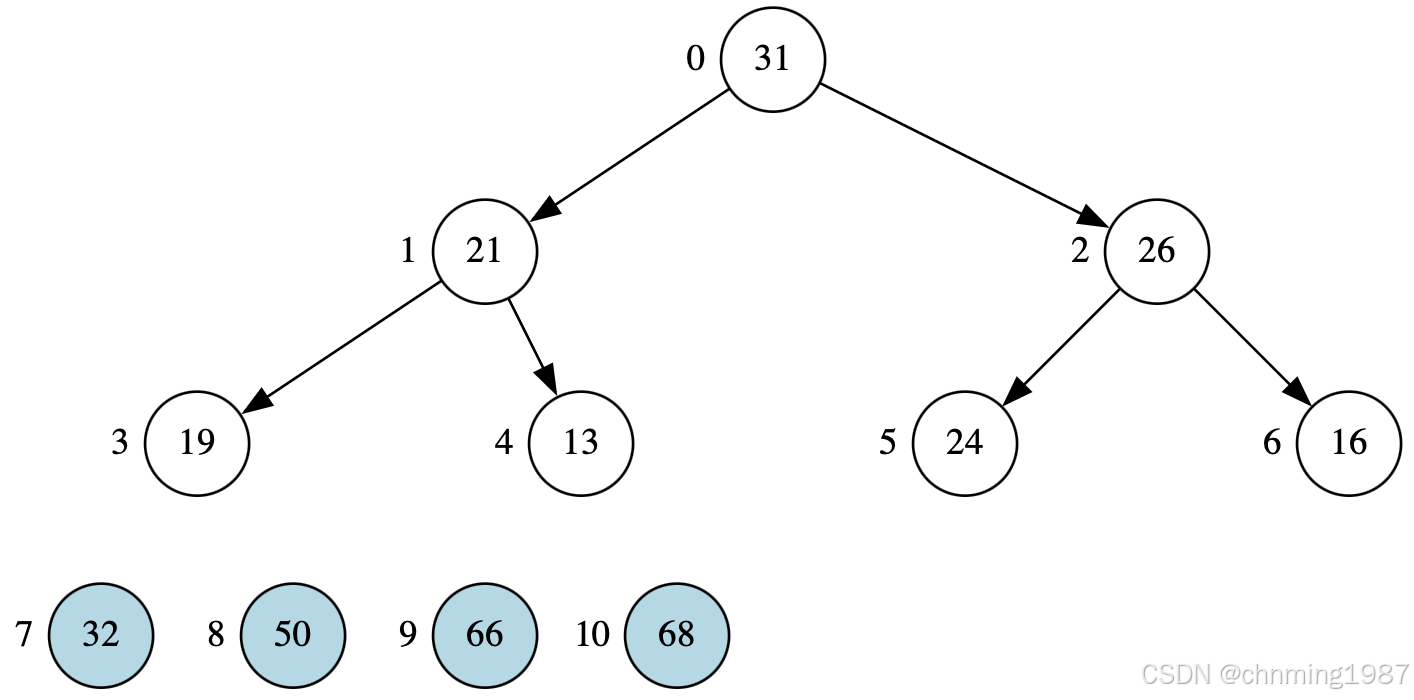
获取31，并调整堆

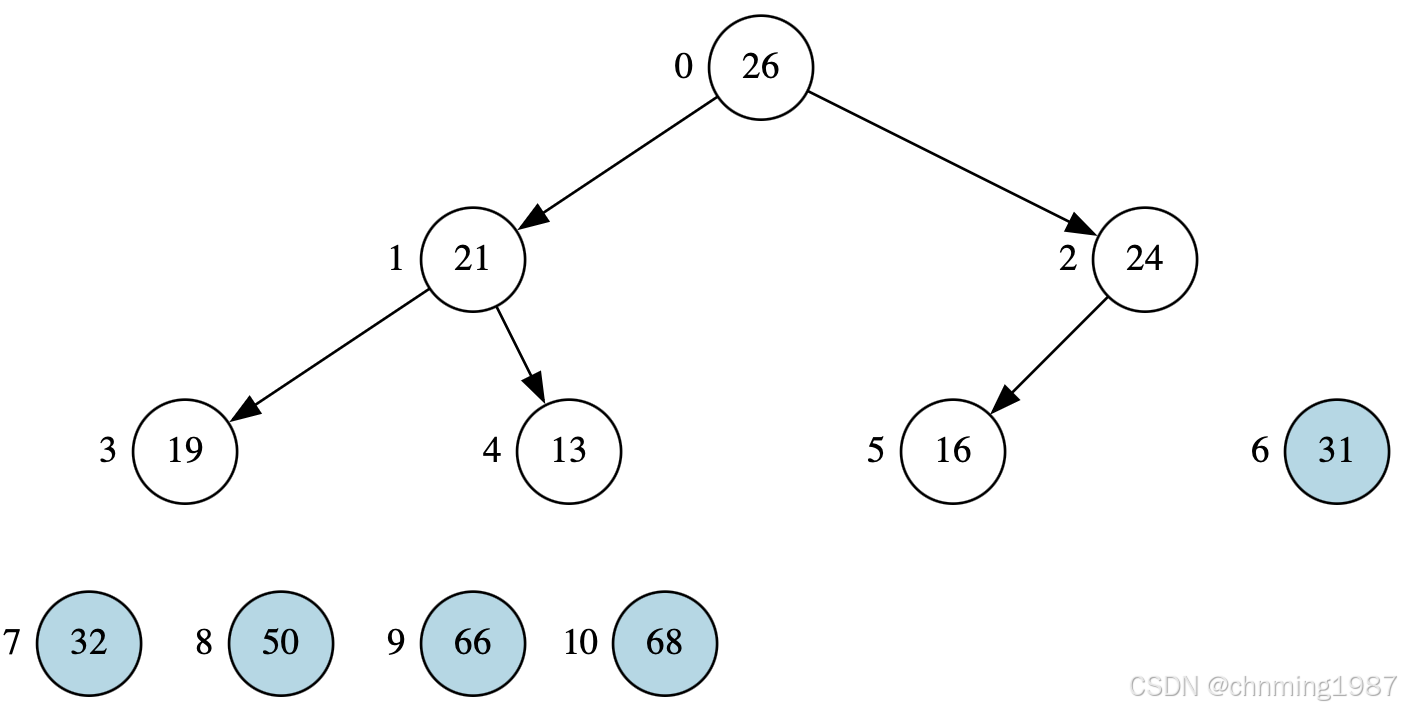
获取26，并调整堆

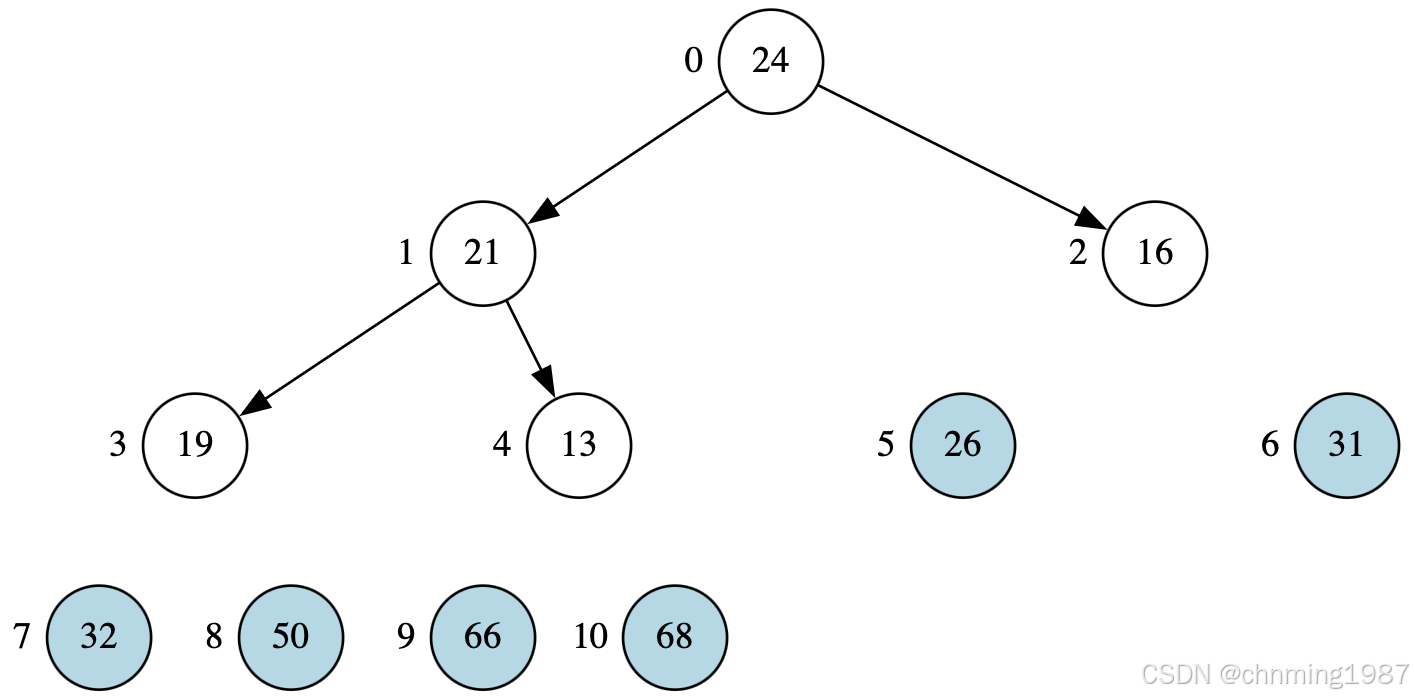
获取24，并调整堆

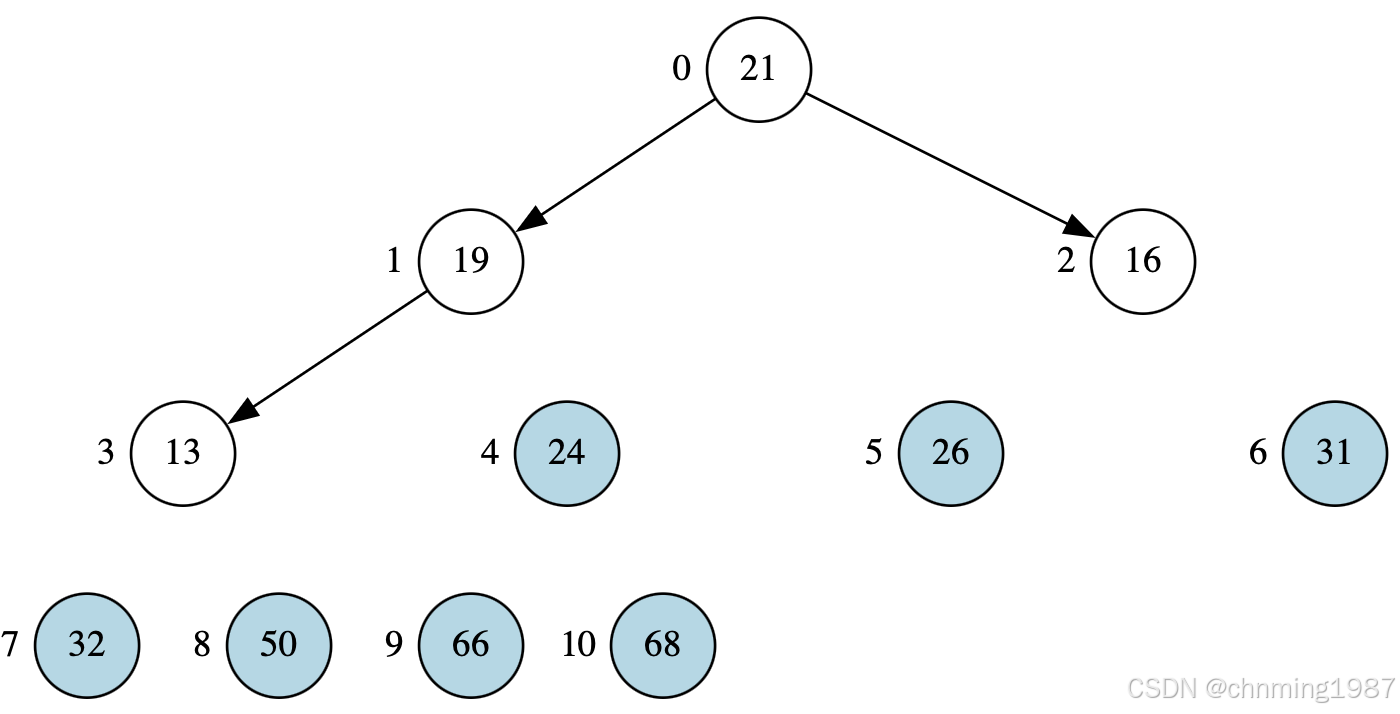
获取21，并调整堆

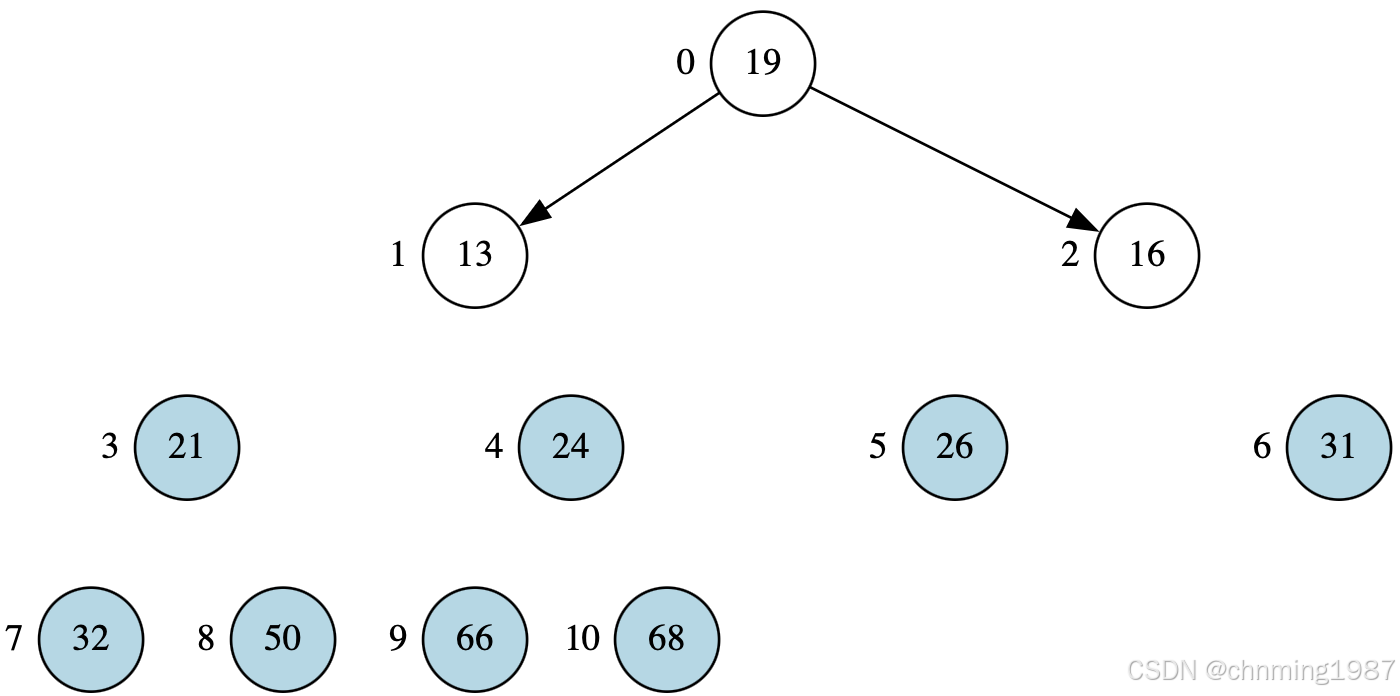
获取，19并调整堆

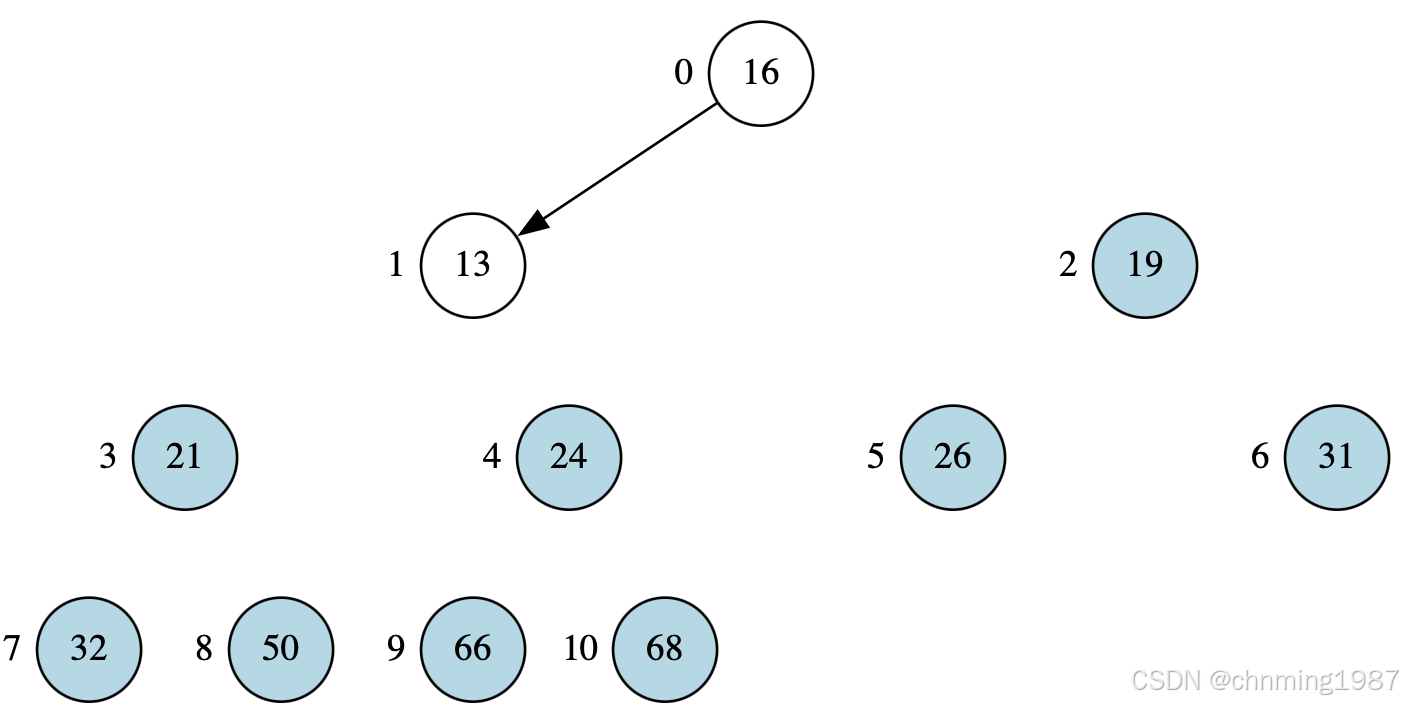
获取，16并调整堆

最终获得

图中，浅蓝色背景的节点为经过pop_heap并置为尾部的节点；

其代码如下：

template <class RandomAccessIterator>
void sort_heap(RandomAccessIterator first, RandomAccessIterator last) {
    while(last - first > 1) {
        pop_heap(first, last--);
    }
}

make_heap算法

这个算法用来将一段现有的数据转换为一个heap，其主要依据就是heap概述提到的complete binary tree的隐式表述（implicit representation）。

template<class RandomAccessIterator>
inline void make_heap(RandomAccessIterator first RandomAccessIterator last) {
    __make_heap(first, last, value_type(first), distance_type(first));   
}

template <class RandomAccessIterator, class T, class Distance>
void __make_heap(RandomAccessIterator first, RandomAccessIterator last, T*, Distance *) {
    if (last - first < 2 ) return ;
    Distance len = last - first;
    Distance parent = (len - 2) / 2;
    while(true) {
        __adjust_heap(first, parent, len, T(*(first + parent));
        if (parent == 0) return ;
        parent--;
    }
}

通过make_heap并不返回一个heap对象；而是将底层存储容器的排列变成了heap；所以没有针对heap的迭代器，需要从大到小遍历元素，最终还是使用底层容器的迭代器。

参考文档《STL源码剖析--侯捷》