单向散列函数-优快云博客

一、单向散列函数

首先，我们从名字上一眼就能看出来单向散列函数有两个关键修饰词，“单向”和“散列”

其实，在数学上，单向函数和散列函数是两个不同类型的函数，所以，我们要想理解单向散列函数，我们就要先区分清楚什么是单向函数，什么又是散列函数

1、单向函数

单向函数（One-way Function）是正向计算容易，逆向运算困难的函数，也就是说，给定一个输入，你很容易就计算出输出，但是给定一个输出，你却很难计算出输入是什么

注意是”逆向运算困难“而非”不能逆向运算“，可能性很小，但不是没有，密码理论领域里的很多棘手问题和密码应用领域里的很多错误都是源于单向函数的这种不确定性，每一个被破解的单向散列函数的密码学算法，在它被发明的时候，人们都找不到逆向运算的办法，可是在被破解的时候，人们就会发现原来还是有办法逆向运算的，在大家看来今天还是安全的算法，明天可能就被破解了，不过需要注意的是，我们要对这种不确定性保持足够的警惕，采取足够的防范措施，例如一个应用程序，至少要支持两种单向函数，当一种出现问题时，另一种可以替补

那对于我们来说，什么样的单向函数会更实用
1）正向计算会更容易，容易程度就是这个函数的计算性能
2）逆向运算会更困难，困难程度就是这个函数的破解强度
我还是要在此强调下，一个实用的单向函数，计算强度和破解强度需要均衡考量，不可偏废

2、散列函数

散列函数（Hash Function）是一个可以把任意长度的数据，转换成固定长度数据的函数，比如说，无论输入数据是 1 字节，还是 100 字节，输出数据都是 16 字节，我们把转换后的数据叫做散列值。因为散列函数经常被大家直译为哈希函数，所以我们也可以称散列值为哈希值，在输入数据和散列函数相同的情况下，散列值也是相同的

引申出一个问题，既然输入数据的长度没有限制，而输出数据的长度又是固定的，那么就一定会存在散列值相同的两个或者多个输入数据，通常，我们把这一现象称为散列值碰撞，理论上，我们是无法避免散列值碰撞的，只能把这种可能性降低，两个最直接的办法：
1）增大散列值长度，散列值长度越长，存在相同散列值的概率就越小，进而发生碰撞的可能性就越低，但与此同时也会带来弊端，散列值越长，通常也就意味着计算越困难，计算性能也就越差，那当初我们为什么要使用固定长度的散列值？不就是为了减少计算本身的性能损耗，从而获得性能优化嘛，所以，散列值并不是越长越好，散列值的长度应该是权衡性能后的一个结果
2）一个好的散列函数，它的散列值应该是均匀分布的，也就是说，每个散列值出现的概率都是一样的，否则的话，一部分散列值出现的概率就会较高，另一部分散列值出现的概率会较低，攻击者就更容易构造出两个或者多个数据，使得它们具有相同的散列值，这种行为称作碰撞攻击

3、单向散列函数

单向散列函数既是一个单向函数，也是一个散列函数，既要逆向运算困难，又要构造碰撞困难

构造碰撞困难，以 SHA-1 算法为例：

SHA-1("Hello, world!):
10010100 00111010 01110000 00101101 
00000110 11110011 01000101 10011001 
10101110 11100001 11111000 11011010 
10001110 11111001 11110111 00101001 
01100000 00110001 11010110 10011001

SHA-1("Hello, vorld!):
11001011 11111111 11111011 10010011 
01010111 11000010 10001101 01011000 
00100010 11000100 01010110 10000110 
00101010 00110011 01010000 10111110 
10000010 01111111 00100000 10101010

注意，‘w’(01110111) 和 ‘v’(01110110) 仅有 1 比特位上的差异，但计算出的散列值差异还是非常大的，这一现象称为雪崩效应

雪崩效应（Avalanche Effect）是密码学算法中的一个常见特点，指的是输入数据的细微改变，都会导致输出数据的巨变
严格雪崩准则（Strict Avalanche Criterion，SAC）是雪崩效应的一个形式化指标，我们也常用来衡量均匀分布，指的是输入数据有一位发生反转，输出数据的每一位都会有 50% 的概率发生变化

一个适用于密码学的单向散列函数，就要具有雪崩效应的特点，也就是说，如果一个单向散列函数具有雪崩效应，那么对于给定的数据，构造出一个新的、具有相同散列值的数据是困难的

二、单向散列函数如何保证数据完整性（完整性是防止未授权的修改数据，也就是：“不能改”）

假如我们收到了一段数据，我们可以计算出这段数据的散列值，假如我们还可以收到数据发送者计算出的散列值，就可以通过比对自己计算出的散列值和接收到的散列值是否一致来保证接收到的数据是否完整，如果两个散列值相同，我们就可以认为这段数据是完整的；否则，这段数据就是被篡改过的，这里面依然有两个遗留问题，也是我们使用单向散列函数需要特别关注的两个问题：
1）我们该选择什么样的单向散列函数？它的破解难度足够大到我们有信心根据计算出的散列值判断数据的完整性
2）我们怎么能够安全地接收到数据发送者计算的散列值？如果我们接收到的数据和散列值都是被修改过的，这样的话我们依旧不能判断接收到的数据是否被篡改过

1、问题一-SHA256/SHA384/SHA512

如何选择单向散列函数

2、问题二-对称密钥

为什么需要对称密钥？
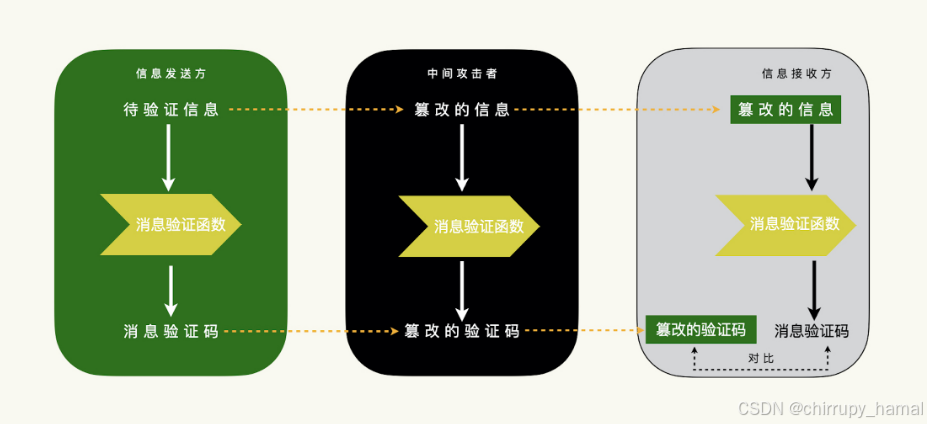
在这里插入图片描述
发送方把待验证信息和消息验证码发给接收方，假设存在一个中间攻击者，能够解开待验证信息和消息验证码，由于单向散列函数是公开的算法，攻击者就可以篡改待验证信息，并重新生成消息验证码，然后，攻击者把篡改的信息和验证码转发给接收方，被篡改的信息和验证码也能通过接收方的验证，这样的话，信息验证就失效了，也就是说，接收方是没有办法识别出接收到的信息是否被篡改过