哈工大 算法设计与分析（三）

算法一

        最优二分搜索树

        最优二分搜索树的动态规划算法确实是一个多项式时间算法。二分搜索树是一种常见的数据结构，用于在有序数据集中进行高效的搜索操作。而最优二分搜索树则是在给定数据集和搜索概率分布的情况下，构建出搜索代价最小的二分搜索树。

动态规划是一种解决最优化问题的有效方法，通过将问题分解为子问题并存储子问题的解，避免了重复计算，从而提高了算法的效率。在最优二分搜索树的构建过程中，我们可以使用动态规划算法来找到最优解。

具体来说，我们可以定义一个二维数组dp，其中dp[i][j]表示在数据集的第i个元素到第j个元素之间构建最优二分搜索树的最小搜索代价。然后，我们可以使用动态规划的思想，通过填充这个数组来逐步找到最优解。

在填充数组的过程中，我们需要考虑每个可能的根节点，并计算以该节点为根节点的子树的最小搜索代价。通过遍历所有可能的根节点，我们可以找到整个数据集上的最优二分搜索树。

由于动态规划算法的时间复杂度通常与问题的规模呈多项式关系，因此最优二分搜索树的动态规划算法也是一个多项式时间算法。这意味着对于任何给定规模的问题，我们都可以在合理的时间内找到最优解。

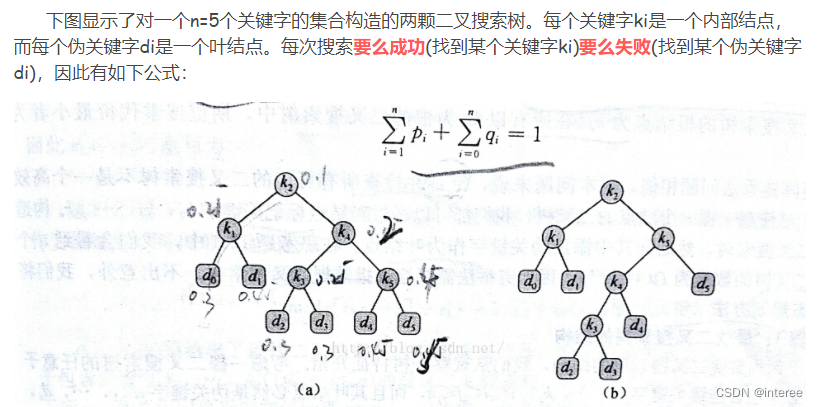
引用：《算法导论》之最优二叉搜索树_最优二叉搜索树例题-优快云博客

算法二

        树形DP：树的最大独立集

例题： 引用自：树形DP：树的最大独立集_cwbc和xhrlyb生活在 s 市,这天他们打算一起出去旅游。 旅行地图上有 n 个城市-优快云博客

Cwbc和XHRlyb生活在 s 市，这天他们打算一起出去旅游。
旅行地图上有 n 个城市，它们之间通过 n-1 条道路联通。
Cwbc和XHRlyb第一天会在 s 市住宿，并游览与它距离不超过 1 的所有城市，之后的每天会选择一个城市住宿，然后游览与它距离不超过 1 的所有城市。
一个已经浏览过的城市不会在居住。
最多能度过多少天的时光？

输入描述：

第一行，两个正整数n和s，表示城市个数和第一天住宿的城市s。
接下来n-1行，每行两个整数x和y，表示城市x与城市y之间有一条双向道路。
输出描述：
第一行，一个非负整数表示答案。

示例1
输入：
4 1
1 2
2 3
3 4
输出：
2
说明：
第一天，在1号城市住宿，游览了1、2号城市。
第二天，在3号城市住宿，游览了4号城市，旅行结束。

求解思路：

典型的树的遍历问题，对于任意一个树中的节点，其可以选择加入到最大独立集中，或者不加入到独立集合中，有：

• dp[u][0]+=max(dp[v][0],dp[v][1])
  即当前节点不加入到独立集，那么其相邻节点（儿子节点），可以加入，或者不加入
• dp[u][1]+=dp[v][0] 即当前节点加入到独立集，那么其相邻节点（儿子节点）不加入

#include <bits/stdc++.h>

using namespace std;

const int N = 1e6 + 5;
typedef long long LL;
int n, s,dp[N][2];
vector<int> mp[N];

void dfs(int now, int fa) {
   //研究其子节点
    for (int i = 0; i < mp[now].size(); i++) {
       //记录节点序号
        int ne = mp[now][i];
        //避免环路
        if (ne == fa) continue;
        //先完成子问题的求解
        dfs(ne, now);
        //当前节点选择，那么一定对应于其相连节点不选择
        dp[now][1] += dp[ne][0];
        //当前节点不选择，那么其儿子节点可以选，也可以不选，取最大值
        dp[now][0] += max(dp[ne][0], dp[ne][1]);
    }
    dp[now][1]++;
}

int main() {
   
    cin >> n >> s;
    for (int i = 0; i < n - 1; i++) {
   
        int x, y;
        cin >> x >> y;
        mp[x].push_back(y);
        mp[y].push_back(x);
    }
    dfs(s, 0);
    cout << dp[s][1] << endl;
    return 0;
}

        树上的最大独立集合问题是一个经典的组合优化问题。关于它是否为NP完全问题，实际上，树上的最大独立集合问题并不是NP完全的，而是可以在多项式时间内解决的。这是因为它具有树形结构，我们可以利用这个特性设计高效的算法来找到最大独立集合。通常，NP完全问题指的是那些即使在理想情况下也没有已知多项式时间解法的问题，而树上的最大独立集合问题并不属于这一类别。所以，我们可以放心地说，树上的最大独立集合问题不是NP完全问题。

图的最大独立集合问题之所以是NP完全问题，主要是因为它具有NP完全问题的两个关键特征：问题的验证可以在多项式时间内完成，且该问题可以被归约到其他已知的NP完全问题。

首先，关于验证部分，给定一个图的独立集合，验证它是否是一个最大独立集合是相对容易的。这是因为验证过程只需检查集合中的每个顶点，确保它们之间没有边相连，并且集合的大小不小于任何其他独立集合。这个验证过程的时间复杂度是图顶点数量的线性函数，因此是多项式时间的。

其次，最大独立集合问题可以通过归约的方式与已知的NP完全问题相联系。归约是证明一个问题是NP完全的一种常用方法，它通过将一个已知的NP完全问题转化为另一个问题来证明后者的NP完全性。在最大独立集合问题的情况下，它可以被归约到诸如“顶点覆盖”或“集合覆盖”等已知的NP完全问题。这些归约过程展示了最大独立集合问题至少和这些已知的NP完全问题一样难解。

最后，值得注意的是，虽然最大独立集合问题是NP完全的，但这并不意味着对于所有图，找到最大独立集合都是困难的。对于某些特殊的图类，如二分图，存在多项式时间的算法可以找到最大独立集合。然而，对于一般的图，目前尚未发现多项式时间的算法来解决最大独立集合问题，因此它被认为是NP完全的。

综上所述，图的最大独立集合问题之所以是NP完全问题，是因为它的验证可以在多项式时间内完成，并且它可以通过归约的方式与已知的NP完全问题相联系。这意味着，除非P=NP（这是一个尚未解决的数学问题），否则我们不可能找到一个多项式时间的算法来求解所有图的最大独立集合问题。

 

算法三

        任意两点最短路径问题--Floyd算法

详细：弗洛伊德（Floyd)算法详解_floyd算法-优快云博客