MathML学习：几个高等数学公式的MathML源码

最新推荐文章于 2025-09-16 01:55:21 发布

转载最新推荐文章于 2025-09-16 01:55:21 发布 · 1.6k 阅读

2 ·

CC 4.0 BY-SA版权

原文链接：https://my.oschina.net/Tsybius2014/blog/397618

本文介绍了学习MathML的过程，通过Amaya工具创建数学公式，并以勾股定理、欧拉公式等高等数学例子展示MathML源码。推荐使用Firefox预览MathML文件，同时分享了字符查找技巧和文件扩展名对显示效果的影响。

今天我研究了下数学标记语言MathML。于是我把我大学毕业后扔掉了好久的高数书又捡了回来，找了几个公式实现了下。并记下了它们的代码，并总结了些心得体会，方便日后查阅。

一、我的方法

1）我使用了Amaya11.4.7帮我构建数学公式，点击“File”菜单下的“New”，找到“New formula...”。

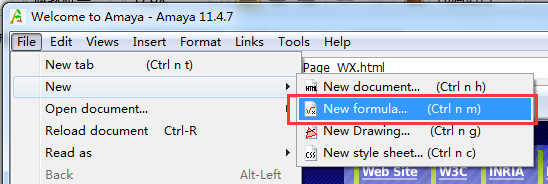
2）指定一个位置保存我们要编辑的mml文件，字符集选择默认的“iso-8859-1”，这是由国际标准化组织内定义的一个8位字符集。

3）编辑公式，保存文件。

4）可以用火狐浏览器（Firefox）打开保存好的mml文件预览效果。也可以使用任何文本编辑工具打开mml文件查看源码。

现在有个mml文件，源码如下：

<?xml version="1.0" encoding="iso-8859-1"?>
<!DOCTYPE math PUBLIC "-//W3C//DTD MathML 2.0//EN"
      "http://www.w3.org/TR/MathML2/dtd/mathml2.dtd">
<!-- Created by amaya 11.4.7, see http://www.w3.org/Amaya/ -->
<math xmlns="http://www.w3.org/1998/Math/MathML">
  <mn>1</mn>
  <mo>+</mo>
  <mn>1</mn>
  <mo>=</mo>
  <mn>2</mn>
</math>

使用几个浏览器对mml文件打开后预览结果：

1）我使用的Firefox版本为“37.0.1”，用Firefox打开mml文件后，会显示如下预览结果：

2）我使用的IE版本为“8.0.7601.17514”，用IE打开mml文件后，会提示“文件下载”对话框（如下图）。由于我之前设定了mml文件默认用Firefox打开，所以点击了“文件下载”对话框中的“打开”按钮后，会用Firefox打开mml文件。

3）我使用的Chrome版本为“41.0.2272.118 m”，打开mml文件后，Chrome会直接指出“语法错误”

综上所述，我还是选择了火狐浏览器作为mml的预览效果工具

二、公式1：勾股定理

1）Firefox下的预览效果

2）公式源码

<?xml version="1.0" encoding="iso-8859-1"?>
<!DOCTYPE math PUBLIC "-//W3C//DTD MathML 2.0//EN"
      "http://www.w3.org/TR/MathML2/dtd/mathml2.dtd">
<!-- Created by amaya 11.4.7, see http://www.w3.org/Amaya/ -->
<math xmlns="http://www.w3.org/1998/Math/MathML">
  <msup>
    <mi>a</mi>
    <mn>2</mn>
  </msup>
  <mo>+</mo>
  <msup>
    <mi>b</mi>
    <mn>2</mn>
  </msup>
  <mo>=</mo>
  <msup>
    <mi>c</mi>
    <mn>2</mn>
  </msup>
</math>

三、公式2：欧拉公式

1）Firefox下的预览效果

2）公式源码

<?xml version="1.0" encoding="iso-8859-1"?>
<!DOCTYPE math PUBLIC "-//W3C//DTD MathML 2.0//EN"
      "http://www.w3.org/TR/MathML2/dtd/mathml2.dtd">
<!-- Created by amaya 11.4.7, see http://www.w3.org/Amaya/ -->
<math xmlns="http://www.w3.org/1998/Math/MathML">
  <msup>
    <mi>e</mi>
    <mi>i&pi;</mi>
  </msup>
  <mo>+</mo>
  <mn>1</mn>
  <mo>=</mo>
  <mn>0</mn>
</math>

四、公式3：重要极限（一个极值为e的极限）

1）Firefox下的预览效果

2）公式源码

<?xml version="1.0" encoding="iso-8859-1"?>
<!DOCTYPE math PUBLIC "-//W3C//DTD MathML 2.0//EN"
      "http://www.w3.org/TR/MathML2/dtd/mathml2.dtd">
<!-- Created by amaya 11.4.7, see http://www.w3.org/Amaya/ -->
<math xmlns="http://www.w3.org/1998/Math/MathML">
  <mrow>
    <munder>
      <mo>lim</mo>
      <mrow>
        <mi>n</mi>
        <mo>&rarr;</mo>
        <mi>&infin;</mi>
      </mrow>
    </munder>
    <msup>
      <mrow>
        <mo>(</mo>
        <mn>1</mn>
        <mo>+</mo>
        <mfrac>
          <mn>1</mn>
          <mi>n</mi>
        </mfrac>
        <mo>)</mo>
      </mrow>
      <mi>n</mi>
    </msup>
  </mrow>
  <mo>=</mo>
  <mi>e</mi>
  <mo>.</mo>
</math>

五、公式4：参数方程（x=x(t); y=y(t)）的曲率

1）Firefox下的预览效果

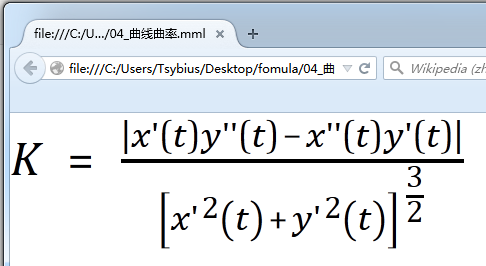
2）公式源码

<?xml version="1.0" encoding="iso-8859-1"?>
<!DOCTYPE math PUBLIC "-//W3C//DTD MathML 2.0//EN"
      "http://www.w3.org/TR/MathML2/dtd/mathml2.dtd">
<!-- Created by amaya 11.4.7, see http://www.w3.org/Amaya/ -->
<math xmlns="http://www.w3.org/1998/Math/MathML">
  <mi>K</mi>
  <mo>=</mo>
  <mfrac>
    <mrow>
      <mo>&#x2223;</mo>
      <mrow>
        <mi>x</mi>
        <mo>'</mo>
        <mo>(</mo>
        <mi>t</mi>
        <mo>)</mo>
        <mi>y</mi>
        <mo>'</mo>
        <mo>'</mo>
        <mo>(</mo>
        <mi>t</mi>
        <mo>)</mo>
        <mo>&minus;</mo>
        <mi>x</mi>
        <mo>'</mo>
        <mo>'</mo>
        <mo>(</mo>
        <mi>t</mi>
        <mo>)</mo>
        <mi>y</mi>
        <mo>'</mo>
        <mo>(</mo>
        <mi>t</mi>
        <mo>)</mo>
      </mrow>
      <mo>&#x2223;</mo>
    </mrow>
    <msup>
      <mrow>
        <mo>[</mo>
        <msup>
          <mrow>
            <mi>x</mi>
            <mo>'</mo>
          </mrow>
          <mn>2</mn>
        </msup>
        <mo>(</mo>
        <mi>t</mi>
        <mo>)</mo>
        <mo>+</mo>
        <msup>
          <mrow>
            <mi>y</mi>
            <mo>'</mo>
          </mrow>
          <mn>2</mn>
        </msup>
        <mo>(</mo>
        <mi>t</mi>
        <mo>)</mo>
        <mo>]</mo>
      </mrow>
      <mfrac>
        <mn>3</mn>
        <mn>2</mn>
      </mfrac>
    </msup>
  </mfrac>
</math>

六、公式5：向量s=(m,n,p)与法向量为n=(A,B,C)的平面夹角

1）Firefox下的预览效果

2）公式源码

<?xml version="1.0" encoding="iso-8859-1"?>
<!DOCTYPE math PUBLIC "-//W3C//DTD MathML 2.0//EN"
      "http://www.w3.org/TR/MathML2/dtd/mathml2.dtd">
<!-- Created by amaya 11.4.7, see http://www.w3.org/Amaya/ -->
<math xmlns="http://www.w3.org/1998/Math/MathML">
  <mrow>
    <mi>sin</mi>
    <mo>&#x2061;</mo>
    <mi>&theta;</mi>
  </mrow>
  <mo>=</mo>
  <mfrac>
    <mrow>
      <mo>&#x2223;</mo>
      <mrow>
        <mi>A</mi>
        <mi>m</mi>
        <mo>+</mo>
        <mi>B</mi>
        <mi>n</mi>
        <mo>+</mo>
        <mi>C</mi>
        <mi>p</mi>
      </mrow>
      <mo>&#x2223;</mo>
    </mrow>
    <mrow>
      <msqrt>
        <msup>
          <mi>A</mi>
          <mn>2</mn>
        </msup>
        <mo>+</mo>
        <msup>
          <mi>B</mi>
          <mn>2</mn>
        </msup>
        <mo>+</mo>
        <msup>
          <mi>C</mi>
          <mn>2</mn>
        </msup>
      </msqrt>
      <msqrt>
        <msup>
          <mi>m</mi>
          <mn>2</mn>
        </msup>
        <mo>+</mo>
        <msup>
          <mi>n</mi>
          <mn>2</mn>
        </msup>
        <mo>+</mo>
        <msup>
          <mi>p</mi>
          <mn>2</mn>
        </msup>
      </msqrt>
    </mrow>
  </mfrac>
  <mo>.</mo>
</math>

七、公式6：以2π为周期的傅里叶级数

1）Firefox下的预览效果

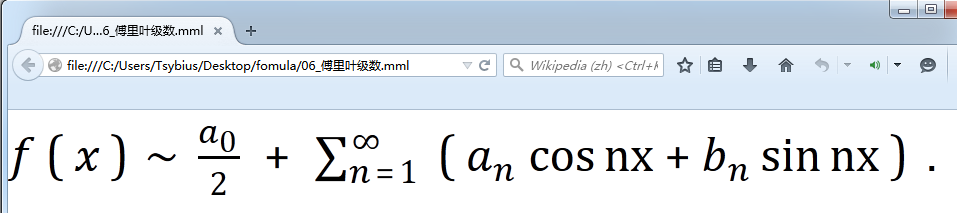
其中：

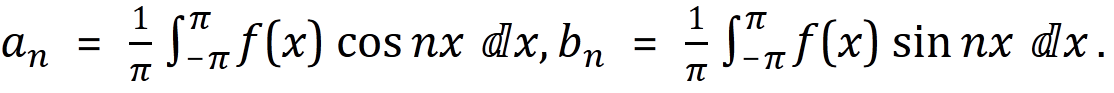
2）公式源码

上图：

<?xml version="1.0" encoding="iso-8859-1"?>
<!DOCTYPE math PUBLIC "-//W3C//DTD MathML 2.0//EN"
      "http://www.w3.org/TR/MathML2/dtd/mathml2.dtd">
<!-- Created by amaya 11.4.7, see http://www.w3.org/Amaya/ -->
<math xmlns="http://www.w3.org/1998/Math/MathML">
  <mi>f</mi>
  <mo>(</mo>
  <mi>x</mi>
  <mo>)</mo>
  <mo>~</mo>
  <mfrac>
    <msub>
      <mi>a</mi>
      <mn>0</mn>
    </msub>
    <mn>2</mn>
  </mfrac>
  <mo>+</mo>
  <munderover>
    <mo>&sum;</mo>
    <mrow>
      <mi>n</mi>
      <mo>=</mo>
      <mn>1</mn>
    </mrow>
    <mi>&infin;</mi>
  </munderover>
  <mo>(</mo>
  <msub>
    <mi>a</mi>
    <mi>n</mi>
  </msub>
  <mrow>
    <mi>cos</mi>
    <mo>&#x2061;</mo>
    <mi>nx</mi>
    <mo>+</mo>
    <mrow>
      <msub>
        <mi>b</mi>
        <mi>n</mi>
      </msub>
      <mi>sin</mi>
      <mo>&#x2061;</mo>
      <mi>nx</mi>
    </mrow>
  </mrow>
  <mo>)</mo>
  <mo>.</mo>
</math>

下图：

<?xml version="1.0" encoding="iso-8859-1"?>
<!DOCTYPE math PUBLIC "-//W3C//DTD MathML 2.0//EN"
       "http://www.w3.org/TR/MathML2/dtd/mathml2.dtd">
<!-- Created by amaya 11.4.7, see http://www.w3.org/Amaya/ -->
<math xmlns="http://www.w3.org/1998/Math/MathML">
  <msub>
    <mi>a</mi>
    <mi>n</mi>
  </msub>
  <mo>=</mo>
  <mfrac>
    <mn>1</mn>
    <mi>&pi;</mi>
  </mfrac>
  <mrow>
    <msubsup>
      <mo>&int;</mo>
      <mrow>
        <mo>&minus;</mo>
        <mi>&pi;</mi>
      </mrow>
      <mi>&pi;</mi>
    </msubsup>
    <mrow>
      <mi>f</mi>
      <mo>(</mo>
      <mi>x</mi>
      <mo>)</mo>
    </mrow>
  </mrow>
  <mrow>
    <mi>cos</mi>
    <mo>&#x2061;</mo>
    <mrow>
      <mi>n</mi>
      <mi>x</mi>
    </mrow>
  </mrow>
  <mrow>
    <mo>&#x2146;</mo>
    <mi>x</mi>
    <mo>,</mo>
    <msub>
      <mi>b</mi>
      <mi>n</mi>
    </msub>
  </mrow>
  <mo>=</mo>
  <mfrac>
    <mn>1</mn>
    <mi>&pi;</mi>
  </mfrac>
  <mrow>
    <msubsup>
      <mo>&int;</mo>
      <mrow>
        <mo>&minus;</mo>
        <mi>&pi;</mi>
      </mrow>
      <mi>&pi;</mi>
    </msubsup>
    <mrow>
      <mi>f</mi>
      <mo>(</mo>
      <mi>x</mi>
      <mo>)</mo>
    </mrow>
  </mrow>
  <mrow>
    <mi>sin</mi>
    <mo>&#x2061;</mo>
    <mrow>
      <mi>n</mi>
      <mi>x</mi>
    </mrow>
  </mrow>
  <mrow>
    <mo>&#x2146;</mo>
    <mi>x</mi>
    <mo>.</mo>
  </mrow>
</math>

八、几点心得体会

1）对于一些数学、物理上使用，但又不好找的特殊字符，如“Ĥ”、“ħ”等，可以参考英语的维基词典条目

如与字母h相关的字符，可以去下面页面查找：http://en.wiktionary.org/wiki/Appendix:Variations_of_%22h%22

其中两个“%22”中的字符，即为要找的字符，在维基词典中，可以找到字母h的若干变体：

2）需要注意的是，同样的代码，扩展名不同，用Firefox打开后的结果也可能不同

比如下面是一段我从互联网上粘下来的代码：

（粘自页面：http://www.ibm.com/developerworks/cn/xml/x-mathml/）

<math xmlns="http://www.w3.org/1998/Math/MathML">
      <msup>
        <mi>n</mi>
    <mrow>
         <mi>p</mi>
      <mo>-</mo>
          <mn>1</mn>
    </mrow>
  </msup>
  <mspace width=".2em"/>
  <mo>&equiv;</mo>
  <mspace width=".2em"/>
  <mn>1</mn>
  <mspace width=".2em"/>
  <mo>(</mo>
  <mi>mod</mi>
  <mspace width=".2em"/>
  <mi>p</mi>
  <mo>)</mo>
</math>

我将它保存到temp.html中，用Firefox打开，预览如下：

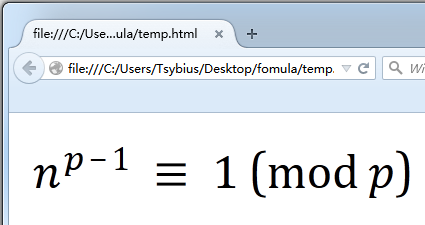
但我将它改名为temp.mml后，用Firefox就不能正确显示了：

问题就出在“&equiv;”上，必须把它改成“≡”，这才是MathML里显示字符“≡”的方式。

END

转载于:https://my.oschina.net/Tsybius2014/blog/397618