一、介绍
回顾以下以前 value-based的方法:在value-based方法中,他们都是去学习一个动作的价值函数,然后根据这个动作的价值函数作出下一步选择。以至于这个方法高度依赖动作价值函数,如果没有动作价值函数,也就不知道如何为下一步作出抉择。
在本文中,我们提出一种新的想法来解决Reinforcement Learning 中的决策问题。即直接去训练这么一个策略,它能直接给出下一步动作是什么。当然,这个策略肯定是带参数的。我们最直接的目标就是优化策略的参数,使之能够很好的做出准确的决策。换句话说,以前 value-based方法是找出每一个状态下的每一个动作的价值函数,而 Policy Gradient 的方法是找出每一个状态下该采取哪个动作的函数。前者是 状态动作到价值的映射,后者是状态到动作的映射。显然后者更简单粗暴点。后者这种方法就叫做policy-based.
为了表示出Policy Gradient中的策略,我们记 θ\thetaθ 为策略的参数向量。因此策略可以用如下概率表示:
π(a∣s,θ)=Pr{At=a∣Ss,θt=θ}\pi(a|s, \theta) = Pr\{A_t = a | S_s, \theta_t = \theta\}π(a∣s,θ)=Pr{At=a∣Ss,θt=θ}
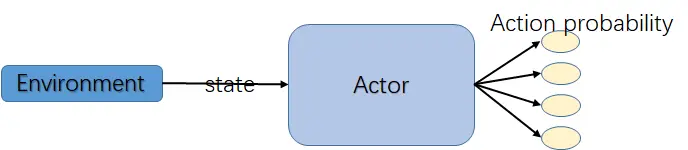
即在时间 t 时,在状态 s 下选取某一个动作的概率。
实际上,我们定义了一个某一个状态下关于动作的概率分布。有了这个概率分布,决策时在这个分布中采样就可以了。
当然policy gradient 也可以处理连续空间问题,如下图所示,但本文主要以离散动作空间做例子:
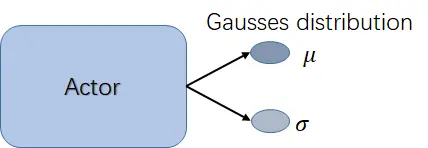
二、优化策略
OK,那问题来了,策略 π(a∣s,θ)\pi(a|s, \theta)π(a∣s,θ) 有了,该怎么优化这个策略呢?如果能找到最优的策略,那不管环境给你怎样的状态,我们都能从策略中得到当前状态下关于动作的分布,最后采样结果就是抉择的结果。但是前提是这个策略是靠谱的,所以我们下面研究如何优化这个策略。
这里要提出一个优化方法:梯度下降。
首先,我们要有一个衡量策略结果好坏的函数,把它叫做目标函数,记 J(θ)J(\theta)J(θ),其中θ\thetaθ是参数向量。这个目标函数值越大,说明我们的策略越好,反之越差。所以实际上问题就转化为最大化目标函数。而最大化该函数的方法就是用梯度下降。
应用梯度下降方法求解最大化函数问题,简单地讲就是求偏导,最后的参数更新有如下形式:
θt+1=θt+α∇J(θt)\theta_{t+1} = \theta_t + \alpha \nabla J(\theta_t)θt+1=θt+α∇J(θt)
这个一个非常一般的一种形式,不同的目标函数催生出不同的算法。但是,只要可以表示成上面这种形式的表达式,都属于 Policy Gradient 方法。
那么,该怎么计算 ∇J(θ)\nabla J(\theta)∇J(θ) 以及 π(a∣s,θ)=Pr{At=a∣Ss,θt=θ}\pi(a|s, \theta) = Pr\{A_t = a | S_s, \theta_t = \theta\}π(a∣s,θ)=Pr{At=a∣Ss,θt=θ}呢?
实际上,这两个的计算方法都依赖于其本身的定义。例如:对于离散动作空间下,策略π\piπ可以用 soft-max 分布表示
π(a∣s,θ)=eh(s,a,θ)∑beh(s,b,θ)\pi(a|s, \theta) = \frac{e^{h(s, a, \theta)}}{\sum_b e^{h(s, b, \theta)}}π(a∣s,θ)=∑beh(s,b,θ)eh(s,a,θ)
其中h(s,a,θ)h(s, a, \theta)h(s,a,θ)是状态-动作对的参数化表示,可以用一个神经网络去近似它:
h(s,a,θ)=θTx(s,a)h(s,a, \theta) = \theta^T x(s,a)h(s,a,θ)=θTx(s,a)
其中 θ\thetaθ 是网络中去权重的向量,x(s,a)x(s,a)x(s,a)表示状态和动作的特征。
至于如何计算 ∇J(θ)\nabla J(\theta)∇J(θ)? 计算前必须先定义好 J(θ)J(\theta)J(θ)。假设环境能产生一段完整的 episode, 那么我们可以用初始状态的价值去表示目标函数:
J(θ)=vπθ(s0)J(\theta) = v_{\pi_\theta}(s_0)J(θ)=vπθ(s0)
对J(θ)=vπθ(s0)J(\theta) = v_{\pi_\theta}(s_0)J(θ)=vπθ(s0) 求偏导,其偏导结果有定理Policy Gradient Theorem给出
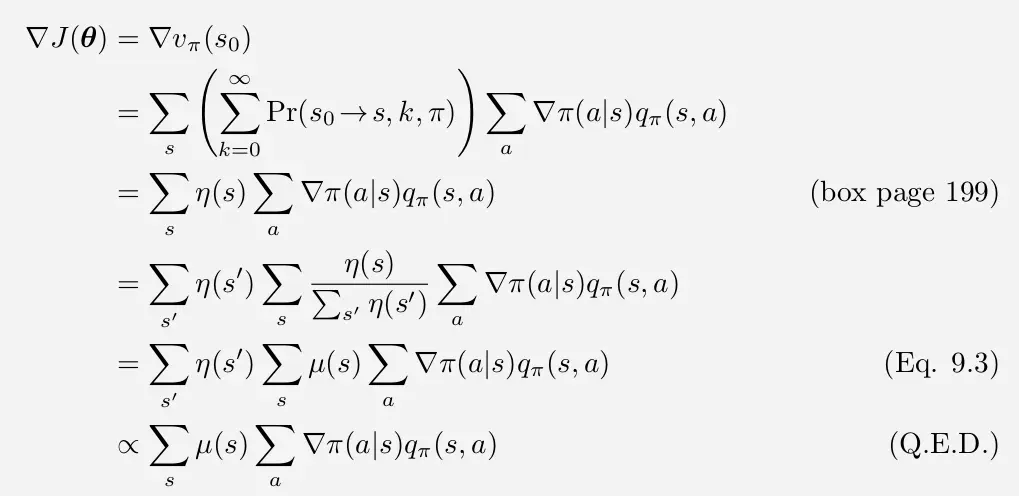
有了上面的求导结果,就可以导出第一个 policy-gradient 算法了:Monte Carlo Policy Gradient
从上面公式看,∇J(θ)\nabla J(\theta)∇J(θ) 结果与 ∑μ(s)∑a∇π(a∣s)qπ(s,a)\sum \mu (s) \sum_a \nabla \pi (a|s) q_\pi (s,a)∑μ(s)∑a∇π(a∣s)qπ(s,a) 成正比,进一步写成:
∇J(θ)∝∑μ(s)∑a∇π(a∣s)qπ(s,a)\nabla J(\theta) \propto \sum \mu (s) \sum_a \nabla \pi (a|s) q_\pi (s,a)∇J(θ)∝∑μ(s)a∑∇π(a∣s)qπ(s,a)
=Eπ[∑aqπ(St,a)∇π(a∣St,θ)] = E_\pi[ \sum_a q_\pi (S_t , a) \nabla \pi (a|S_t, \theta)]=Eπ[a∑qπ(St,a)∇π(a∣St,θ)]
实际上我们可以把∇J(θ)\nabla J(\theta)∇J(θ) 和 ∑μ(s)∑a∇π(a∣s)qπ(s,a)\sum \mu (s) \sum_a \nabla \pi (a|s) q_\pi (s,a)∑μ(s)∑a∇π(a∣s)qπ(s,a) 之间画上等号,因为我们在更新参数 θ\thetaθ 的时候会乘上一个学习数率α\alphaα,这个参数可以消去这两个项之间的比例系数。所以,放心画上等号后:
KaTeX parse error: No such environment: align at position 7: \begin{̲a̲l̲i̲g̲n̲}̲
\nabla J(\thet…
现在就能导出 monte carlo 的 policy gradient 的更新公式了:
θ(t+1)=θt+αGt∇π(At∣St,θ)\theta_(t+1) = \theta_t + \alpha G_t \nabla \pi(A_t | S_t , \theta)θ(t+1)=θt+αGt∇π(At∣St,θ)
三、算法框架
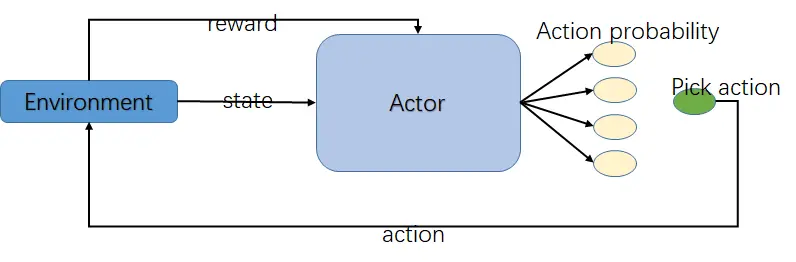
- 初始化状态 s0s_0s0
- 将状态 s0s_0s0 传入 RL 算法,得到各个动作的概率
- 根据概率分布采样,得到下一步动作 a0a_0a0
- 环境对 Agent 作出的动作 a0a_0a0 给予相应的奖励 r1r_1r1, Agent 到达下一个状态 s1s_1s1
经过上面步骤后,得到数据集: {s0,a0,r1,s1}\{s_0, a_0, r_1, s_1\}{s0,a0,r1,s1}, 如果 a0a_0a0 不是终止动作,上面的步骤还必须继续进行,直到遇到终止动作,一段 episode 就说是结束了。
最后收集的数据: {s0,a0,r1,s1,a1,r2,s2,......,sT−1,aT−1,rT,sT}\{ s_0, a_0, r_1, s_1, a_1, r_2, s_2 , ... ..., s_{T-1}, a_{T-1}, r_T, s_T \}{s0,a0,r1,s1,a1,r2,s2,......,sT−1,aT−1,rT,sT}
有了数据后才进行算法的更新。

这是 sutton 的《Reinforcement learning 》书中所叙的算法。下面再贴上 Devil 的算法:

这两个算法差别不大,可以说基本差不多。注意 Devil 版本的算法中的更新公式中有一项是vtv_tvt,这个vtv_tvt实际上还是用GtG_tGt去估计。





 本文深入探讨了强化学习中Policy Gradient方法的原理与实现。对比Value-Based方法,Policy Gradient直接学习策略函数,简化决策过程。文章详细介绍了策略的数学表示、优化策略的梯度下降方法及目标函数的设定。通过Monte Carlo Policy Gradient算法示例,展示了参数更新的具体过程。最后,提供了算法框架,包括状态转移、动作选择和参数更新的步骤。
本文深入探讨了强化学习中Policy Gradient方法的原理与实现。对比Value-Based方法,Policy Gradient直接学习策略函数,简化决策过程。文章详细介绍了策略的数学表示、优化策略的梯度下降方法及目标函数的设定。通过Monte Carlo Policy Gradient算法示例,展示了参数更新的具体过程。最后,提供了算法框架,包括状态转移、动作选择和参数更新的步骤。

















 1145
1145

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










