k-Wave 工具箱学习-1概述

炙搏温流

已于 2023-07-05 17:26:36 修改

阅读量2.1k

点赞数 2

CC 4.0 BY-SA版权

分类专栏： k-Wave教程文章标签： matlab 学习

于 2023-06-23 15:25:55 首次发布

原文链接：http://www.k-wave.org/documentation.php

k-Wave教程专栏收录该内容

5 篇文章

订阅专栏

k-Wave是一个MATLAB工具箱，用于一维、二维和三维声波场的时域模拟。文章介绍了如何使用kspaceFirstOrder函数进行声波仿真，涉及创建计算网格、定义声学介质（如异质声速）、设定声源和传感器。示例代码展示了如何配置这些参数并运行2D仿真，最终在每个时间步长获取传感器记录的声压数据。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

第3 章 First-Order SimulationFunctions

3.1 概述

注：文章讲解一些对工具箱使用的实操理论。文章内容全部来自k-Wave的官网手册官网链接k-Wave: A MATLAB toolbox for the time domain simulation of acoustic wave fields

k-Wave的示例代码和内置函数教程都在官网可以找到，以下为其他学习部分链接

第3 章 First-Order SimulationFunctions

3.1 概述

kspaceFirstOrder1D、kspaceFirstOrder2D 和 kspaceFirstOrder3D函数分别用于一维、二维、三维的声波仿真。

可使用四个matlab结构体（structure）作为输入参数调用模拟函数： kgrid, medium, source, 和sensor。这四个结构体分别定义了计算网格的属性、介质的材料属性、任何声源的属性和位置，以及用于记录压力场和粒子速度场在整个过程中演变的时域探针。四个structure的属性定义为 structure.field 形式。

二维声波建模示例代码（见手册page27）：

% 创建计算网格
Nx = 128; % number of grid points in the x (row) direction
Ny = 256; % number of grid points in the y (column) direction
dx = 50e-6; % grid point spacing in the x direction [m]
dy = 50e-6; % grid point spacing in the y direction [m]
kgrid = makeGrid(Nx, dx, Ny, dy);


% 定义传播介质属性
medium.sound_speed = 1500*ones(Nx, Ny); % [m/s]
medium.sound_speed(1:50, :) = 1800; % [m/s]
medium.density = 1040; % [kg/m^3]


% 使用makeDisc函数定义输入源信号
disc_x_pos = 75; % [grid points]
disc_y_pos = 120; % [grid points]
disc_radius = 8; % [grid points]
disc_mag = 3; % [Pa]
source.p0 = disc_mag*makeDisc(Nx, Ny, disc_x_pos, disc_y_pos, disc_radius);


% 定义有50个阵元分布的环形笛卡尔传感器掩膜
sensor_radius = 2.5e-3; % [m]
num_sensor_points = 50;
sensor.mask = makeCartCircle(sensor_radius, num_sensor_points);

% 运行仿真
sensor_data = kspaceFirstOrder2D(kgrid, medium, source, sensor);

在上述代码中

kgrid：计算域被划分为 128 x 256 个网格点，网格点间距为 50 µm。

medium.speed：声速设置为异质（即不均匀）的，在域顶部附近速度更高。

source：源设置为圆盘形状的初始压力分布

sensor：传感器设置为具有 50 个传感器点的圆形阵列。

sensor.data = = kspaceFirstOrder2D(kgrid, medium, source, sensor);

四个输入结构体被传递给 kspaceFirstOrder2D，然后计算并返回在每个时间步长的每个传感器点记录的声压。结果返回到sensor.data结构体中。如下图所示

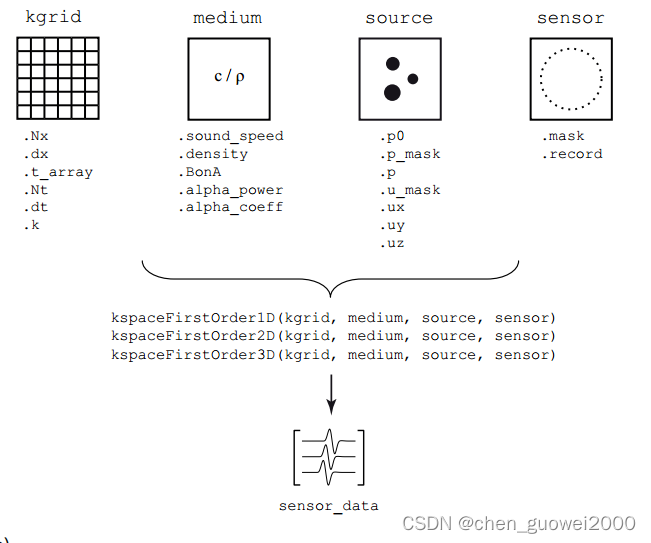
计算过程中图形界面如下图所示：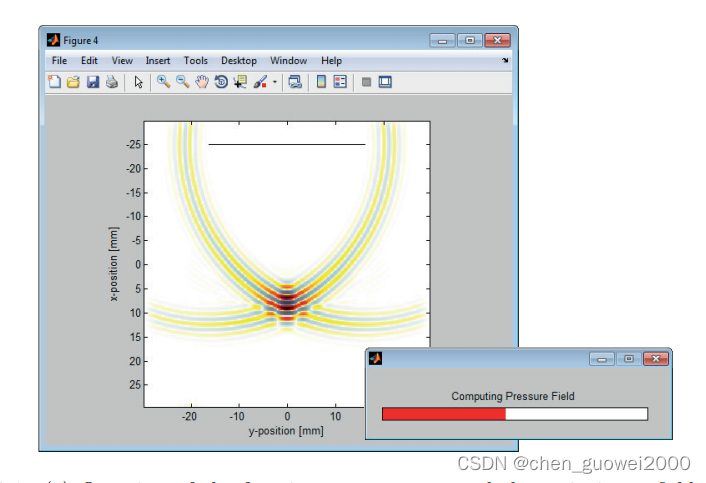

References

[1] B. E. Treeby and B. T. Cox, "k-Wave: MATLAB toolbox for the simulation and reconstruction of photoacoustic wave-fields," J. Biomed. Opt., vol. 15, no. 2, p. 021314, 2010. download pdf

[2] B. E. Treeby, J. Jaros, A. P. Rendell, and B. T. Cox, "Modeling nonlinear ultrasound propagation in heterogeneous media with power law absorption using a k-space pseudospectral method," J. Acoust. Soc. Am., vol. 131, no. 6, pp. 4324-4336, 2012. download pdf

[3] B. E. Treeby and B. T. Cox, "Modeling power law absorption and dispersion for acoustic propagation using the fractional Laplacian," J. Acoust. Soc. Am., vol. 127, no. 5, pp. 2741-2748, 2010. download pdf (see also 3.4 定义声源)